CBSE Class 9 - Mid-Point Theorem Videos
Mid Point Theorem
This video explains the Mid - Point theorem and its converse for a triangle and also solves problems based on these concepts.
More videos from this chapter
View All-
Types and Angle Sum Property
-
Types and Angle Sum Property
-
Types and Angle Sum Property
-
Parallelograms: Basic Properties
-
Problem solving on properties related to parallelogr ...
- the line segment joining the midpoints of two sides of a triangle is parallel to the third side
-
Q. 7
-
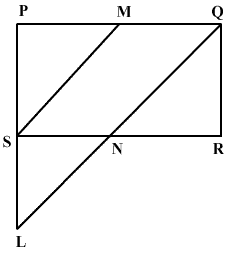
M is the mid point of side PQ of a parallelogram PQRS. A line through Q parallel to PS meets SR at N and PS produced at L. Prove that (i) PL = 2QR (ii) QL = 2QN.
- State the mid point Theorem.
- Prove that the triangles formed by joining in pairs, the mid points of the three sides of a triangle are congruent to each other.
- Prove that the line drawn through the mid point of one side of a triangle, parallel to another side, intersects the third side at its mid point.
-
In
PQR, A, B and C are the mid points of QR, RP and PQ respectively. If the lengths of sides PQ, QR and RP are 7 cm, 8 cm and 9 cm respectively, find the perimeter of ABC.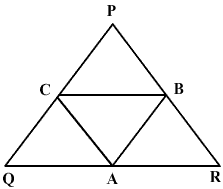 
- Prove that the triangle formed by joining the mid points of the sides of an isosceles triangle is an isosceles triangle.
-
In the figure, E is the mid-point of side AD of a trapezium ABCD with AB
CD. A line through E parallel to AB meets BC in F. Show that F is the mid point of BC.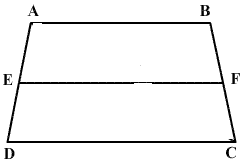 
-
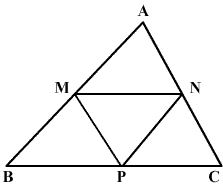
M, N and P are the mid points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm. Calculate BC, AB and AC.
