Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

Prove that the line drawn through the mid point of one side of a triangle, parallel to another side, intersects the third side at its mid point.
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
Expert Answer
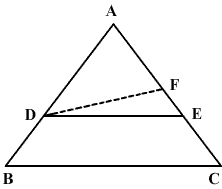
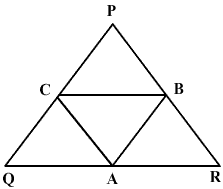
ABC is a triangle;
D is the mid point of AB.
To prove that E is the mid point of AC.
Let F be the mid point of the side AC and not the point E.
Join DF
In ABC, D is the mid point of AB and DE 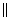 BC
F is the mid point of AC,
by mid point theorem,
DF 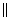 BC, also DE  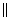BC
Thus two intersecting lines DE and DF are parallel to the same line BC
This is not possible.
So F can not be the mid point of AC.
Hence, E is the mid point of AC.
Answered by | 11 Aug, 2017, 02:00: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
the line segment joining the midpoints of two sides of a triangle is parallel to the third side
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
Q. 7
Asked by Rayeesa | 04 Jun, 2018, 09:58: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
M is the mid point of side PQ of a parallelogram PQRS. A line through Q parallel to PS meets SR at N and PS produced at L. Prove that (i) PL = 2QR (ii) QL = 2QN.
Asked by Topperlearning User | 11 Aug, 2017, 11:58: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
State the mid point Theorem.
Asked by Topperlearning User | 11 Aug, 2017, 12:01: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the triangles formed by joining in pairs, the mid points of the three sides of a triangle are congruent to each other.
Asked by Topperlearning User | 11 Aug, 2017, 11:59: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the line drawn through the mid point of one side of a triangle, parallel to another side, intersects the third side at its mid point.
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
In PQR, A, B and C are the mid points of QR, RP and PQ respectively. If the lengths of sides PQ, QR and RP are 7 cm, 8 cm and 9 cm respectively, find the perimeter of ABC. 
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the triangle formed by joining the mid points of the sides of an isosceles triangle is an isosceles triangle.
Asked by Topperlearning User | 11 Aug, 2017, 11:52: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
In the figure, E is the mid-point of side AD of a trapezium ABCD with AB  CD. A line through E parallel to AB meets BC in F. Show that F is the mid point of BC.
Asked by Topperlearning User | 11 Aug, 2017, 11:56: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
M, N and P are the mid points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm. Calculate BC, AB and AC.
Asked by Topperlearning User | 11 Aug, 2017, 11:59: AM
ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt