CBSE Class 10 - Areas of Combination of Figures Videos

• Please solve this question ?
  
• How to prove that opposite sides of a quadrilateral circumscribing a circle  subtend supplementary angles at the centre of the circle 
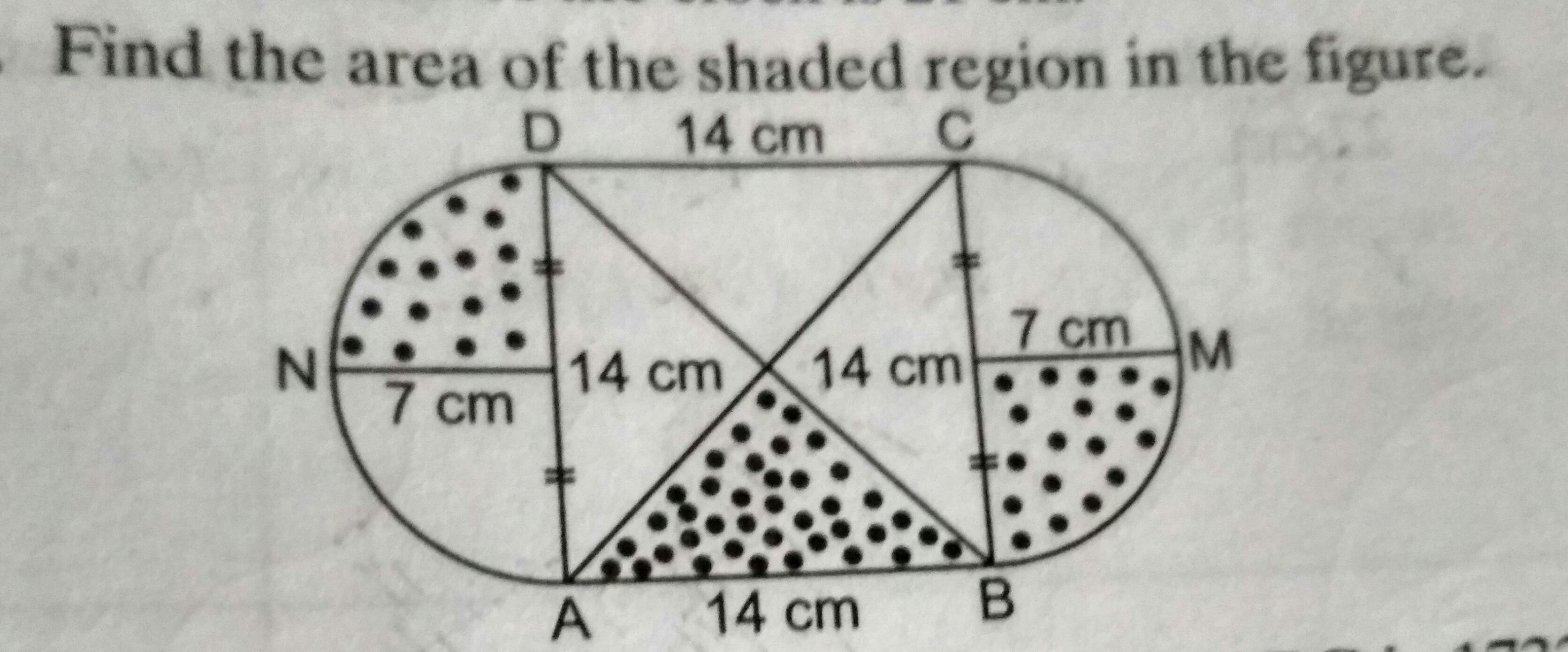
• Find area of shaded region
  
•  Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm 7 cm. Find the area of the remaining card board. Use pie=22/7
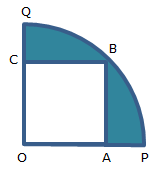
• In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region.
• The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semi-circles. If the track is 14 m wide every where, find the area of the track. Also, find the length of the outer boundary of the track.
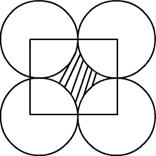
• Four equal circles are described about four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
• In triangle ABC, angle A = 90^o, AB = 12 cm and BC = 20 cm. Three semi-circles are drawn with AB, AC and BC as diameters. Find the area of the shaded portion.
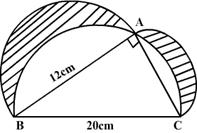
• In the figure, ABC is an equilateral triangle of side 12 cm. The circle is centered at A with radius 6 cm. Find the area of the shaded region.
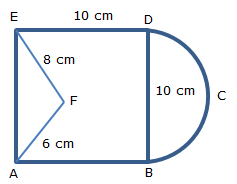
• Find the area of the region ABCDEFA shown in the figure, given that ABDE is a square of side 10 cm, BCD is a semi- circle with BD as diameter, EF = 8 cm, AF = 6 cm and angle AFE = 90^o.

Queries asked on Sunday & after 7 pm from Monday to Saturday will be answered after 12 pm the next working day.