CBSE Class 10 - Areas of Combination of Figures Videos
Shaded part
This video covers an application on areas related to circles
More videos from this chapter
View All-
Please solve this question ?

- How to prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle
-
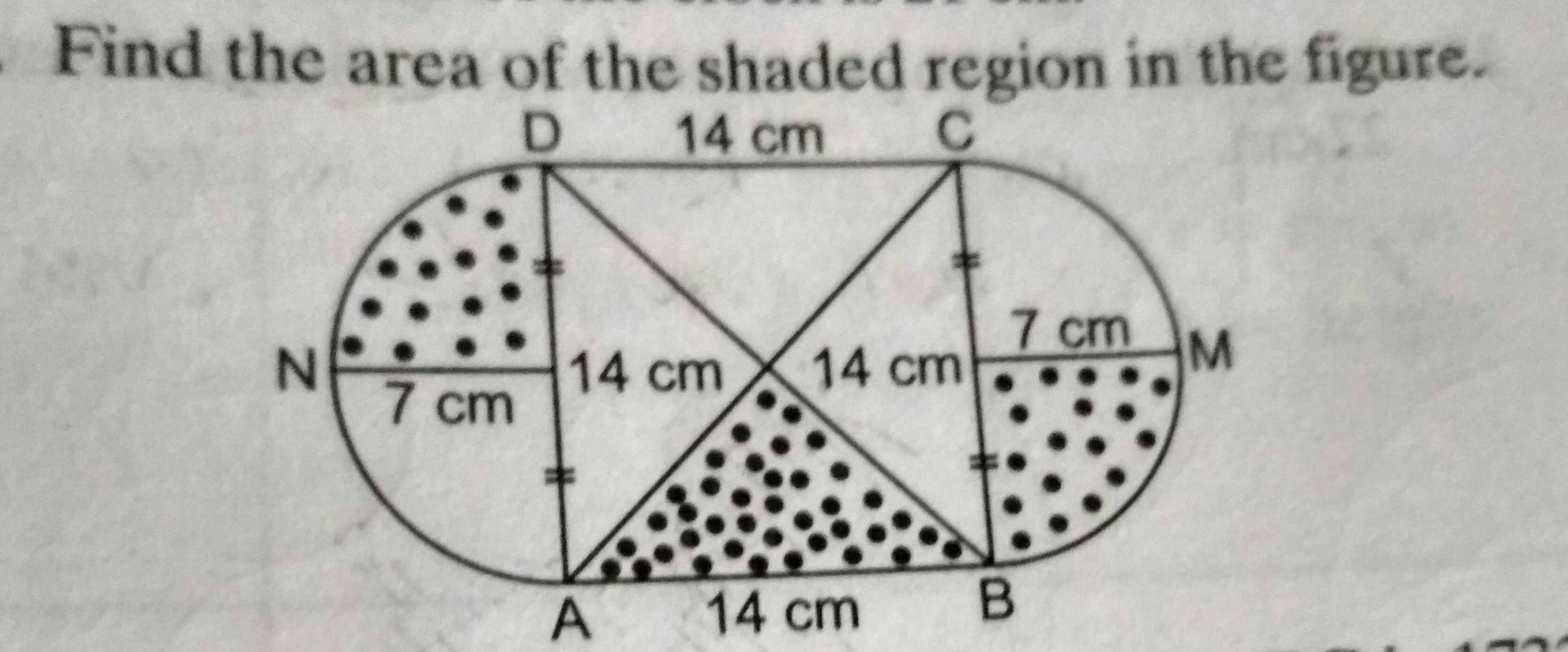
Find area of shaded region
- Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm 7 cm. Find the area of the remaining card board. Use pie=22/7
-
In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region.

-
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semi-circles. If the track is 14 m wide every where, find the area of the track. Also, find the length of the outer boundary of the track.

-
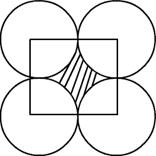
Four equal circles are described about four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
-
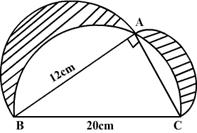
In triangle ABC, angle A = 90o, AB = 12 cm and BC = 20 cm. Three semi-circles are drawn with AB, AC and BC as diameters. Find the area of the shaded portion.
-
In the figure, ABC is an equilateral triangle of side 12 cm. The circle is centered at A with radius 6 cm. Find the area of the shaded region.
.jpg)
-
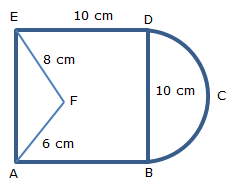
Find the area of the region ABCDEFA shown in the figure, given that ABDE is a square of side 10 cm, BCD is a semi- circle with BD as diameter, EF = 8 cm, AF = 6 cm and angle AFE = 90o.