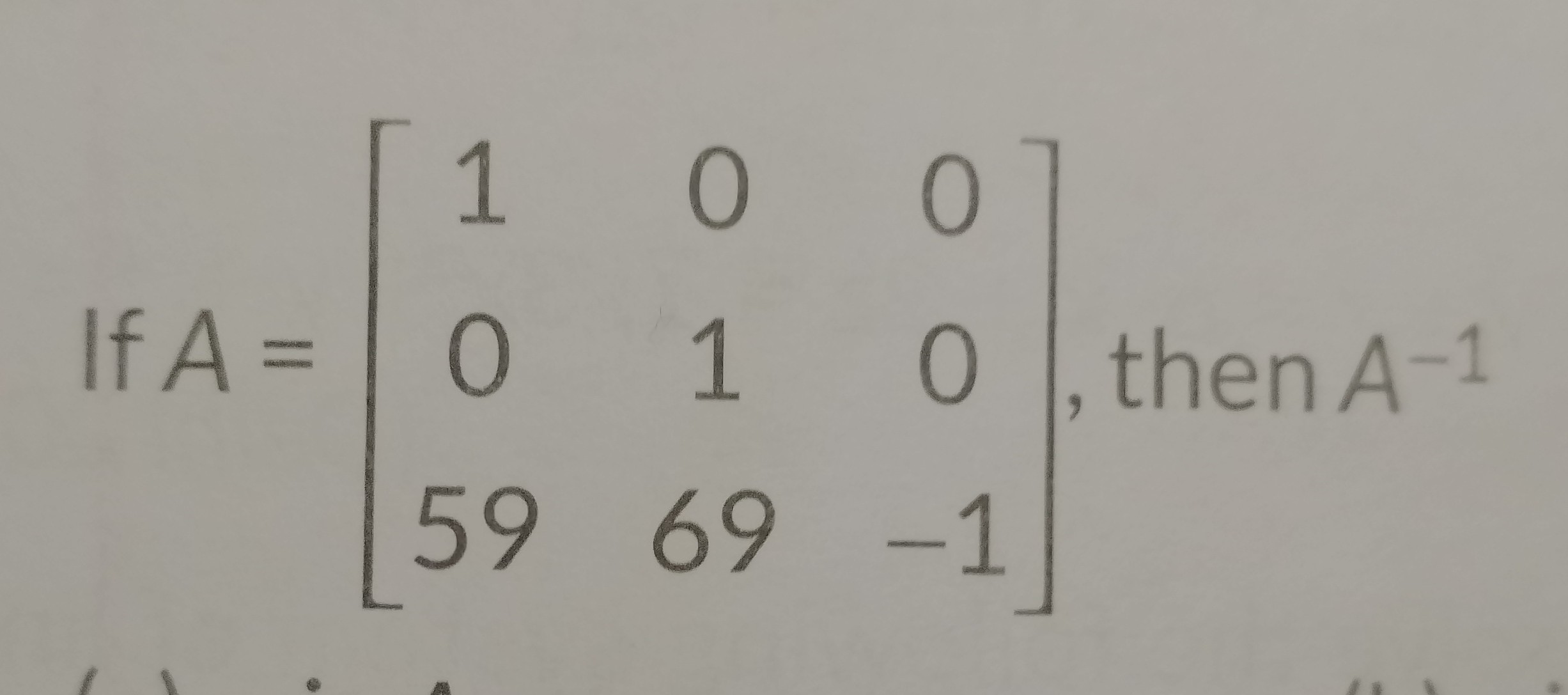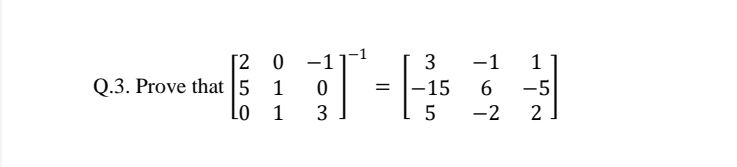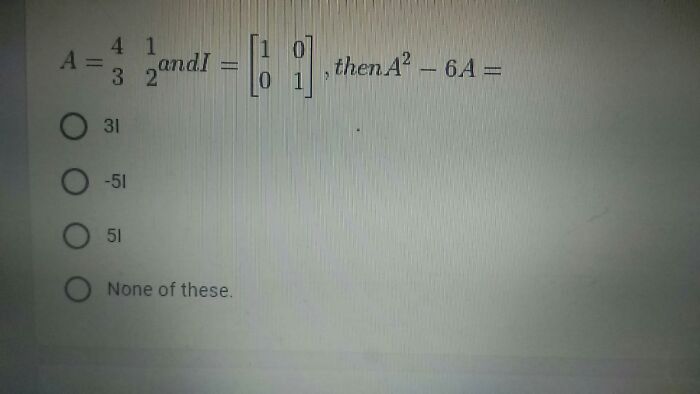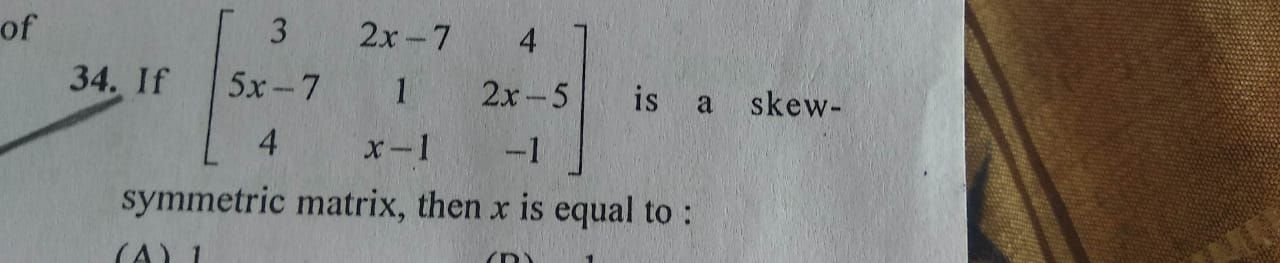CBSE Class 12-science Answered
why cant we divide a matrix
Asked by Pawan kalyan | 24 Apr, 2013, 05:14: PM
Expert Answer
The formal definition of division is actually given in terms of multiplication. a/b is defined to mean ab', where b' is the multiplicative inverse of b. The stuff the teach you early on in school about how division means "how many times one number goes into another number" is only the intuitive interpretation of division in the real numbers, and it makes no sense in other systems.
With this idea in mind, a logical matrix division A/B would be defined as AB^-1, where B^-1 is the inverse matrix of B. However, only square matrices with nonzero determinants have inverses, so this would be a very restricted operation. Fortunately, it doesn't matter. Division is only really a relevant operation in a field, and matrices pretty much never form a field, just vector spaces and modules.
With this idea in mind, a logical matrix division A/B would be defined as AB^-1, where B^-1 is the inverse matrix of B. However, only square matrices with nonzero determinants have inverses, so this would be a very restricted operation. Fortunately, it doesn't matter. Division is only really a relevant operation in a field, and matrices pretty much never form a field, just vector spaces and modules.
Answered by | 25 Apr, 2013, 07:07: AM
Concept Videos
-
Introduction to Matrices
This video explains what a matrix is, its order and discusses the types of ... -
Matrix Operations
This video explains addition of matrices, scalar multiplication of matrices... -
Concepts on Transpose of a matrix
Discuss Transpose of a matrix. Symmetric and Skew Symmetric matrices. Repre... -
Elementary operations
This video explains the elementary operations on matrices and how to apply ... -
Matrix and its order
Learn Matrix and its order. Discuss the types of matrices and equality of m...
CBSE 12-science - Maths
Asked by mahammadsharifdakhani67 | 16 Apr, 2024, 07:43: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by antra1799 | 18 Mar, 2024, 07:49: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by rahulsharmaaps4 | 03 Jan, 2023, 10:46: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by dakarapuaditya123 | 26 Dec, 2022, 08:20: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Shaikmahboob102003 | 29 Jun, 2022, 05:12: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by shivamaihar25 | 03 Jul, 2021, 10:33: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by cheragsaxena1607 | 26 Jun, 2021, 01:18: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by varunchauhan097 | 25 Apr, 2021, 08:09: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by yadavyogi294 | 07 Oct, 2020, 09:41: AM
ANSWERED BY EXPERT
