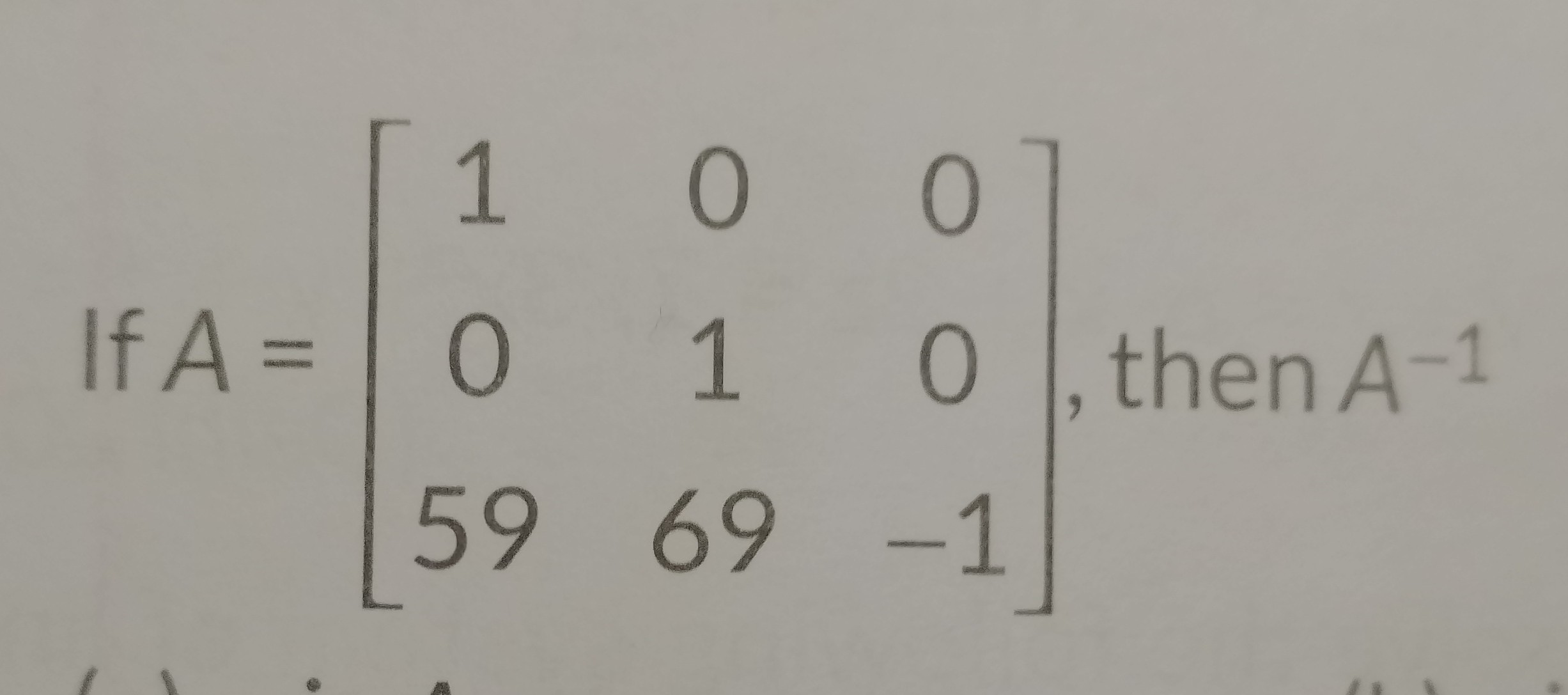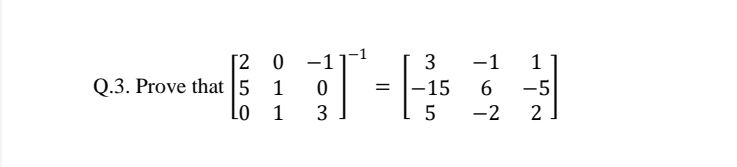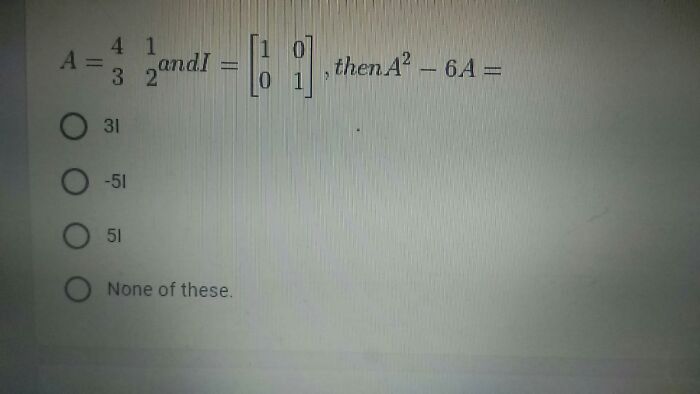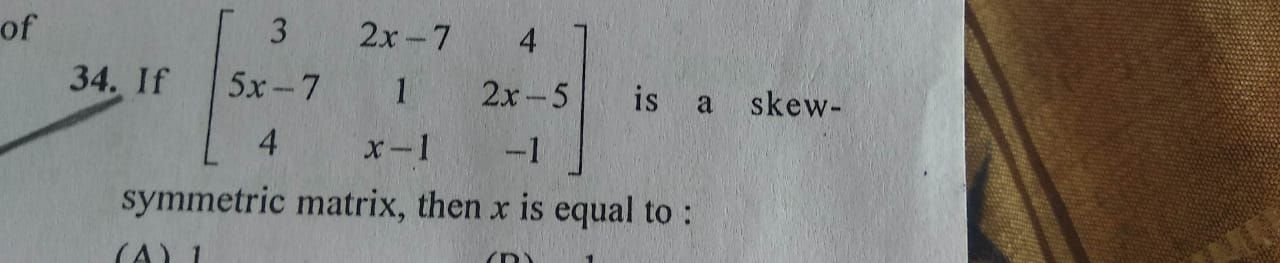CBSE Class 12-science Answered
When can we say a matrix is invertible?
Asked by Jogy Jacob | 05 Apr, 2013, 10:01: AM
Expert Answer
1. An n x n matrix A is called invertible if there exists an n x n matrix B such that AB = BA = I. In this case, B is called the inverse of A. A can only have an inverse if it is an n x n (square) matrix and the its determinant is not equal to 0.
2. In the above case, A would be the invertible marix i.e. the matrix of which inverse can be calculated and B would be the corresponding inverse matrix, i.e the matrix which is inverse of the invertible matrix.
3. Inverse of a matrix A = 1/determinant(A) * adj (A)
Answered by | 05 Apr, 2013, 04:51: PM
Concept Videos
-
Introduction to Matrices
This video explains what a matrix is, its order and discusses the types of ... -
Matrix Operations
This video explains addition of matrices, scalar multiplication of matrices... -
Concepts on Transpose of a matrix
Discuss Transpose of a matrix. Symmetric and Skew Symmetric matrices. Repre... -
Elementary operations
This video explains the elementary operations on matrices and how to apply ... -
Matrix and its order
Learn Matrix and its order. Discuss the types of matrices and equality of m...
CBSE 12-science - Maths
Asked by mahammadsharifdakhani67 | 16 Apr, 2024, 07:43: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by antra1799 | 18 Mar, 2024, 07:49: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by rahulsharmaaps4 | 03 Jan, 2023, 10:46: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by dakarapuaditya123 | 26 Dec, 2022, 08:20: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Shaikmahboob102003 | 29 Jun, 2022, 05:12: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by shivamaihar25 | 03 Jul, 2021, 10:33: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by cheragsaxena1607 | 26 Jun, 2021, 01:18: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by varunchauhan097 | 25 Apr, 2021, 08:09: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by yadavyogi294 | 07 Oct, 2020, 09:41: AM
ANSWERED BY EXPERT
