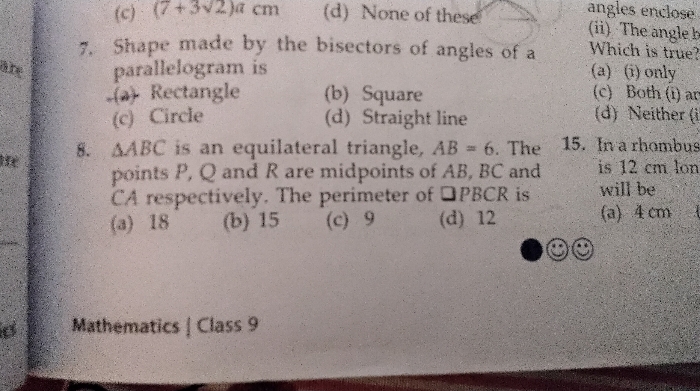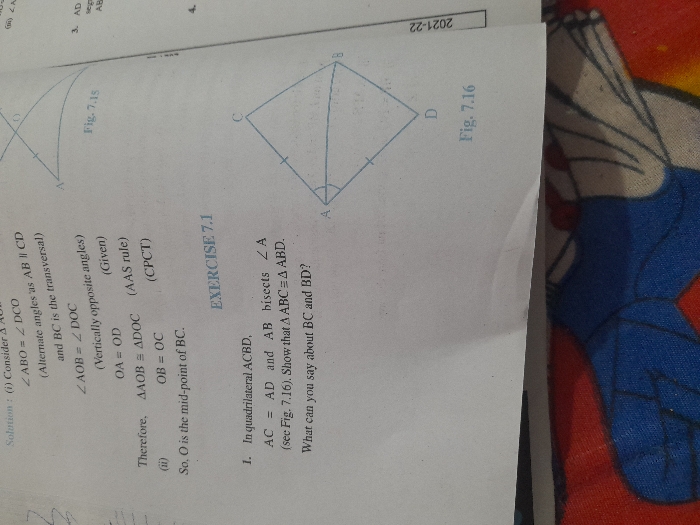
What is the maximum and minimum value of sin ? and cos ? ? Explain how.

Dear Student,

Properties Of The Sine Graph

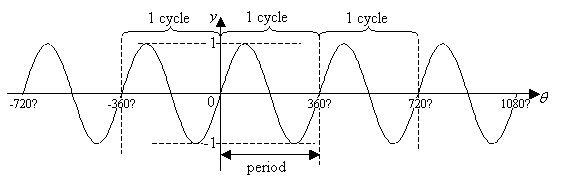
The sine function forms a wave that starts from the origin

• sin θ = 0 when θ = 0 ˚ , 180˚ , 360˚ .
• Maximum value of sin θ is 1 when θ = 90 ˚. Minimum value of sin θ is –1 when θ = 270 ˚. So, the range of values of sin θ is –1 ≤ sin θ ≤ 1.
• As the point θ moves round the unit circle in either the clockwise or anticlockwise direction, the sine curve above repeats itself for every interval of 360˚. The interval over which the sine wave repeats itself is called the period.

Properties Of The Cosine Graph

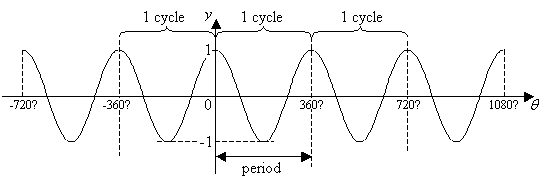
• The cosine function forms a wave that starts from the point (0,1)
• cos θ = 0 when θ = 90 ˚ , 270˚ .
• Maximum value of cos θ is 1 when θ = 0 ˚, 360˚. Minimum value of cos θ is –1 when θ = 180 ˚. So, the range of values of cos θ is – 1 ≤ cos θ ≤ 1.
• As the point P moves round the unit circle in either the clockwise or anticlockwise direction, the cosine curve above repeats itself for every interval of 360˚. Its period is 360˚.