CBSE Class 12-science Answered
What is the centre of mass of parabolic spandral ? Explain briefly with diagram
Asked by rushabhjain.a | 23 Oct, 2019, 07:16: PM
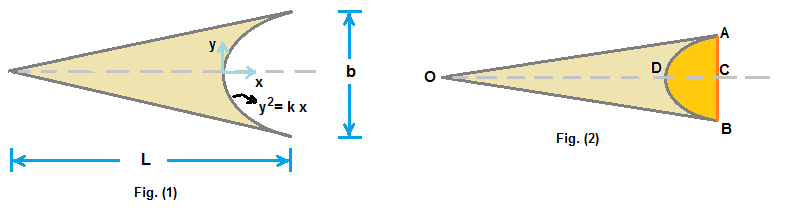
Fig.(1) shows the parabolic spandrel , which is a triangular plate cut at the base with parabolic curve as shown in figure.
Let us consider that we are given the dimensions, length L and width b . Curvature parameter k of parabolic curve y2 = k x is also known.
To get centre of mass (CM), let us consider area of spandrel is difference of area of triangle OAB and parabolic curve area ADB
By symmetry, CM is at axis of spandrel OD. Hence only we need to find the distance of CM from O.
Area of Triangle AT = (1/2) L b ;
Parabolic curve area from its length CD and known curve parameter k is calculated as follows
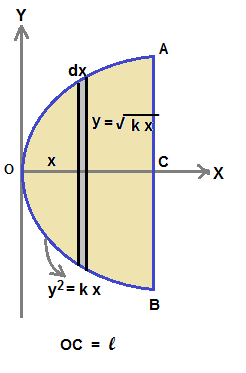
Area of parabola =  ...........................(1)
...........................(1)
 ...........................(1)
...........................(1)where l is length OC of parabolic curve area . In the given spandrel, we are given the length AC = b/2
OC and BC are related as AC2 = k OC or ( b2 / 4 ) = k l or l = b2/(4k) ...............(2)
using eqn.(2) , Area of parabola given in eqn.(1) is rewritten as ,
Area of parabola AP = (4/3) √k l3/2 = (4/3) √k [ b3 / (4k)3/2 ] = (1/6) ( b3 / k ) ....................(3)
Let x be the distance of CM (refer fig.(2) ) from point O
Then by taking moment of mass with respect to O, we have,
AS x + AP d = AT (2/3)L ..................(4)
where AS , AP and AT are area of spandrel, parabolic area and Triangle respectively.
d is distance of CM of parabolic area from O. For triangle, we consider CM is at a distance (2/3)L from O
Area of parabolic curve region AP is given in eqn.(3)
Area of spandrel AS = AT - AP = (1/2) L b - (1/6) ( b3 / k )
Centre of mass of parabolic area is (3/5) of its length from its apex point
( Refer answer for your previous question , CM of parabolic lamina )
Hence d , which is the distance of CM of parabolic area from O
d = OC - CD - (3/5) CD = OC - (2/5) CD = { L - [ b2 / (10k) ] }
Hence In eqn.(4), all values except x are known. Hence x cand be solved using eqn.(4)
I leave it to user to get the final answer by solving eqn.(4)
Answered by Thiyagarajan K | 24 Oct, 2019, 12:01: PM
Concept Videos
CBSE 12-science - Physics
Asked by ankush76728 | 05 May, 2024, 09:55: PM
CBSE 12-science - Physics
Asked by heymindurownbusiness | 04 May, 2024, 11:15: AM
CBSE 12-science - Physics
Asked by talulu | 01 May, 2024, 05:14: PM
CBSE 12-science - Physics
Asked by kanishkg511 | 30 Apr, 2024, 07:25: PM
CBSE 12-science - Physics
Asked by sahoobanita89 | 30 Apr, 2024, 05:10: AM
CBSE 12-science - Physics
Asked by divakar.9124 | 27 Apr, 2024, 10:42: PM
CBSE 12-science - Physics
Asked by panneer1766 | 24 Apr, 2024, 01:52: PM
CBSE 12-science - Physics
Asked by artabandhusahu85 | 24 Apr, 2024, 12:07: PM
CBSE 12-science - Physics
Asked by niharvijayvargiya5 | 23 Apr, 2024, 06:40: PM