Ask a Doubt

Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

To Prove:

a cosA+b cosB+c cosC=2 sin B sin C

Asked by prasantaratha.lic | 24 Nov, 2016, 10:46: AM

Expert Answer

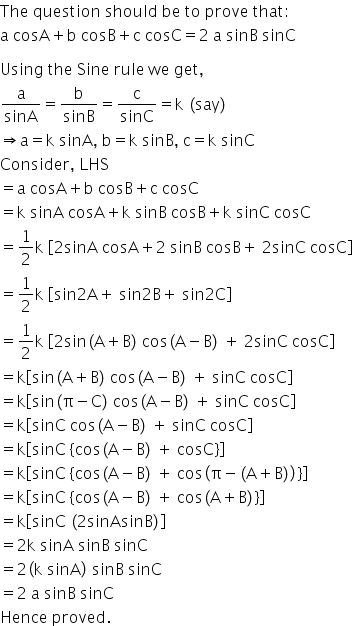
begin mathsize 16px style The space question space should space be space to space prove space that colon straight a space cosA plus straight b space cosB plus straight c space cosC equals 2 space straight a space sinB space sinC Using space the space Sine space rule space we space get comma straight a over sinA equals straight b over sinB equals straight c over sinC equals straight k space left parenthesis say right parenthesis rightwards double arrow straight a equals straight k space sinA comma space straight b equals straight k space sinB comma space straight c equals straight k space sinC Consider comma space LHS equals straight a space cosA plus straight b space cosB plus straight c space cosC equals straight k space sinA space cosA plus straight k space sinB space cosB plus straight k space sinC space cosC equals 1 half straight k space open square brackets 2 sinA space cosA plus 2 space sinB space cosB plus space 2 sinC space cosC close square brackets equals 1 half straight k space open square brackets sin 2 straight A plus space sin 2 straight B plus space sin 2 straight C close square brackets equals 1 half straight k space open square brackets 2 sin left parenthesis straight A plus straight B right parenthesis space cos left parenthesis straight A minus straight B right parenthesis space plus space 2 sinC space cosC close square brackets equals straight k open square brackets sin left parenthesis straight A plus straight B right parenthesis space cos left parenthesis straight A minus straight B right parenthesis space plus space sinC space cosC close square brackets equals straight k open square brackets sin left parenthesis straight pi minus straight C right parenthesis space cos left parenthesis straight A minus straight B right parenthesis space plus space sinC space cosC close square brackets equals straight k open square brackets sinC space cos left parenthesis straight A minus straight B right parenthesis space plus space sinC space cosC close square brackets equals straight k open square brackets sinC space open curly brackets cos left parenthesis straight A minus straight B right parenthesis space plus space cosC close curly brackets close square brackets equals straight k open square brackets sinC space open curly brackets cos left parenthesis straight A minus straight B right parenthesis space plus space cos open parentheses straight pi minus left parenthesis straight A plus straight B right parenthesis close parentheses close curly brackets close square brackets equals straight k open square brackets sinC space open curly brackets cos left parenthesis straight A minus straight B right parenthesis space plus space cos left parenthesis straight A plus straight B right parenthesis close curly brackets close square brackets equals straight k open square brackets sinC space left parenthesis 2 sinAsinB right parenthesis close square brackets equals 2 straight k space sinA space sinB space sinC equals 2 open parentheses straight k space sinA close parentheses space sinB space sinC equals 2 space straight a space sinB space sinC Hence space proved. end style

Answered by Rebecca Fernandes | 24 Nov, 2016, 02:46: PM

Practice Test

Answered Unanswered My Questions My Answers

CBSE 11-science - Maths

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

A n space a i r c r a f t space t r a c k i n g space s t a t i o n space d e t e r m i n e s space t h e space d i s tan c e space f r o m space a space c o m m o n space p o i n t space O t o space e a c h space a i r c r a f t space a n d space t h e space a n g l e space b e t w e e n space t h e space a i r c r a f t s. I f space a n g l e space O space b e t w e e n space t h e space t w o space a i r c r a f t s space i s space 49 to the power of 0 a n d space t h e space d i s tan c e space f r o m space p o i n t space O space t o space t h e space t w o space a i r c r a f t s space a r e space 50 k m space a n d space 72 k m comma f i n d space t h e space d i s tan c e space b e t w e e n space t h e space t w o space a i r c r a f t s ?

Asked by Topperlearning User | 31 Aug, 2016, 10:16: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

Asked by Topperlearning User | 31 Aug, 2016, 10:29: PM

ANSWERED BY EXPERT

CBSE 11-science - Maths

Asked by Topperlearning User | 31 Aug, 2016, 10:40: PM

ANSWERED BY EXPERT

My Class Videos Tests Plans Ask a Doubt

Get Latest Study Material for Academic year 24-25 Click here

×