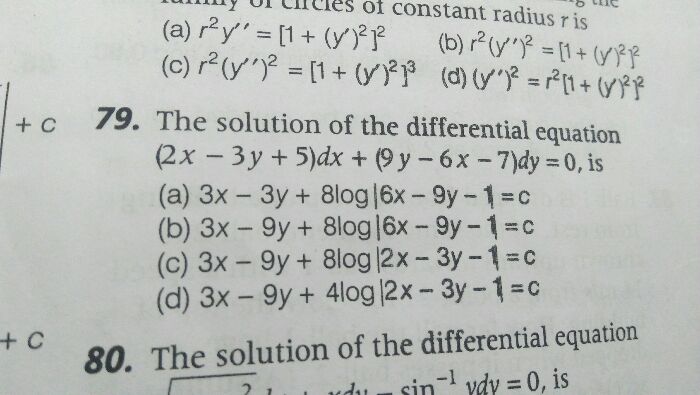CBSE Class 12-science Answered
the solution
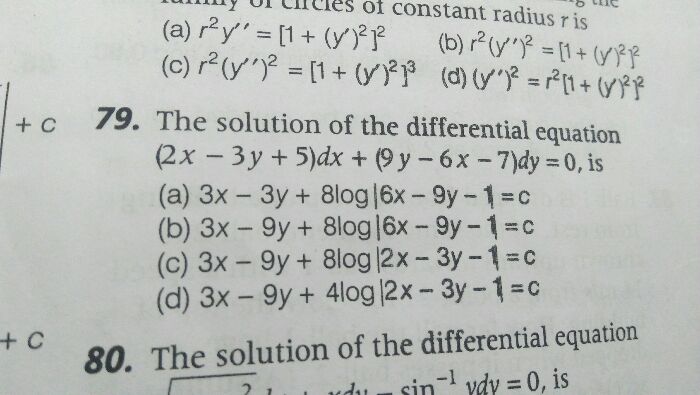
Asked by reddyanji405 | 05 Jun, 2020, 10:29: AM
To find the solution of the differential equation: (2x - 3y + 5)dx + (9y - 6x -7)dy = 0
This can be done as follows:
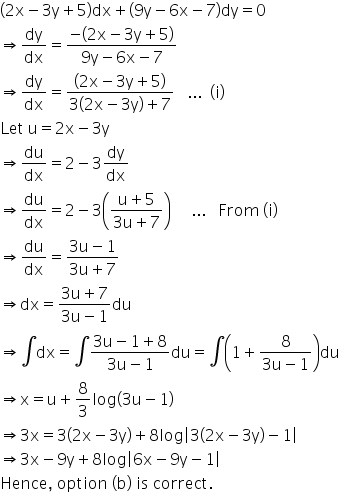
Answered by Renu Varma | 05 Jun, 2020, 12:58: PM
Concept Videos
CBSE 12-science - Maths
Asked by aishaazmata | 24 Apr, 2024, 20:48: PM
CBSE 12-science - Maths
Asked by arunabhapaul123 | 25 Jan, 2022, 14:13: PM
CBSE 12-science - Maths
Asked by reddyanji405 | 05 Jun, 2020, 10:29: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM