CBSE Class 9 Answered
The sides AB and AC of a triangle are produced to D and E respectively. The bisectors of  CBD and
CBD and  BCE meet at O. If
BCE meet at O. If  A = 40o, find
A = 40o, find  BOC.
BOC.
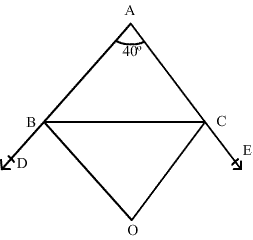

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
![]() B+
B+ ![]() CBD= 180o (linear pair)
CBD= 180o (linear pair)
Similarly,  BCO = 90o -
BCO = 90o -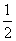
 C
C
In  OBC,
OBC,  CBO +
CBO +  BCO +
BCO +  BOC = 180o (angle sum of a
BOC = 180o (angle sum of a )
)
(90o -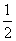
 B) + (90o -
B) + (90o -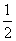
 C) +
C) +  BOC = 180o
BOC = 180o
Answered by | 04 Jun, 2014, 03:23: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by raghavgargrg28 | 10 Sep, 2021, 05:11: PM
CBSE 9 - Maths
Asked by kamateganpati | 08 Sep, 2021, 06:17: PM
CBSE 9 - Maths
Asked by swatipuspapatel | 07 Feb, 2021, 07:29: PM
CBSE 9 - Maths
Asked by sanjanatirthani0574 | 12 Sep, 2020, 10:18: AM
CBSE 9 - Maths
Asked by Tanushkadari456 | 22 Sep, 2019, 05:50: PM
CBSE 9 - Maths
Asked by Santosh.kumar0317 | 19 Aug, 2019, 05:12: PM
CBSE 9 - Maths
Asked by Chetna.lagoon | 18 Aug, 2019, 07:32: PM
CBSE 9 - Maths
Asked by Girishdhawan | 01 Jul, 2018, 03:13: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM