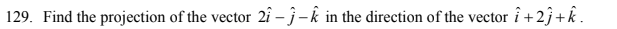CBSE Class 12-science Answered
The position vectors of A, B and C are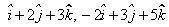 
and 
. Prove that A, B and C are collinear.
and 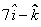. Prove that A, B and C are collinear.
Asked by Topperlearning User | 03 Mar, 2015, 01:45: PM
Expert Answer
Here, we have
Since,
, therefore 
are parallel, but B is the common point in both the vectors. Thus, A, B and C are collinear.
, therefore 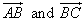are parallel, but B is the common point in both the vectors. Thus, A, B and C are collinear.
Answered by | 03 Mar, 2015, 03:45: PM
Concept Videos
-
Vector multiplication concepts
Multiplication of a vector by a scalar, vector joining two points. Directio... -
Concepts and application on properties of vector ...
Multiplication of a vector by a scalar, vector joining two points. Directio... -
Properties of Vectors
Multiplication of a vector by a scalar, vector joining two points. Directi...
CBSE 12-science - Maths
Asked by durgaprasaddurgaprasad174 | 01 Jul, 2022, 05:05: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by abhimeena1011 | 18 Jan, 2022, 10:43: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by haroonrashidgkp | 23 Oct, 2018, 07:06: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by akshitaasia | 19 Mar, 2018, 11:04: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 13 Aug, 2016, 02:21: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
, then find the value of 
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
is an isosceles.Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 03 Mar, 2015, 01:45: PM
ANSWERED BY EXPERT
