CBSE Class 10 Answered
show that a number and its cube leaves the same remainder when divided by 6
Asked by | 08 Mar, 2009, 10:29: AM
Suppose a number a is divided by 6 gives a quotient q and remainder r, then we can write,
a=6q+r where r is an integer such that ![]()
so r takes the values 0,1,2,3,4 and 5.
we see that cube of each of these numbers leaves a remainder equal to the number itself, when divided by 6.
So,
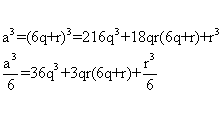
We see that each of the terms except the last one is a multiple of 6.
In the last term we'll get some quotient say t and a remainder equal to r( as mentioned above)
Hence the answer.
Answered by | 08 Mar, 2009, 12:21: PM
CBSE 10 - Maths
Asked by KONDA VENKATA KHEERTHANA | 04 May, 2018, 10:29: AM
CBSE 10 - Maths
Show that every positive even integer is of the form2q and every positive odd integer is of the form
Asked by suryap2 | 26 May, 2010, 04:16: PM
CBSE 10 - Maths
Asked by surazz | 23 May, 2010, 12:31: PM
CBSE 10 - Maths
Asked by sahil.95rana | 23 May, 2010, 06:53: AM
CBSE 10 - Maths
Asked by surazz | 09 May, 2010, 10:06: AM
CBSE 10 - Maths
Asked by sumandeesinghrana | 30 Apr, 2010, 08:15: PM
CBSE 10 - Maths
Asked by ayushikas | 30 Apr, 2010, 08:42: AM
CBSE 10 - Maths
Asked by saraza | 27 Apr, 2010, 08:55: PM
CBSE 10 - Maths
Asked by kanz_daruler1 | 26 Apr, 2010, 09:52: PM

