Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

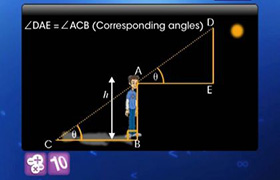
Rodney stood 30 m away from the light house in such a way that the angle of elevation of the top of the light house from his eyes was 45º. Rodney"s height is  1.4 m. Find the height of the light house.
Asked by Topperlearning User | 02 Nov, 2017, 09:36: AM
answered-by-expert Expert Answer
 
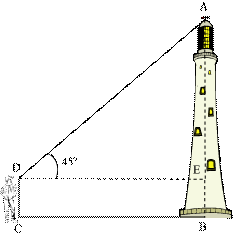
Here, AB is the light house and CD is the observer, Rodney.
 
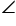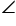The angle of elevation is represented by angleADE.
 
Hence, we can see that in this case, ADE is a triangle, right angled at E and we are required to find out the height of the light house.
 
 
We have       AB = AE + BE
                     AB = AE + 1.4
And              DE = CB = 30 m
 
Now, to determine AE, we choose a trigonometric ratio that involves both AE and DE.
 
Let us choose the tangent of the angle of elevation.
 
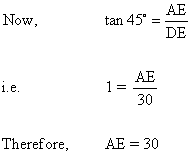
So, the height of the light house (AB) = (30 + 1.4) m = 31.4 m
Answered by | 02 Nov, 2017, 11:36: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
Two buildings face each other. The height of one building is greater than that of the other. The smaller building is 80 m high. The angles of depression of the top and the bottom of the smaller building from the top of the taller building are 45º and 60º respectively. Find the height of the taller building.
Asked by shanbhog.06 | 14 Apr, 2022, 11:26: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
In triangle ABC, AD is perpendicular to BC, angles B and C are of measures 30 and 60 respectively, if AD=7m, then find the value og BC.
Asked by godboletanaya | 24 Dec, 2021, 11:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
cos theta +cos theta is equal to
Asked by nikunjgupta102021 | 12 Jul, 2021, 09:01: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
what is different between height and distance
Asked by onkarmishra074 | 17 May, 2020, 02:52: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
A tower stands vertically on the ground.from a point which is15 Meyer away from the foot of the tower , the angle of elevation of the top of the tower is 45 degree . what is the height of the tower?
Asked by udaya2885 | 04 Jan, 2020, 10:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Two buildings face each other. The height of one building is greater than that of the other. The smaller building is 80 m high. The angles of depression of the top and the bottom of the smaller building from the top of the taller building are 45º and 60º respectively. Find the height of the taller building.
Asked by Topperlearning User | 02 Nov, 2017, 09:19: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
A tree is broken by the wind. The top struck the ground at an angle of 30o and at a distance of 30 metres from the root. Find the whole height of the tree.
Asked by Topperlearning User | 02 Nov, 2017, 09:26: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
John stands on the bridge and observes that the angles of depression of the banks on opposite sides of river Absyssa are 45º and 60º respectively. The bridge is at a height of 6 m from the banks. Calculate the width of the river Absyssa?
Asked by Topperlearning User | 02 Nov, 2017, 09:34: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Rodney stood 30 m away from the light house in such a way that the angle of elevation of the top of the light house from his eyes was 45º. Rodney"s height is  1.4 m. Find the height of the light house.
Asked by Topperlearning User | 02 Nov, 2017, 09:36: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The angle of elevation of the top of a tower from a point A on the ground is 30o. On moving a distance of 20 metres towards the foot of the tower to a point B the angle of elevation increases to 60o. Find the height of the tower and distance of the tower from the point A.
Asked by Topperlearning User | 02 Nov, 2017, 09:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×