CBSE Class 10 Answered

Dear Student,

However its unclear in the question, as to which 'given proof ' is referred to, still, We are giving the following two proofs of Pythagoras Theorem:

The Pythagoras Theorem says, that for a right triangle, with hypotenuse 'c', and legs 'a' and 'b',

c²=a²+b²

PROOF#1. In order to prove the theorem, we construct squares on each of the sides of the triangle:

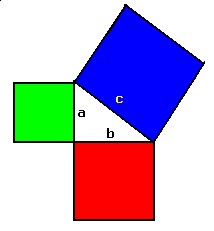
If we can show that the area of the green square plus the area of the red square is equal to the area of the blue square, then we have proven the Pythagorean Theorem.

Now let's draw a line extending the 'a' side and a line extending the 'b' side.  Then we draw 2 lines perpindicular to these lines so that the blue square is surrounded by a larger square each side having a length of (a+b). Therefore, the area of the larger square equals (a+b)² which equals a² + 2ab + b².

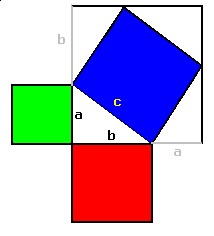
Note that the blue square is surrounded by 4 right triangles, the area of each being ½ (a•b) and so the area of all 4 triangles totals 2•a•b.
So, the area of the blue square = area of the surrounding square minus the area of the 4 triangles.

PROOF#2:

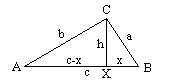
The simplest proof is an algebraic proof using similar triangles ABC, CBX, and ACX (in the diagram):

Since corresponding parts of similar triangles are proportional,

      a/x=c/a 

=> a²=cx.

And b/(c-x)=c/b 

=>   b²=c²-cx

=>   c²=cx+b².

Substituting a² for cx, we get,

c²=a²+b²

Hence Proved.

Regards Topperlearning.