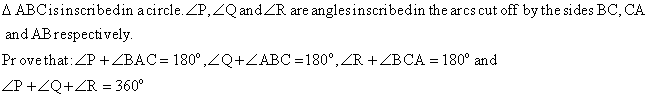CBSE Class 9 Answered
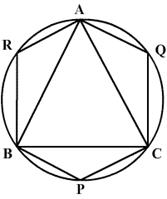
Prove that the quadrilateral formed by the bisectors of internal angles of a cyclic quadrilateral is also cyclic.
Asked by Topperlearning User | 04 Oct, 2017, 14:03: PM
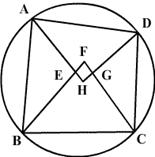

Answered by | 04 Oct, 2017, 16:03: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by sdmbotch1123 | 17 Dec, 2022, 21:39: PM
CBSE 9 - Maths
Asked by nirup6957 | 20 Jan, 2020, 19:10: PM
CBSE 9 - Maths
Asked by mukhreetyadav1972 | 29 Dec, 2019, 19:34: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Oct, 2017, 14:06: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Oct, 2017, 14:03: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Oct, 2017, 13:55: PM







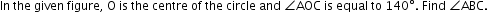
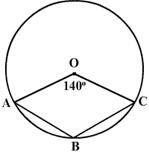
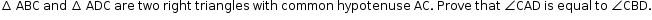
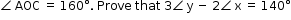 .
.