CBSE Class 9 Answered
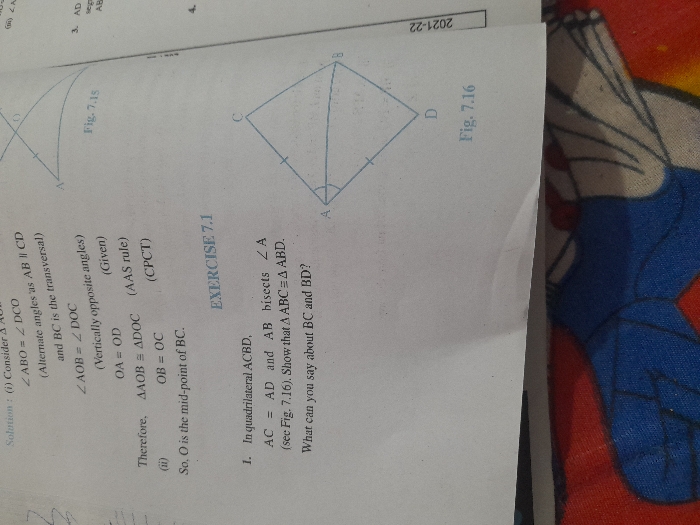
prove that: (i)If all medians of a triangle are equal then triangle is equilateral.
(ii)sum of any two medians of a triangle is greater than the third median.
Asked by araima2001 | 10 Sep, 2014, 08:36: PM
(i)
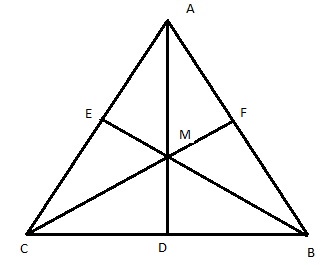
Let ABC be a triangle and our medians AD, BE and CF, where D is the mid-point of AB, E is the midpoint of AC and F is the midpoint of AB.
Let us say all the medians intersect at the point M, which would make M the centroid of our triangle ABC.
Now a centroid divides each median in the ratio 2:1. So we now have
AM:MD = BM:ME = CM:MF = 2:1
Let us say all the medians intersect at the point M, which would make M the centroid of our triangle ABC.
Now a centroid divides each median in the ratio 2:1. So we now have
AM:MD = BM:ME = CM:MF = 2:1
The question says that the medians are equal in length. So let us say AM = BM = CM = 2 units and MD = ME = MF = 1 unit.
Now consider the triangles, CDM and AFM. They can be proved to be congruent, because the CM = AM, FM = MD and the angle between AMF = angle between CMD. Now since these triangles are congruent, AF = CD.
But F is the mid-point of AB, so AF = FB. So we just proved AF = FB = BD = CD.
Hence, AF + FB = BD + CD. And hence, AB = BC.
You can prove similarly for the side AC and AB too and show that BC = AC, effectively proving that AB = BC = AC and hence its an equilateral triangle.
Now consider the triangles, CDM and AFM. They can be proved to be congruent, because the CM = AM, FM = MD and the angle between AMF = angle between CMD. Now since these triangles are congruent, AF = CD.
But F is the mid-point of AB, so AF = FB. So we just proved AF = FB = BD = CD.
Hence, AF + FB = BD + CD. And hence, AB = BC.
You can prove similarly for the side AC and AB too and show that BC = AC, effectively proving that AB = BC = AC and hence its an equilateral triangle.
Answered by Prasenjit Paul | 11 Sep, 2014, 11:08: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by borakartike2 | 29 Dec, 2023, 09:21: PM
CBSE 9 - Maths
Asked by ghodage | 12 Dec, 2023, 07:23: PM
CBSE 9 - Maths
Asked by vijaykasaudhan913 | 10 Dec, 2023, 04:40: PM
CBSE 9 - Maths
Asked by aksharapatni | 30 Nov, 2023, 01:12: PM
CBSE 9 - Maths
Asked by rajetigirija | 19 Nov, 2023, 08:11: AM
CBSE 9 - Maths
Asked by Krishna962511 | 23 Jan, 2023, 10:41: AM