CBSE Class 10 Answered
Prove that : √2+tan2 θ+cot2 θ=tan θ+cot θ
Asked by harshrajesh9 | 28 Jul, 2020, 12:52: PM
To prove: √(2+tan2θ+cot2θ) = tan θ+cot θ
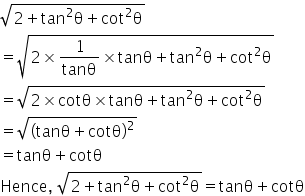
Answered by Renu Varma | 28 Jul, 2020, 19:40: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by syashkurun | 08 Jul, 2024, 19:14: PM
CBSE 10 - Maths
Asked by pm86982 | 10 Apr, 2023, 12:24: PM
CBSE 10 - Maths
Asked by adinaditi29 | 14 Mar, 2022, 12:02: PM
CBSE 10 - Maths
Asked by ambarishpatil7 | 28 Sep, 2021, 20:49: PM
CBSE 10 - Maths
Asked by manish.mayuka | 02 May, 2021, 14:02: PM
CBSE 10 - Maths
Asked by abhishekmonupatel27 | 23 Feb, 2021, 16:31: PM
CBSE 10 - Maths
Asked by pramoddomarp121 | 26 Sep, 2020, 18:01: PM














