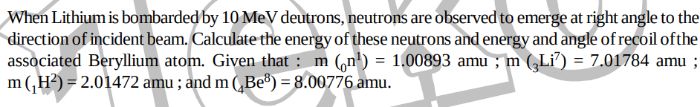Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

pls solve
question image
Asked by swayamagarwal2114 | 21 Jul, 2022, 17:17: PM
answered-by-expert Expert Answer
If the energy of incident deutron  is 10 MeV, then we get speed u of deutron from the following expression
 
Ek = (1/2) m u2
 
where m is mass of deutron
 
begin mathsize 14px style u space equals space square root of fraction numerator 2 space E over denominator m end fraction end root space equals space square root of fraction numerator 2 cross times 10 cross times 1.602 space cross times 10 to the power of negative 13 end exponent over denominator 2.01472 space cross times space 1.66 space cross times space 10 to the power of negative 27 end exponent end fraction end root space equals space 3.095 space cross times space 10 to the power of 7 space m divided by s end style
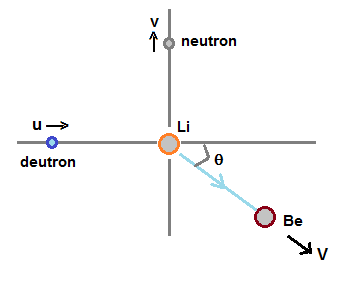
As shown in figure , let us assume deutron incident along x-axis direction with velocity u on a
Li nucleus which is at rest . The collision makes a following nuclear reaction.
 
begin mathsize 14px style D presubscript 1 presuperscript 2 space plus space L presubscript 3 presuperscript 7 i space rightwards arrow B presubscript 4 presuperscript 8 e plus n presubscript 0 presuperscript 1 end style
 
 
hence , at end of nuclear reaction, we get Be and neutron. Neutron is moving with velocity v along y-axis.
Let Be moves with velocity V in a direction that makes angle θ with x-axis as shown in figure.
 
Total mass before collision = ( 2.01472 + 7.01784 ) amu = 9.03256 amu
Total mass after  collision  = ( 1.00893 + 8.00776 ) amu = 9.01669 amu
 
Tha mass difference Δm is converted into energy of nuclear reaction , E = Δm c2 , where c is speed of light 
 
Δm = 1.587 × 10-2 amu   ;   E = ( 1.587 × 10-2 × 931.5 ) MeV = 14.783 MeV = 2.368 × 10-12 J
 
( Conversion factors used abve :-   1 amu = 931.5 MeV , 1 MeV = 1.602 × 10-13 J )
 
Collision is super elastic collision because energy is increased after collision .
 
By momenum conservation ,  md u = mBe Vx
 
where md is mass of deutron , mBe is mass of Be nucleus and Vx is x-component of velocity of Be nucleus
 
Vx = ( md / mBe ) u  = ( 2.01472 / 8.00776 ) × 3.095 × 107  m/s
 
Vx = 7.787 × 106 m/s   .................................(1)

By momenum conservation ,  mn v = mLi Vy
 
Hence speed of neutron v = ( mLi / mn ) Vy  = ( 7.01784 / 1.00893 ) Vy
 
speed of neutron v = 6.9557 Vy ..............................(2)
 
If energy released from nuclear reaction appears in the form of kinetie energies of neutron and Be nucleus,
then we have
 
(1/2) mn v2 + (1/2) mBe Vx2 + (1/2) mBe Vy2  = 2.368 × 10-12 J
 
By substituting Vx from eqn.(1) and substituting v from eqn.(2) ,
we get from above expression ,  Vy = 6.455 × 106 m/s
 
from eqn.(2) , speed of neutron v = 4.515 × 107 m/s
 
Velocity of Be nucleus = begin mathsize 14px style square root of V subscript x superscript 2 space plus space V subscript y superscript 2 end root space end style= 1.011 × 108 m/s
Angle made by the direction of Be nucleus with x-axis ,  tan-1 ( 6.455 / 7.787 ) =39.6o ( clockwise direction )
Answered by Thiyagarajan K | 22 Jul, 2022, 10:58: AM
Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
A ball of mass m approaches a moving wall of infinite mass with speed v along the normal to the wall. The speed of the ball is u towards the ball. The speed of the ball after elastic collision with the wall is
Asked by yayashvadutta45 | 15 Sep, 2024, 19:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
the block of mass M moving on the frictionless horizontal surface collides with the spring of spring constant K and compresses it by length l.the maximum momentum of the body after collision is
Asked by karripaparao74 | 20 Aug, 2024, 23:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Help me
question image
Asked by nandichandi33 | 24 Mar, 2024, 21:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
The work done in moving a body of mass m up an inclined plane of inclination ? to the horizontal, height h and length l ( no friction ) are related as
Asked by sarthakbhoskar7630 | 05 Mar, 2024, 19:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
A uniform rod of length L and mass M has been placed on a rough horizontal surface. The force F applied on the rod is such that the rod is such that the rod is just in the state of rest. If the coefficient of friction varies according to the relation μ=KX, where K is a positive constant. Suppose friction is present only from X=0 to X=L. If the rod moves in the direction of application of force then the total heat generated in the time in which the rod crosses this region, is equal to
Asked by fekishfaker | 18 Nov, 2023, 13:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
A wooden block weighing 80 N rests on a rough horizontal plane, the coefficient of friction between the two being µ=0.4. If a bullet weighing 0.4 N is fired horizontally in to the block with muzzle velocity v= 500 m/s, how far will the block be displaced from its initial position? Assume that the bullet remains inside the block.
Asked by theavengers0203 | 24 May, 2023, 08:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
law of conservation of energy in case of freely falling body
Asked by mdowaisraza581 | 16 May, 2023, 22:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
solve question
question image
Asked by rasjad355 | 15 Jan, 2023, 16:49: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
pls solve
question image
Asked by swayamagarwal2114 | 21 Jul, 2022, 17:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Two block A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length as shown in fig. A third identical block C, also of mass m, moving on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
question image
Asked by vishal.vini86 | 22 Apr, 2022, 00:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt