JEE Class main Answered

If plancks constant h, speed of light c and universal gravitational constant G are combined to form the unit of mass ,
then we have
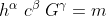 \ \ ................................(1)
\ \ ................................(1)
where m is mass . 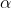 ,
, 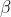 and
and 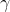 are constants to be determined by using dimensional analysis.
are constants to be determined by using dimensional analysis.
SI unit of planck constant h = J s = N m s = kg m s-2 m s
Hence dimension of planck's constant h = [ M L2 T-1 ]
SI unit of speed of light c = m s-1
Hence dimension of speed of light = [ L T-1 ]
SI unit of gravitational constant = N m2 kg-2 = kg m s-2 m2 kg-2 = kg-1 m3 s-2
Hence dimension of gravitational constant = [ M-1 L3 T-2 ]
Let us do dimensional analysis to eqn.(1)

By equating power of each dimesnion , we get the following equation
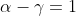 ............................... (2)
............................... (2)
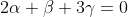 ........................(3)
........................(3)
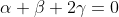 ..........................(4)
..........................(4)
By solving eqn.(2) , eqn.(3) and eqn.(4) , we get
α = 1/2 , β = 1/2 and γ = -1/2
Hence we can writte eqn.(1) as
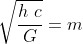
---------------------------------------------------------------------
If plancks constant h, speed of light c and universal gravitational constant G are combined to form the unit of length ,
then we have
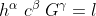 .................................(5)
.................................(5)
where l is length . 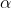 ,
, 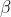 and
and 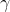 are constants to be determined by using dimensional analysis.
are constants to be determined by using dimensional analysis.
As it is done in previous case , if we do dimensional analysis for eqn.(5) , we get
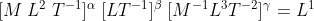
By equating power of each dimesnion , we get the following equation
α - γ = 0 ...................................(6)
2α + β + 3γ = 1 ........................(7)
α + β + 2 γ = 0 ......................(8)
By solving above equations, we get α = 1/2 , β = -3/2 and γ = 1/2
Hence eqn.(5) is written as

--------------------------------------------------------------------