NEET Class neet Answered

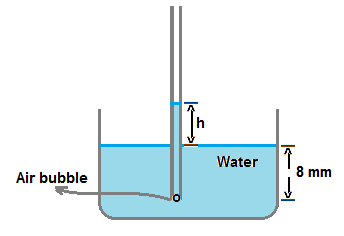
When the capillary tube of radius 2 mm is dipped inside water to a depth 8 mm , there is a capillary rise of water to a height h .

Height h of capillary rise is

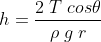
where T is surface tension of water , θ is angle of contact , ρ is density of water, g is acceleration due to gravity

and r is radius of capillary tube .

Angle θ of contact with water on glass is zero . Surface tension T of water  is 0.072 N/m .

Hence height h of capillary rise is

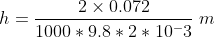
h = 7.3 × 10^-3 m = 7.3 mm

If the bubble is at the end of capillary tube inside water as shown in figure,

then pressure inside the bubble is  greater by (4T)/r than pressure outside bubble.

Pressure P inside the bubble is

P = P_a + [ ρ g (h+8) × 10^-3 ] + [ (4T)/r ]

where P_a is atmospheric pressure .

If P_g is gauge pressure inside the bubble , then

P_g = P - P_a = [ ρ × g × (h+8) × 10^-3 ] + [ (4T)/r ]

P_g = [ 1000 × 9.8 ×  (7.3 + 8.0 ) ] + [ ( 4 × 0.072 ) / 0.002 ]  \ Pa

P_g = 294  Pa