Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

integrate 2sinx-cosx+3/sinx-2cosx+1 dx
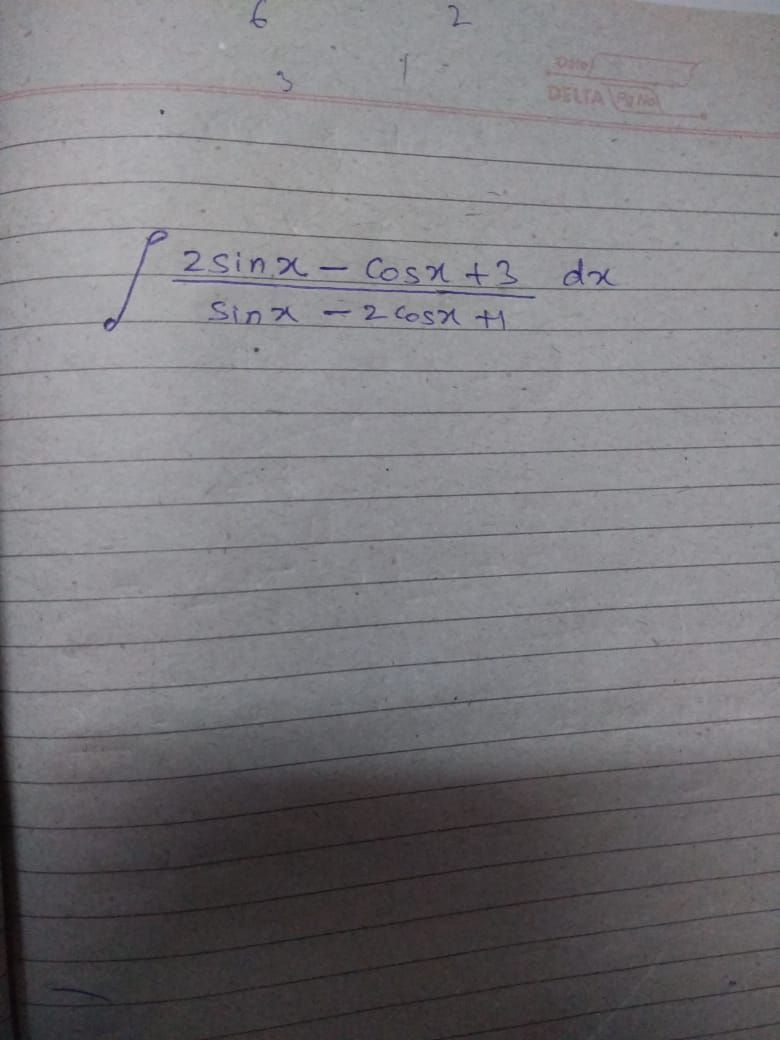
question image
Asked by ayush9828450465 | 15 Oct, 2020, 10:17: AM
answered-by-expert Expert Answer
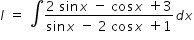
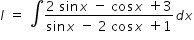
Given integration :- begin mathsize 14px style I space equals space integral fraction numerator 2 space sin x space minus space cos x space plus 3 over denominator sin x space minus space 2 space cos x space plus 1 end fraction d x end style
Let u = sinx - 2cosx +1 ,  then du = ( cosx+2sinx ) dx
 
numerator of integrand :-  (2 sinx - cosx +3 ) dx = ( 2sinx + cosx -2cosx +3 ) dx =  du + (3 - 2 cosx) dx
 
Hence given intgration becomes
 
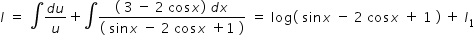begin mathsize 14px style I space equals space integral fraction numerator d u over denominator u end fraction plus integral fraction numerator left parenthesis space 3 space minus space 2 space cos x right parenthesis space d x over denominator left parenthesis space sin x space minus space 2 space cos x space plus 1 space right parenthesis end fraction space equals space log left parenthesis space sin x space minus space 2 space cos x space plus space 1 space right parenthesis space plus space I subscript 1 end style .....................(1)
Where 
 
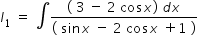begin mathsize 14px style I subscript 1 space equals space integral fraction numerator left parenthesis space 3 space minus space 2 space cos x right parenthesis space d x over denominator left parenthesis space sin x space minus space 2 space cos x space plus 1 space right parenthesis end fraction space end style......................(2)
To integrate above, we use the substitutions ,  t = tan(x/2) ,  sinx = 2t / ( 1+t2 ) , cosx = (1-t2 )/(1+t2 ) , dx = 2dt / ( 1+ t2 )
 
By using the above substitutions, we get
 
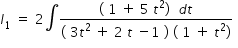begin mathsize 14px style I subscript 1 space equals space 2 integral fraction numerator left parenthesis space 1 space plus space 5 space t squared right parenthesis space space d t over denominator left parenthesis space 3 t squared space plus space 2 space t space minus 1 space right parenthesis space left parenthesis space 1 space plus space t squared right parenthesis end fraction space end style.........................(3)
Integrand in the above integration is written as partial fraction as given below
 
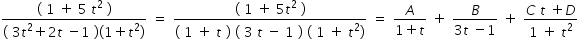begin mathsize 14px style fraction numerator left parenthesis space 1 space plus space 5 space t squared space right parenthesis over denominator left parenthesis space 3 t squared plus 2 t space minus 1 space right parenthesis left parenthesis 1 plus t squared right parenthesis end fraction space equals space fraction numerator left parenthesis space 1 space plus space 5 t squared space right parenthesis over denominator left parenthesis space 1 space plus space t space right parenthesis space left parenthesis space 3 space t space minus space 1 space right parenthesis space left parenthesis space 1 space plus space t squared right parenthesis end fraction space equals space fraction numerator A over denominator 1 plus t end fraction space plus space fraction numerator B over denominator 3 t space minus 1 end fraction space plus space fraction numerator C space t space plus D over denominator 1 space plus space t squared end fraction end style  ...................(4)
 
Hence we write
 
(1+5 t2 ) = A ( 3t -1 ) ( 1 + t2 ) + B ( 1+t) (1 +t2 ) + ( C t + D ) ( 1 + t ) ( 3 t -1 )  ........................(5)
 
if we put t = 1/3 in above eqn.(5) , we get B = 21/20
 
if we put t = -1 in above eqn.(5) , we get A = -3/4 
 
if we put t = 0 in above eqn.(5) , we get  1 = -A  +B -D  = (3/4) + 21/20 -D , hence D = 4/5
 
if we put t = 1 in above eqn.(5) , we get  6 = 4A  +4B  +( C+D)4  , By substituting values for A , B and D , we get C = 2/5
 
using the values A, B, C and D , we rewrite integration as given in eqn.(3) as
 
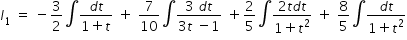
begin mathsize 14px style I subscript 1 space equals space minus 3 over 2 integral fraction numerator d t over denominator 1 plus t end fraction space plus space 7 over 10 integral fraction numerator 3 space d t over denominator 3 t space minus 1 end fraction space plus 2 over 5 integral fraction numerator 2 t d t over denominator 1 plus t squared end fraction space plus space 8 over 5 integral fraction numerator d t over denominator 1 plus t squared end fraction end style
Integration of each term in above equation is known . 
Hence after integration of each term , by using substitution t = tan(x/2) and after simplification , we get
 
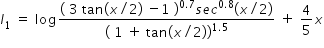
begin mathsize 14px style I subscript 1 space equals space log fraction numerator left parenthesis space 3 space tan left parenthesis x divided by 2 right parenthesis space minus 1 space right parenthesis to the power of 0.7 end exponent s e c to the power of 0.8 end exponent left parenthesis x divided by 2 right parenthesis over denominator left parenthesis space 1 space plus space tan left parenthesis x divided by 2 right parenthesis right parenthesis to the power of 1.5 end exponent end fraction space plus space 4 over 5 x end style
 
Hence using eqn.(1) , given integration becomes 
 
 
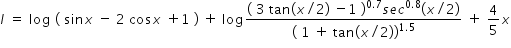
 begin mathsize 14px style I space equals space log space left parenthesis space sin x space minus space 2 space cos x space plus 1 space right parenthesis space plus space log fraction numerator left parenthesis space 3 space tan left parenthesis x divided by 2 right parenthesis space minus 1 space right parenthesis to the power of 0.7 end exponent s e c to the power of 0.8 end exponent left parenthesis x divided by 2 right parenthesis over denominator left parenthesis space 1 space plus space tan left parenthesis x divided by 2 right parenthesis right parenthesis to the power of 1.5 end exponent end fraction space plus space 4 over 5 x end style
 
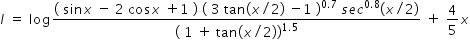
begin mathsize 14px style I space equals space log fraction numerator left parenthesis space sin x space minus space 2 space cos x space plus 1 space right parenthesis space left parenthesis space 3 space tan left parenthesis x divided by 2 right parenthesis space minus 1 space right parenthesis to the power of 0.7 end exponent space s e c to the power of 0.8 end exponent left parenthesis x divided by 2 right parenthesis over denominator left parenthesis space 1 space plus space tan left parenthesis x divided by 2 right parenthesis right parenthesis to the power of 1.5 end exponent end fraction space plus space 4 over 5 x end style
 
Answered by Thiyagarajan K | 15 Oct, 2020, 16:00: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Maths
in how many ways a team of 2 boys and 4 girls selected from 5 boys and 6 girls
Asked by pallavibirangal87 | 08 Dec, 2024, 10:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
if a chord of length 18 cm is 12 cm away from the centre then find the distance of 24 cm long chord from the centre
Asked by pritisindra6 | 06 Dec, 2024, 21:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
The number of ways in which at least one coin can be selected from 3 coins of one rupee, 4 coins of fifty paise, 5 coins of twenty paise and 6 coins of ten paise is-
Asked by kanishthkumawat | 29 Nov, 2024, 00:23: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
what is range of tan^-1 x
Asked by pawandhayal125 | 06 Oct, 2024, 10:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
what is 2+2
Asked by srishtipra2008 | 28 Sep, 2024, 10:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
n arithmetic means are inserted between the numbers 7 and 49. if the sum of these means is 364 then the sum of their squares is
Asked by yogeshsoni575 | 23 Sep, 2024, 23:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
consider a dodecagon then number of ways of selecting two triangles which can be made using the vertices of dodecagon so that they do not have a common side.
Asked by sumit.parsudih | 17 Sep, 2024, 22:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
the sum of infinite series 1/2(1/3+1/4)-1/4(1/3^2+1/4^2)+1/6(1/3^3+1/4^3)+
Asked by pritamlovevanshi5 | 15 Sep, 2024, 08:24: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
solve the equation 6x-y+3z=10 , 3x+6y=18 , x+y+5z=-10 by jacobis method with (3,0,-2) as the initial approcimate to the solution
Asked by ganeshbabugottapu7 | 12 Sep, 2024, 18:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
find the inverse of a Matrix by using gauss Jordan method -2. 1. 3 A = 0. -1. 1 1. 2. 0
Asked by ganeshbabugottapu7 | 10 Sep, 2024, 07:32: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt