CBSE Class 8 Answered
if the area of a rhombus is 48cm^2 , and one of its diagonal is 5 cm . find its altitude
Asked by ramaysah12 | 12 Mar, 2016, 06:38: PM
Given,
Area of Rhombus = 48 cm2
one diagonal = 5 cm
Area of a rhombus = 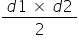 = altitude × side
= altitude × side
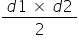 = altitude × side
= altitude × side 48 = 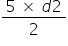
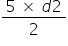
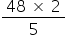 = d2
= d2length of diagonal 2 = 19.2 cm
We know, diagonals of a rhombus are perpendicular and bisect each other.
So, according to Pythagoras theorem,
side2 = 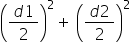
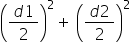
= 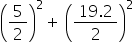
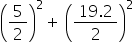
= (2.5)2 + (9.6)2
= 6.25 + 92.16
= 98.41
side = 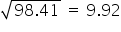
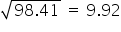
So, each side of the rhombus = 9.92 cm
altitude = area ÷ side
= 48 ÷ 9.92
= 4.83 cm
Hence, the height of the rhombus is 4.83 cm
Answered by Keravi Thanani | 05 Dec, 2017, 02:27: PM
Application Videos
Concept Videos
CBSE 8 - Maths
Asked by tejagshelar | 11 Feb, 2022, 08:52: PM
CBSE 8 - Maths
Asked by kritikarautela16.8cpsb | 29 Dec, 2021, 06:32: PM
CBSE 8 - Maths
Asked by pm6617978 | 28 Dec, 2021, 06:30: PM
CBSE 8 - Maths
Asked by shivanshipandey127 | 27 Dec, 2021, 03:45: PM
CBSE 8 - Maths
Asked by sejaldhaka | 05 Jan, 2021, 03:27: PM
CBSE 8 - Maths
Asked by Kiran | 31 Dec, 2019, 12:37: PM
CBSE 8 - Maths
Asked by rk97718824 | 09 Oct, 2019, 11:55: PM
CBSE 8 - Maths
Asked by Mohdayaz9921 | 04 Feb, 2019, 11:35: AM
CBSE 8 - Maths
Asked by Mohdayaz9921 | 28 Nov, 2018, 02:39: PM
CBSE 8 - Maths
Asked by Mohdayaz9921 | 27 Nov, 2018, 04:41: PM



