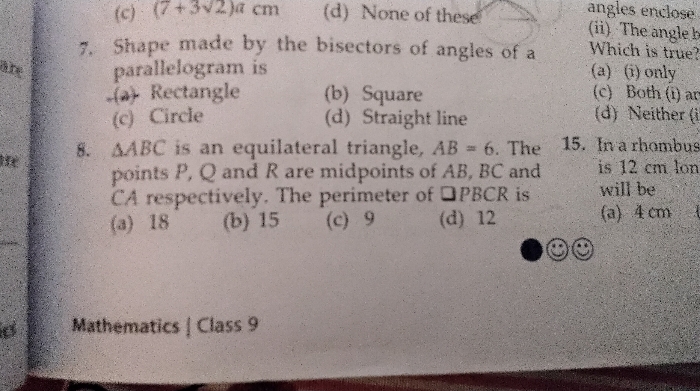Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

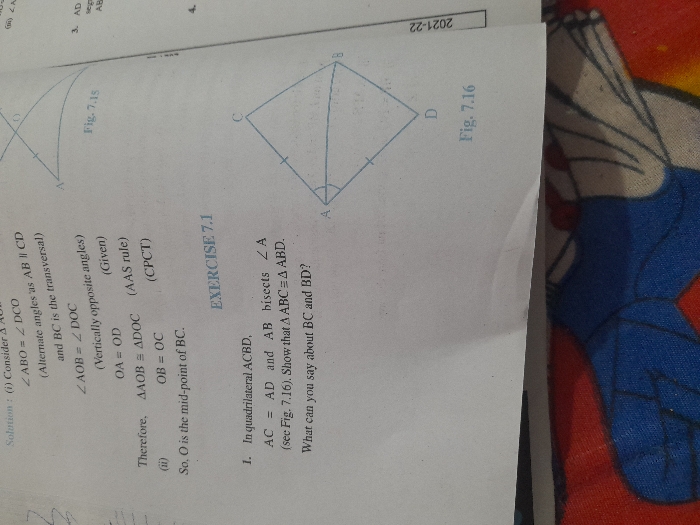
How will we prove that diameter is the longest chord of the circle
Asked by | 15 Jun, 2013, 06:14: PM
answered-by-expert Expert Answer
Take any chord in a circle, say with endpoints AB. Let O be the center of the circle. Then segments AO and BO are radii of the circle. AOB is a triangle, and we know that the sum of the lengths of two sides of a triangle is always greater than or equal to the length of the third side. So:

|AB| ? |AO| + |BO|
 
(Here |AB| means length of AB.)
 
So, the maximum length of the chord AB can be equal to |AO| + |BO|. Now AO and BO are the radii of the circle, hence |AO| + |BO| = 2r = d (diamter of the circle). 
 
So, maximum length of the chord AB = |AO| + |BO| = d
Hence diameter of the circle represents the longest chord in the circle.
Answered by | 15 Jun, 2013, 09:26: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
questions
question image
Asked by narendrapatidar39877 | 09 Mar, 2024, 11:01: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
mid point theorem
Asked by khshivam2006 | 26 Feb, 2024, 04:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
file
question image
Asked by maheshpatil2067 | 14 Jan, 2024, 04:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
solution
question image
Asked by harshitpal2115 | 30 Dec, 2023, 02:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
if ABCD is a llgm and X and Y are points on the diagonal BD such that DX=BY. Prove that a) AXCY is a llgm
Asked by borakartike2 | 29 Dec, 2023, 09:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
triangle ABC is an equilateral triangle, AB = 6cm. the points P,Q and R are midpoints of AB BC, CA respectively . the perimeter of □ PBCR is
question image
Asked by ghodage | 12 Dec, 2023, 07:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
the area of an equilateral triangle is 49√3 sq.cm, it's perimeter is
Asked by vijaykasaudhan913 | 10 Dec, 2023, 04:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
ABCD is quadrilateral in which P Q R S are mid points of the sides AB BC CD DA. AC is diagonal. show that SR is parallel to AC and SR= 1half 2 AC
Asked by aksharapatni | 30 Nov, 2023, 01:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
in right angle triangle ABC angle B =90 degrees and tanC=1/2.if AC=6cm then then the lenght of side BC is
Asked by rajetigirija | 19 Nov, 2023, 08:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
M is a point inside a square ABCD. AMCD is equilateral triangle and MC cuts diagonal DB at E. Then, ZBEC=..... (1) 75° (3) 105° (2) 90° (4) 60°
Asked by Krishna962511 | 23 Jan, 2023, 10:41: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×