CBSE Class 10 Answered
How to prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle
Asked by ssai6651 | 08 Jan, 2020, 07:39: AM
Your query is covered here. Refer to the solution of Q. 34. This is a very important Q for CBSE class 10 exam.
Answered by | 08 Jan, 2020, 13:26: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by Vidushi412 | 11 Aug, 2020, 22:20: PM
CBSE 10 - Maths
Asked by ssai6651 | 08 Jan, 2020, 07:39: AM
CBSE 10 - Maths
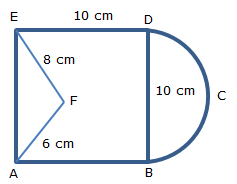
Asked by tejutanu2004 | 16 Sep, 2019, 20:27: PM
CBSE 10 - Maths
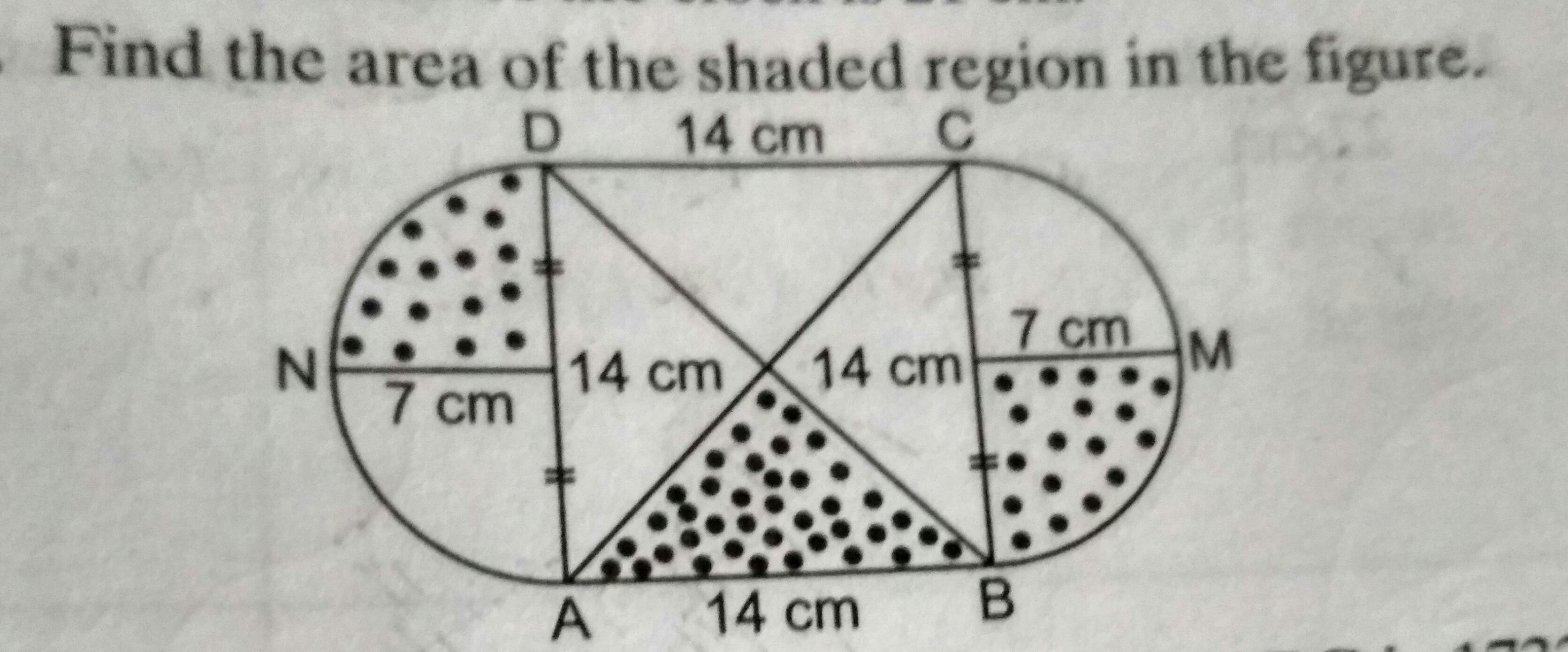
Asked by shailesh.solanki | 18 Mar, 2018, 19:29: PM
CBSE 10 - Maths
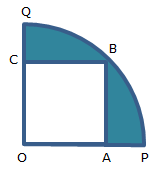
Asked by Topperlearning User | 27 Jul, 2017, 14:33: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 14:33: PM
CBSE 10 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 14:33: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 14:28: PM
CBSE 10 - Maths
Asked by Topperlearning User | 27 Jul, 2017, 14:33: PM









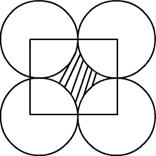
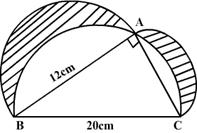
.jpg)