CBSE Class 9 Answered
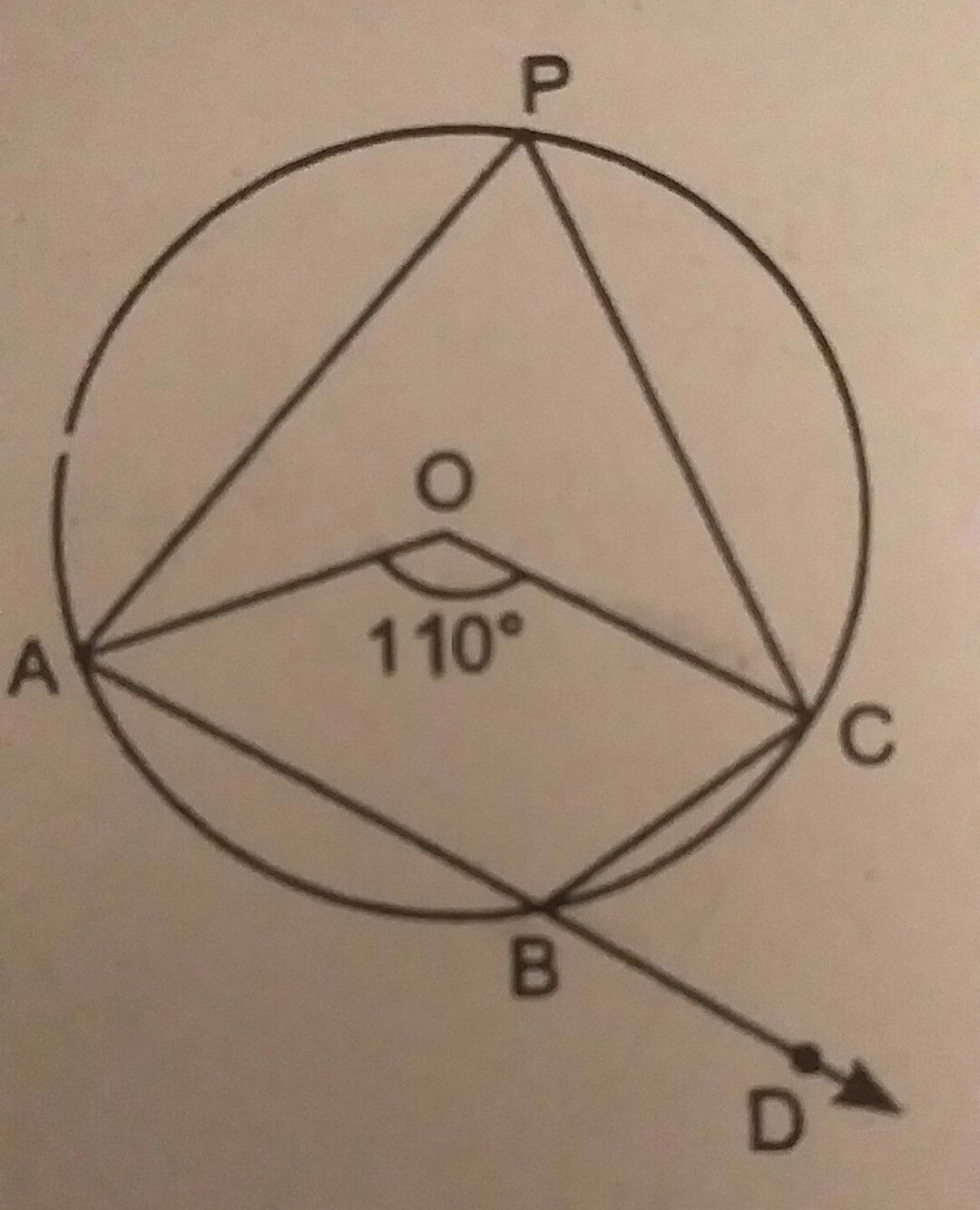
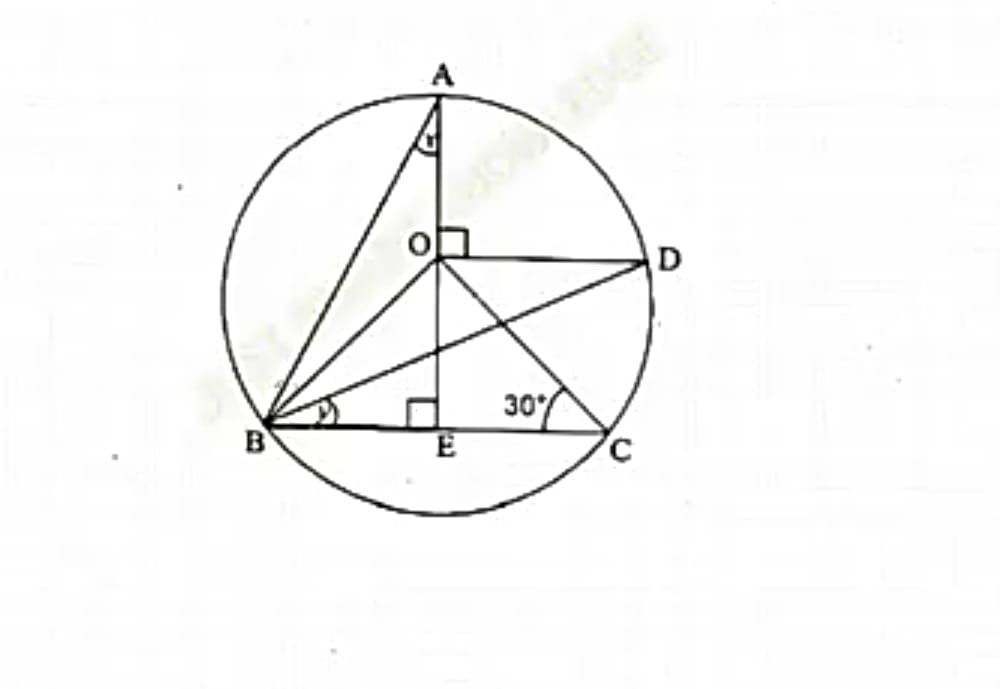
How to prove that angle subtended by the chord are equal to the chords?
Asked by Preeti | 11 Mar, 2017, 07:38: PM

I have proved it this way.
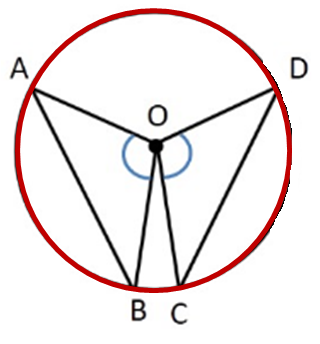

Now, since the framing of your question is weird. I should tell you that the theorem can also be
If the chords are equal of a circle, then the angle subtended by them are also equal.
In that case you can use the same figure and prove the triangles congruent by the SSS congruence criterion, and then prove the angles equal by cpct.
Answered by Rebecca Fernandes | 11 Mar, 2017, 08:03: PM
Concept Videos
CBSE 9 - Maths
Asked by geetaradha8835 | 16 Dec, 2022, 07:59: PM
CBSE 9 - Maths
Asked by sangeetabharti123456789 | 22 Feb, 2022, 09:01: AM
CBSE 9 - Maths
Asked by Samidhaindulkar133 | 11 Mar, 2021, 04:03: PM
CBSE 9 - Maths
Asked by harjot.arshleen | 03 Feb, 2021, 02:42: PM
CBSE 9 - Maths
Asked by lata15121995joshi | 03 Jan, 2020, 07:59: AM
CBSE 9 - Maths
Asked by Anubhavjain599 | 26 Nov, 2019, 05:53: PM
CBSE 9 - Maths
Asked by yogeshthakur3300 | 28 Dec, 2018, 08:24: AM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
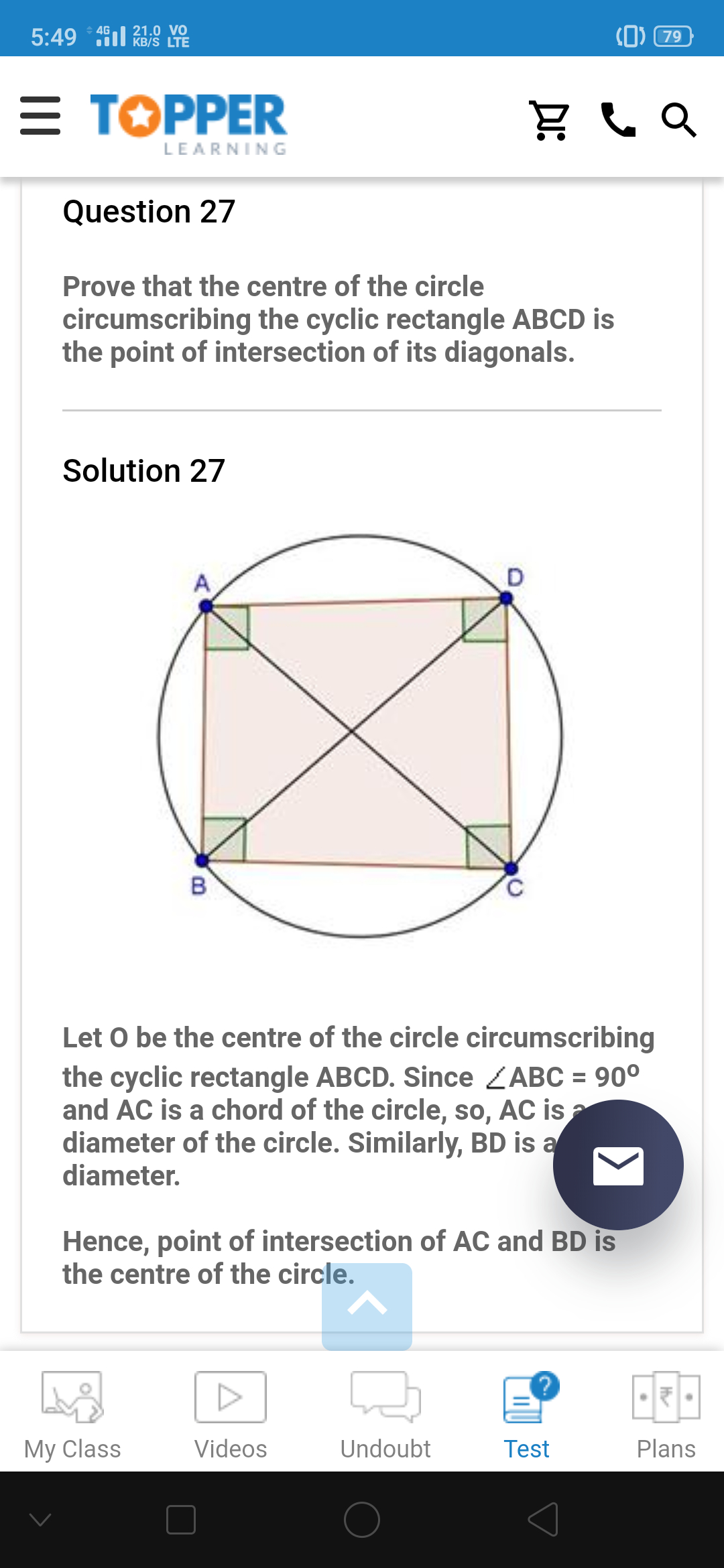
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM