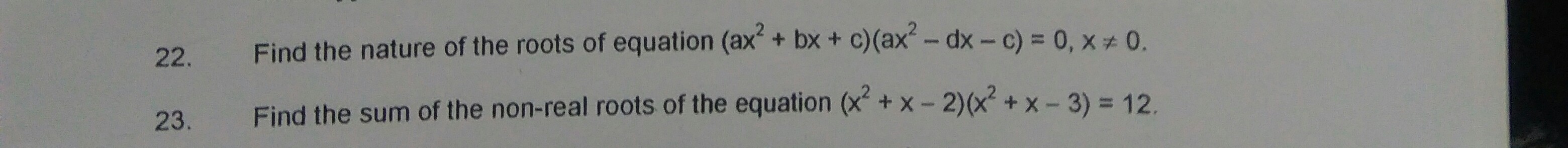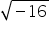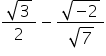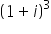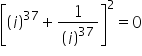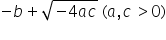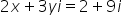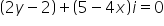CBSE Class 11-science Answered
For complex numbers according to the closure law of multiplication the product two of complex numbers is a complex number. but when we multiple the following two complex numbers...
x=(i+i)
y=(1-i)
x*y=i-(i sguared)=1-(-1)=1+1=2
which is a real number.
thus this proves the closure law to be incorrect. please explain.
Asked by Rida Mukadam | 05 Jun, 2015, 06:52: PM
Expert Answer
Every real number is a complex number with imaginary part as '0'.
The number '2' can be written as '2 + 0i'
The set of real numbers is a subset of set of complex numbers. Hence, the closure law of multiplication is still valid even if the result is a real number.
Answered by satyajit samal | 06 Jun, 2015, 08:56: PM
Concept Videos
-
Introduction to Complex Numbers
This video gives the introduction to Complex Numbers. -
Introduction to Complex Numbers
This video covers the introduction to Complex Numbers and some examples on ... -
Complex Numbers
This video covers the definition of complex number, iota, binary operation ...
CBSE 11-science - Maths
Asked by Ankitagarabadu1 | 20 Mar, 2018, 12:06: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 13 Sep, 2016, 03:24: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 08 Aug, 2014, 10:27: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 08 Aug, 2014, 10:36: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 08 Aug, 2014, 10:54: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 08 Aug, 2014, 10:41: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 08 Aug, 2014, 10:57: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 08 Aug, 2014, 10:58: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 08 Aug, 2014, 10:47: AM
ANSWERED BY EXPERT
