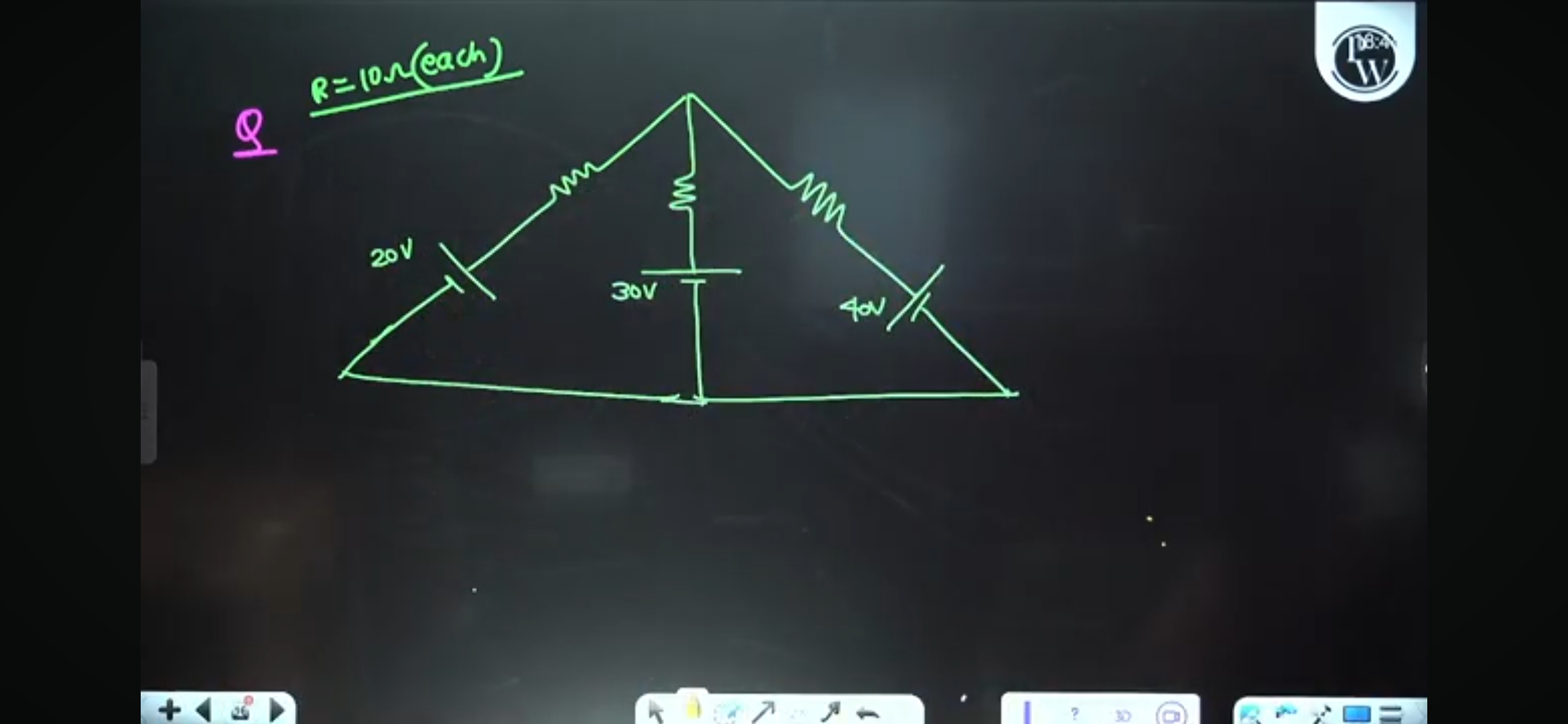
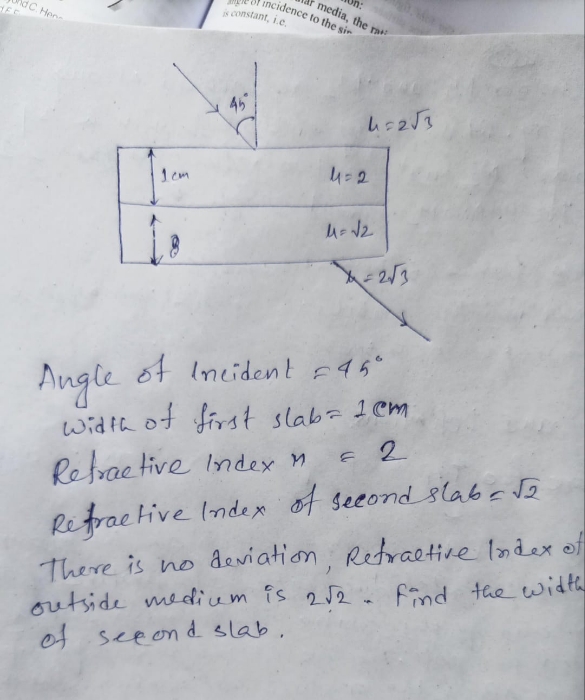
CBSE Class 12-science Answered
Derive mirror formula for concave mirror and state mirror formula.
Asked by polyrelation | 14 Mar, 2019, 21:17: PM
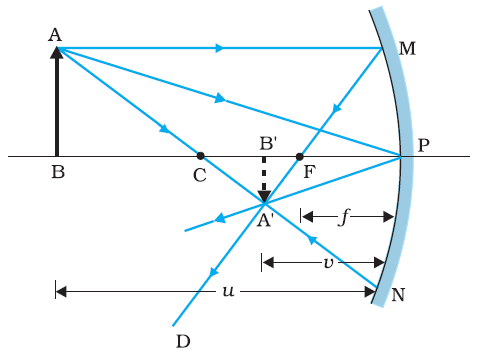
Figure shows the ray diagram considering three rays. It shows the image A′B′ (in this case, real) of an object AB formed by a concave
mirror. Thus, point A′ is image point of A if every ray originating at point A and falling on the concave mirror after reflection passes
mirror. Thus, point A′ is image point of A if every ray originating at point A and falling on the concave mirror after reflection passes
through the point A′.
We now derive the mirror equation or the relation between the object distance (u), image distance (v) and the focal length ( f ).
From Figure, the two right-angled triangles A′B′F and MPF are similar. (For paraxial rays, MP can be considered to be a straight line
perpendicular to CP.) Therefore,
From Figure, the two right-angled triangles A′B′F and MPF are similar. (For paraxial rays, MP can be considered to be a straight line
perpendicular to CP.) Therefore,
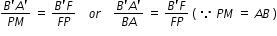 ......................................(1)
......................................(1)since 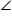 APB =
APB = 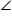 A'PB' , the right angled triangles A′B′P and ABP are also similar. Therefore,
A'PB' , the right angled triangles A′B′P and ABP are also similar. Therefore,
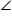 APB =
APB = 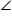 A'PB' , the right angled triangles A′B′P and ABP are also similar. Therefore,
A'PB' , the right angled triangles A′B′P and ABP are also similar. Therefore,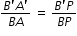 ...........................................(2)
...........................................(2)Comparing eqns.(1) and (2), we get
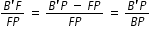 .........................................(3)
.........................................(3)Equation (3) is a relation involving magnitude of distances. We now apply the sign convention. We note that light travels from the object to
the mirror MPN. Hence this is taken as the positive direction.
the mirror MPN. Hence this is taken as the positive direction.
To reach the object AB, image A′B′ as well as the focus F from the pole P, we have to travel opposite to the direction of incident light.
Hence, all the three will have negative signs. Thus,
B'P = -v, FP = -f , BP = -u
using these convention in eqn.(3), we get
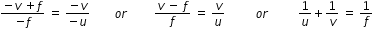 .............................(4)
.............................(4)Eqn.(4) is known as mirror formula
Answered by Thiyagarajan K | 14 Mar, 2019, 23:07: PM
Concept Videos
CBSE 12-science - Physics
Asked by jothisugashini216 | 16 Jul, 2024, 20:30: PM
CBSE 12-science - Physics
Asked by prithviraj.chopra2011 | 14 Jul, 2024, 23:00: PM
CBSE 12-science - Physics
Asked by basithhhabduuu | 14 Jul, 2024, 17:07: PM
CBSE 12-science - Physics
Asked by asmaabid356 | 10 Jul, 2024, 21:03: PM
CBSE 12-science - Physics
Asked by pushpamagadum21 | 09 Jul, 2024, 20:43: PM
CBSE 12-science - Physics
Asked by sumitghorband09 | 20 Jun, 2024, 21:42: PM
CBSE 12-science - Physics
Asked by axonuploadserver4 | 14 Jun, 2024, 17:41: PM
CBSE 12-science - Physics
Asked by trishaktiprasadmallik693 | 11 Jun, 2024, 07:17: AM
CBSE 12-science - Physics
Asked by rahuldevgayen4 | 10 Jun, 2024, 14:58: PM