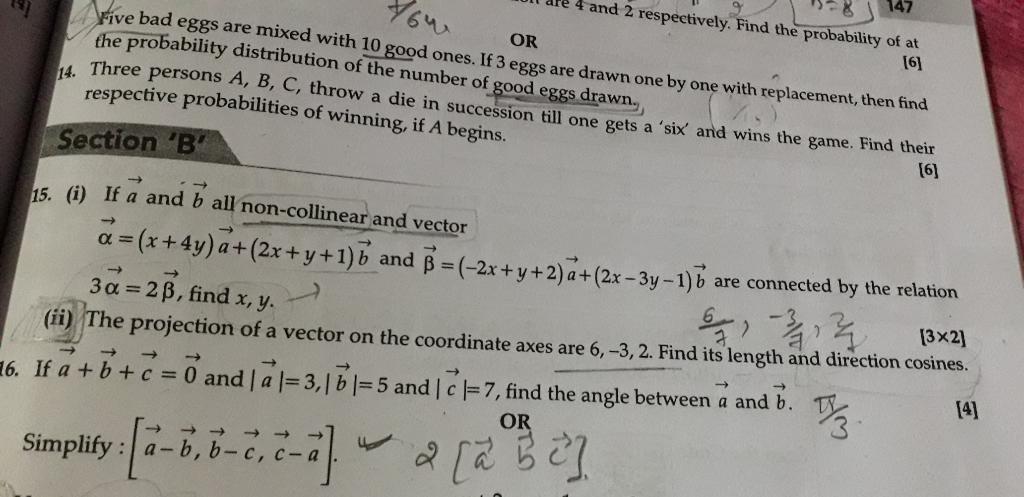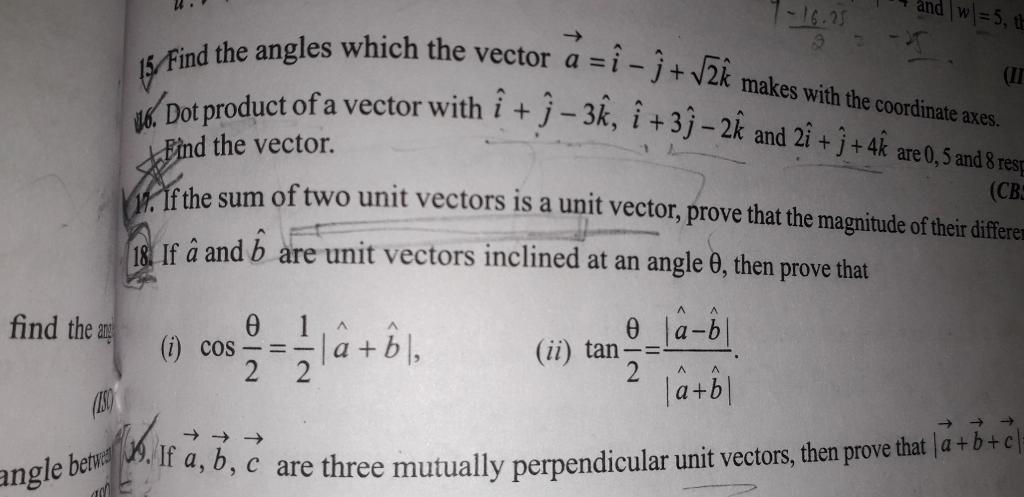CBSE Class 12-science Answered
Binomial Theorem
Asked by | 26 Jun, 2008, 06:11: PM
if we expand (1+x)n , then nC2 represents the coefficient of x2
also nCr can be written as nCn-r .
so (100C98)+(99C97)+.........+(3C1)+(2C0) = (100C2)+(99C2)+..............+(3C2)+(2C2)
so this expression will be equal to coeficient of x2 in (1+x)100 +(1+x)99+..............+(1+x)3+(1+x)2
sum of this series is (1+x)2( (1+x)99-1) / ( (1+x)-1 ) = (1/x) (1+x)2( (1+x)99-1 ) = (1/x) ( (1+x)101- (1+x)2 )
so we have to find coefficient of x3 in ( (1+x)101- (1+x)2 ) . since cofficient of x3 is zero in (1+x)2
so cofficient of x2 in this expression is 101C3
Answered by | 13 Sep, 2008, 07:38: PM
Concept Videos
CBSE 12-science - Maths
Asked by sdmbotch1123 | 18 Jan, 2023, 11:01: PM
CBSE 12-science - Maths
If |𝑎⃗| = 3 and −1 ≤ 𝑘 ≤ 2, then |𝑘𝑎⃗| lies in the interval
(a) [0,6] (b) [−3,6] (c) [3,6] (d) [1,2]


Asked by mohdtayyab682 | 18 Jan, 2023, 10:34: PM
CBSE 12-science - Maths
Asked by durgaprasaddurgaprasad174 | 01 Jul, 2022, 05:05: PM
CBSE 12-science - Maths
Asked by sujaychandramouli | 24 May, 2022, 10:46: AM
CBSE 12-science - Maths
Asked by abhimeena1011 | 18 Jan, 2022, 10:43: AM
CBSE 12-science - Maths
Asked by gurupadam3101985 | 11 Apr, 2020, 10:06: AM
CBSE 12-science - Maths
Asked by lovemaan5500 | 07 Feb, 2020, 09:49: AM
CBSE 12-science - Maths
Asked by lovemaan5500 | 07 Feb, 2020, 09:49: AM
CBSE 12-science - Maths
Asked by lovemaan5500 | 16 Dec, 2019, 09:34: PM
CBSE 12-science - Maths
Asked by Vivek.d8765 | 29 Oct, 2019, 10:14: PM