CBSE Class 9 Answered
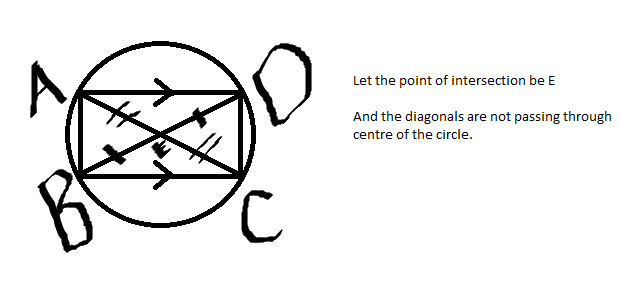
ABCD is a parallelogram. E and F are the mid points of the sides AB and CD respectively. Prove that the segments CE and AF trisect the diagonal BD.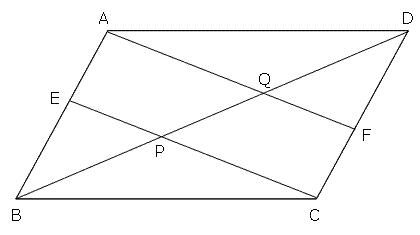 
Asked by Topperlearning User | 16 Aug, 2017, 03:10: PM
Expert Answer
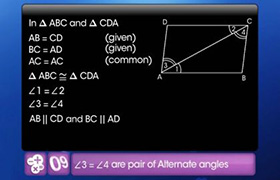
AE||CF and AE = CF (halves of opposite sides of a parallelogram)
Therefore, AECF is a parallelogram.
So, EC||AF
In 
DPC, FQ||CP and F is the mid point of DC
DPC, FQ||CP and F is the mid point of DCSo, PQ = QD
(Line through the mid point of one side of triangle and parallel to the another side, bisects the third side)
Similarly in ABQ, BP = PQ
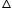ABQ, BP = PQHence, BP = PQ = QD
Thus, CE and AF trisect the diagonal BD.
Answered by | 16 Aug, 2017, 05:10: PM
CBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by vidyakashid7578 | 20 Sep, 2020, 01:36: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by dvmathur | 22 Nov, 2019, 02:42: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by prakash.sanyasi | 31 Oct, 2019, 11:27: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by prakash.sanyasi | 21 Oct, 2019, 04:03: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Topperlearning User | 16 Aug, 2017, 03:08: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Topperlearning User | 16 Aug, 2017, 03:09: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Topperlearning User | 16 Aug, 2017, 03:09: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Topperlearning User | 16 Aug, 2017, 03:10: PM
ANSWERED BY EXPERT