CBSE Class 9 Answered
ABC is an isosceles triangle with AB = AC. Bisectors of 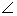 B and
B and  C intersect at O. Prove that BO = CO and AO bisects
C intersect at O. Prove that BO = CO and AO bisects  BAC.
BAC.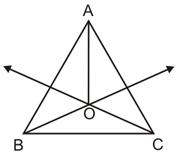

Asked by Topperlearning User | 10 Aug, 2017, 12:46: PM
In  ABC, AB = AC
ABC, AB = AC 
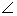 ABC =
ABC =  ACB
ACB
In  AOB and
AOB and  AOC
AOC
AO = AO
AB = AC
BO = OC
Answered by | 10 Aug, 2017, 14:46: PM
Concept Videos
CBSE 9 - Maths
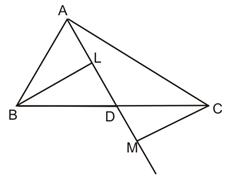
Asked by arahant2008 | 07 Oct, 2021, 21:38: PM
CBSE 9 - Maths
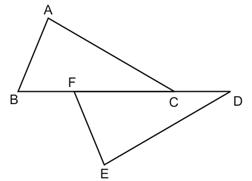
Asked by sharan192006 | 10 Sep, 2020, 15:27: PM
CBSE 9 - Maths
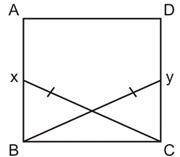
Asked by Nimmi | 26 Jan, 2019, 17:10: PM
CBSE 9 - Maths
Asked by Topperlearning User | 10 Aug, 2017, 12:35: PM
CBSE 9 - Maths
Asked by Topperlearning User | 10 Aug, 2017, 12:46: PM
CBSE 9 - Maths
Asked by Topperlearning User | 10 Aug, 2017, 12:44: PM
CBSE 9 - Maths
Asked by Topperlearning User | 10 Aug, 2017, 12:46: PM
CBSE 9 - Maths
Asked by Topperlearning User | 10 Aug, 2017, 12:36: PM