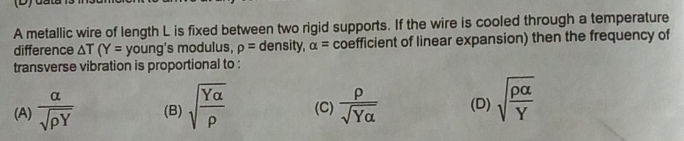JEE Class main Answered
A wave traveling from the left encounters a junction between the heavy string in which it moves and a lighter one. The incoming wave divides equally into a transmitted and reflected component. What is the ratio of densities of the string?
Asked by anaghaagarwal15 | 15 Mar, 2022, 17:15: PM
Amplitudes of reflected waves and transmitted waves are given as
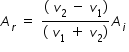 ............................(1)
............................(1) ..........................(2)
..........................(2)Where A denotes Amplitude of waves , subscript i denotes incident wave,
subscript r denotes reflected wave and subscript t denotes transmitted wave.
v1 and v2 are velocities in string-1 and string-2 respectively.
If the incoming wave is divided equally into reflected and transmitted component means
intensities of reflected and transmitted components are equal.
Since intensity of wave is proportional square of amplitude , we get
Ar2 = At2
Using eqn.(1) and (2) in above expression , we get after simplification as
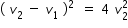
we get the following quadratic equation in v1 from above expression
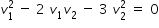
we get v2 = 3 v1 as acceptable solution from above expression
velocity of wave in the string is given as
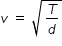
where T is tension in the string and d is linear mass density ( mass per unit length )
hence , v2  ( 1 / d)
( 1 / d)
 ( 1 / d)
( 1 / d)
Answered by Thiyagarajan K | 15 Mar, 2022, 23:07: PM
JEE main - Physics
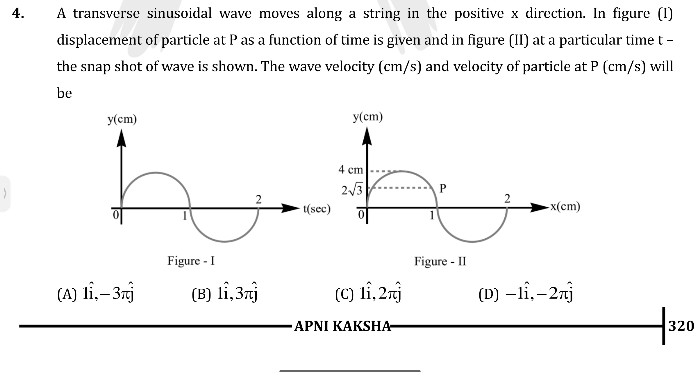
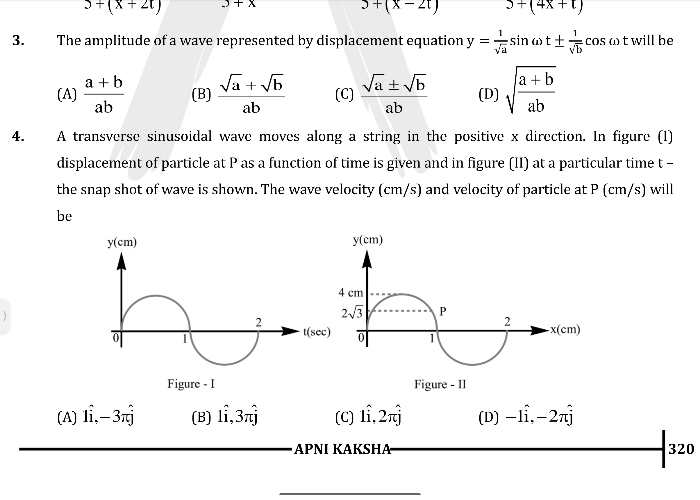
Asked by mahamahalakshmi6630 | 24 Jun, 2024, 20:42: PM
JEE main - Physics
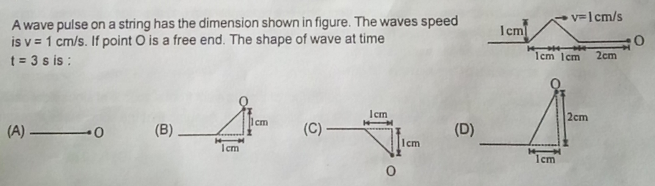
Asked by scnp978 | 15 Jun, 2024, 05:24: AM
JEE main - Physics
Asked by btennyson663 | 13 Jun, 2024, 20:02: PM
JEE main - Physics
Asked by piyurawriya | 20 Feb, 2024, 13:03: PM
JEE main - Physics
Asked by piyurawriya | 19 Feb, 2024, 23:19: PM
JEE main - Physics
Asked by siddhi.sristy | 21 Dec, 2023, 15:19: PM
JEE main - Physics
Asked by anaghaagarwal15 | 15 Mar, 2022, 17:15: PM
JEE main - Physics
Asked by sarveshvibrantacademy | 09 Apr, 2019, 19:25: PM
JEE main - Physics
Asked by sarveshvibrantacademy | 27 Mar, 2019, 10:28: AM
JEE main - Physics
Asked by sarveshvibrantacademy | 26 Mar, 2019, 11:24: AM