CBSE Class 9 Answered
A person being chased by a lion is running on a straight line towards his car
at a constant speed of 4m/s. The car is at a distance of d meters away from
the person. The lion is 26 m behind the person and running at a constant
speed of 6 m/s. The person reaches the car safely. What is the maximum
possible value of d?
Asked by Atal Kumar | 16 May, 2015, 04:02: AM
In order for the lion to catch the person over the distance d, the lion must reach the car at the same time as that of the person.
In the time t taken by the man to reach the car, the lion must travel a total distance of d + 26 m.
For the person:

For the lion:
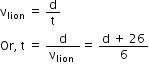
Since the man and the lion runs for the same time, we have
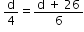
6d = 4d + 104
d = 52 m
Thus, the maximum possible distance distance is 52 m.
Answered by Yashvanti Jain | 13 Dec, 2017, 06:34: PM
Application Videos
Concept Videos
CBSE 9 - Physics
Asked by mailtoparvathyprajith | 06 Feb, 2024, 09:50: PM
CBSE 9 - Physics
Asked by mailtoparvathyprajith | 06 Feb, 2024, 09:10: PM
CBSE 9 - Physics
Asked by Anushkamishra385123 | 14 May, 2023, 12:39: PM
CBSE 9 - Physics
Asked by asyadav1230 | 20 Dec, 2022, 07:17: AM
CBSE 9 - Physics
Asked by rajesh kumar | 21 Oct, 2022, 08:15: PM
CBSE 9 - Physics
Asked by manognabandla2004 | 08 Sep, 2022, 07:55: PM
CBSE 9 - Physics
Asked by ayushyadav70303 | 12 Jul, 2022, 07:32: AM
CBSE 9 - Physics
Asked by drnaimansari2222 | 11 Jun, 2022, 04:28: PM
CBSE 9 - Physics
Asked by suzanesharma307 | 30 May, 2022, 11:03: PM
CBSE 9 - Physics
Asked by syedmehdiali543 | 17 Apr, 2022, 04:01: PM