CBSE Class 12-science Answered
A ladder 17 metre long is leaning against the wall. The base of the ladder is pulled away from the
wall at a rate of 5m/s. When the base of the ladder is 8 metres from the wall,
i) How fast is the top of the ladder moving down the wall?
ii) At what rate, the area of the triangle formed by the ladder, wall, and the floor, is
changing ?
Asked by jeevasankar123456 | 17 Jul, 2020, 17:14: PM
The ladder, ground and wall form a right angled triangle with the ladder as the hypotenuse.
Let x = base length (foot of ladder to wall), let y=height (top of ladder to ground),
Then by Pythagoras, x2 + y2 = 172 ... (1)
The bottom of the ladder is being pulled, so these distances are changing with time.
Differentiating (1) with respect to time, using the chain rule, gives:
2x(dx/dt) + 2y(dy/dt) = 0 (2)
Rearranging (2), we get dy/dt = -x/y(dx/dt) (3)
From the question, x = 8 m, dx/dt = 5 m/s.
If x = 8 m, then from (1), y = 15 m
Putting these values into (3) we get dy/dt = -(8/15) x (5) = -8/3 m/s
Answered by Renu Varma | 20 Jul, 2020, 11:41: AM
Concept Videos
CBSE 12-science - Maths
Asked by nirbhaysingh16102004 | 12 Jun, 2024, 10:04: AM
CBSE 12-science - Maths
Asked by saisidh05 | 04 Jul, 2022, 15:04: PM
CBSE 12-science - Maths
Asked by jeevasankar123456 | 17 Jul, 2020, 17:14: PM
CBSE 12-science - Maths
Asked by haroonrashidgkp | 08 Sep, 2018, 16:22: PM
CBSE 12-science - Maths
Asked by haroonrashidgkp | 08 Sep, 2018, 16:18: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 05 Aug, 2014, 12:38: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 05 Aug, 2014, 12:45: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 05 Aug, 2014, 12:53: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 05 Aug, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 05 Aug, 2014, 13:35: PM

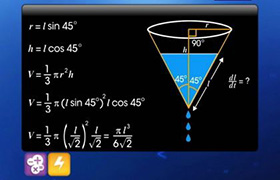




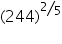 approximately using differentials.
approximately using differentials.