CBSE Class 12-science Answered
(a) If one of two identical slits producing interference in Young's experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern. (b) What king of fringes do you expect to observe if white light is used instead of monochromatic light?
MY DOUBT IS: In the first part of the question, shouldn't there be no interference pattern formed as introducing a glass sheet will make the slits non-coherent?
Asked by rayyan20151 | 19 Jan, 2020, 09:18: PM
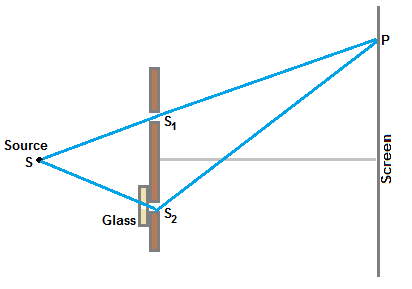
Figure shows the arrangement so that glass of thickness t is introduced before a slit S2 to reduce the intensity
of light from S2 as 50% of that of light from S1 .
To get constructive interference at P on screen , we need to find the path difference of two light beams
from source S by including the additional optical path introduced by glass.
Path difference Δd = [ SS1 + S1P + SS2 + (μ-1)t + S2P ]
where μ is the refractive index of glass and t is thickness of glass.
If Δd = nλ , then we get maximum intensity due to constructive interference , where n is integer and λ is wavelength.
Similarly if pathdifference satisfies destructive interference, we get minimum intensity at P.
Hence even after introduction of glass plate to reduce the intensity of light, we get interference pattern on screen
-----------------------------------------------------------------------------
Intensity I = I1 + I2 + 2 (I1I2)1/2 cosδ
where δ is phase difference
Let I1 = Io and I2 = ( Io / 2 )
For maximum, we have δ = 0 , Hence 

For minimum, we have δ = π , Hence 

Answered by Thiyagarajan K | 20 Jan, 2020, 08:41: AM
Concept Videos
CBSE 12-science - Physics
Asked by ankush76728 | 05 May, 2024, 09:55: PM
CBSE 12-science - Physics
Asked by heymindurownbusiness | 04 May, 2024, 11:15: AM
CBSE 12-science - Physics
Asked by talulu | 01 May, 2024, 05:14: PM
CBSE 12-science - Physics
Asked by kanishkg511 | 30 Apr, 2024, 07:25: PM
CBSE 12-science - Physics
Asked by sahoobanita89 | 30 Apr, 2024, 05:10: AM
CBSE 12-science - Physics
Asked by divakar.9124 | 27 Apr, 2024, 10:42: PM
CBSE 12-science - Physics
Asked by panneer1766 | 24 Apr, 2024, 01:52: PM
CBSE 12-science - Physics
Asked by artabandhusahu85 | 24 Apr, 2024, 12:07: PM
CBSE 12-science - Physics
Asked by niharvijayvargiya5 | 23 Apr, 2024, 06:40: PM