A car is moving at a constant speed of 40km/h along a straight road which heads towards a large vertical well and makes a sharp 90 degree turn by the wall .a fly flying at a constant speed of 100km/h, starts from the wall towards the car at an instant when the car is 20km away, flies until it reaches the glass pane of the car and returns to the wall at same speed. it continues to fly between the car and the wall till the car makes the 90 degree turn .

 

(a) what is the total distance the fly has travelled during this period?

(b) how many trips has it made between the car and the wall?

(a) First, calculate the time taken by the car to travel the distance of 20 km before the turn.Using the value of the time taken in the above case and also the speed of the car as 100 km/h, calculate the total distance covered.

(b) Suppose the car is at a distance say x km away from the wall at point A when the fly is at the wall (point O).

The fly hits the glass pane at point B, taking time t, then we have

AB − (40 km/hr)t and OB − (100 km/hr)t

→ x = AB + OB − (140 km/hr) t

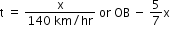
The fly now returns to the wall and during the time the car moves the distance BC.

The time taken by the fly in the return path is given as

 

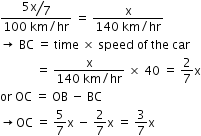
If at the start of the round trip the car is at a distance x away than it is [93/70x] away when the next trip again begins.

Distance of the car at the start of the 1^st trip = 20 km

→ Distance of the car at the start of the 2^nd trip = (3/7) × 20 km

→ Distance of the car at the start of the 3^rd trip = (3/7)² × 20 km

→ Distance of the car at the start of the n^th trip = (3/7)^n-1 × 20 km

Trips will continue till the car reaches the turn where the distance reduces to zero.

This will be the case when n becomes infinity.

Thus, the fly makes an infinite number of trips before the turn.