Class 10 SELINA Solutions Maths Chapter 19 - Constructions (Circles)
Constructions (Circles) Exercise Ex. 19
Solution 2
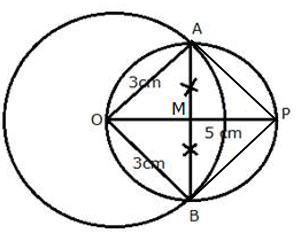
Steps Of Construction:
i) Draw a circle with centre O and radius 3 cm.
ii) From O, take a point P such that OP = 5 cm
iii) Draw a bisector of OP which intersects OP at M.
iv) With centre M, and radius OM, draw a circle which intersects the given circle at A and B.
v) Join AP and BP.
AP and BP are the required tangents.
On measuring AP = BP = 4 cm
Solution 2
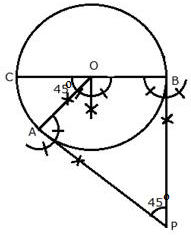
Steps of Construction:
i) Draw a circle with centre O and radius 5 cm
ii) Draw arcs making an angle of 180º - 45º = 135º at O such that ![]() AOB = 135º
AOB = 135º
iii) AT A and B, draw two rays making an angle of 90º at each point which meet each other at point P, outside the circle.
Thus, AP and BP are the required tangents which make an angle of 45º with each other at P.
Solution 4
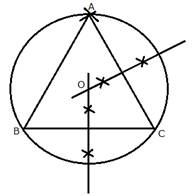
Steps of construction:
i) Draw a line segment BC = 4.5 cm
ii) With centers B and C, draw two arcs of radius 4.5 cm which intersect each other at A.
iii) Join AC and AB.
iv) Draw perpendicular bisectors of AC and BC intersecting each other at O.
v) With centre O, and radius OA or OB or OC draw a circle which will pass through A, B and C.
This is the required circumcircle of triangle ABC.
On measuring the radius OA = 2.6 cm
Solution 5
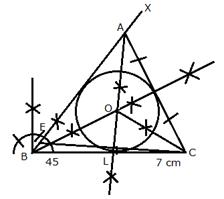
Steps of Construction:
i) Construction of triangle:
a) Draw a line segment BC = 7 cm
b) At B, draw a ray BX making an angle of 45oand cut off BE = AB - AC = 1 cm
c) Join EC and draw the perpendicular bisector of EC intersecting BX at A.
d) Join AC.
![]() is the required triangle.
is the required triangle.
ii) Construction of incircle:
e) Draw angle bisectors of ![]() and
and ![]() intersecting each other at O.
intersecting each other at O.
f) From O, draw perpendiculars OL to BC.
g) O as centre and OL as radius draw circle which touches the sides of the ![]() . This is the required in-circle of
. This is the required in-circle of ![]() .
.
On measuring, radius OL = 1.8 cm
Solution 6
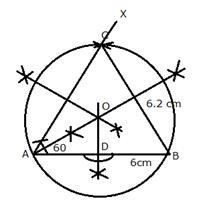
Steps of construction:
i) Draw a line segment AB = 6 cm
ii) At A, draw a ray making an angle of 60o with AB.
iii) With B as centre and radius = 6.2 cm, draw an arc which intersects ray AX at C.
iv) Join BC.
![]() is the required triangle.
is the required triangle.
v) Draw the perpendicular bisectors of AC and BC intersecting each other at O.
vi) With centre O, and radius as OA or OB or OC, draw a circle which will pass through A, B and C.
vii) From O, draw ![]() .
.
Proof: In right ![]() and
and ![]()
OA = OB (radii of same circle)
Side OD = OD (common)
![]()
Solution 7
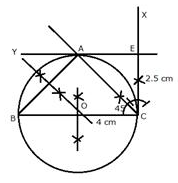
Steps of Construction:
i)Draw a line segment BC = 4 cm.
ii) At C, draw a perpendicular line CX and from it, cut off CE = 2.5 cm.
iii) From E, draw another perpendicular line EY.
iv) From C, draw a ray making an angle of 45o with CB, which intersects EY at A.
v) Join AB.
![]() is the required triangle.
is the required triangle.
vi) Draw perpendicular bisectors of sides AB and BC intersecting each other at O.
vii) With centre O, and radius OB, draw a circle which will pass through A, B and C.
Measuring the radius OB = OC = OA = 2 cm
Solution 8

i) Point O is called the circumcentre of circumcircle of ![]() .
.
ii) OA, OB and OC are the radii of the circumcircle. Hence, OA = OB = OC
iii) Yes, the perpendicular bisector of BC will pass through O.
Solution 9
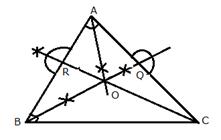
i) O is called the incentre of the incircle of ![]() .
.
ii) OR and OQ are the radii of the incircle and OR = OQ.
iii) OC is the bisector of angle C
![]()
Solution 10
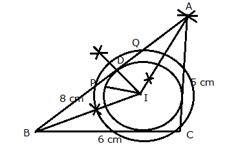
Steps of Construction:
i) Draw a line segment BC = 6 cm.
ii) With centre B and radius 8 cm draw an arc.
iii) With centre C and radius 5 cm draw another arc which intersects the first arc at A.
iv) Join AB and AC.
![]() is the required triangle.
is the required triangle.
v) Draw the angle bisectors of ![]() intersecting each other at I. Then I is the incentre of the triangle ABC
intersecting each other at I. Then I is the incentre of the triangle ABC
vi) Through I, draw ![]()
vii) Now from D, cut off ![]()
viii) With centre I, and radius IP or IQ, draw a circle which will intersect each side of triangle ABC cutting chords of 2 cm each.
Solution 11

Steps of Construction:
i) Draw a regular hexagon ABCDEF with each side equal to 5 cm and each interior angle 120º.
ii) Join its diagonals AD, BE and CF intersecting each other at O.
iii) With centre as O and radius OA, draw a circle which will pass through the vertices A, B, C, D, E and F.
This is the required circumcircle.
Solution 12
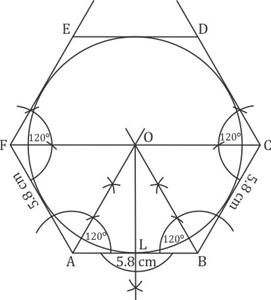
Steps of Construction:
i) Draw a line segment AB = 5.8 cm
ii) At A and B, draw rays making an angle of 120o each and cut off AF = BC = 5.8 cm
iii) Again at F and C, draw rays making an angle of 120o each and cut off FE = CD = 5.8 cm.
iv) Join DE. Then ABCDEF is the regular hexagon.
v) Draw the bisectors of ![]() intersecting each other at O.
intersecting each other at O.
vi) From O, draw ![]()
vii) With centre O and radius OL, draw a circle which touches the sides of the hexagon.
This is the required incircle of the hexagon.
Solution 13
i.
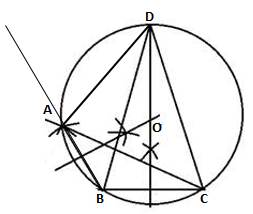
- Draw a line BC = 5.5 cm.
- Draw AB = 6 cm, such that m∠ABC = 120°.
- Construct the perpendicular bisectors of AB and BC, such that they intersect at O.
- Draw a circle with O as the radius.
ii.
(e) Extend the perpendicular bisector of BC, such that it intersects the circle at D.
(f) Join BD and CD.
(g) Here BD = DC and hence point D is equidistant from B and C.
(h) Join AD
Thus, ABCD is the reuired cyclic quadrilateral.
Solution 14

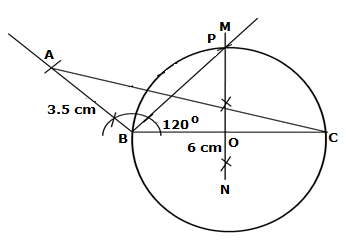
Solution 15
Steps for construction:
- Draw AB = 5 cm using a ruler.
- With A as the centre cut an arc of 3 cm on AB to obtain C.
- With A as the centre and radius 2.5 cm, draw an arc above AB.
- With same radius, and C as the centre draw an arc to cut the previous arc and mark the intersection as O.
- With O as the centre and radius 2.5 cm, draw a circle so that points A and C lie on the circle formed.
- Join OB.
- Draw the perpendicular bisector of OB to obtain the mid-point of OB, M.
- With the M as the centre and radius equal to OM, draw a circle to cut the previous circle at points P and Q.
- Join PB and QB. PB and QB are the required tangents to the given circle from exterior point B.
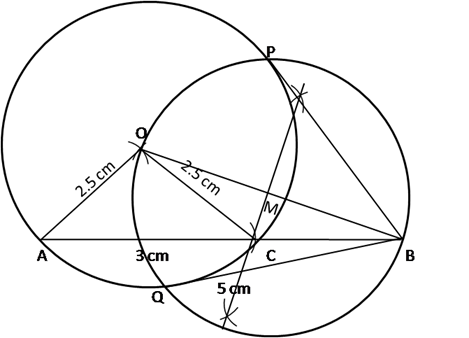
QB = PB = 3 cm
That is, length of each tangent is 3 cm.
Solution 16
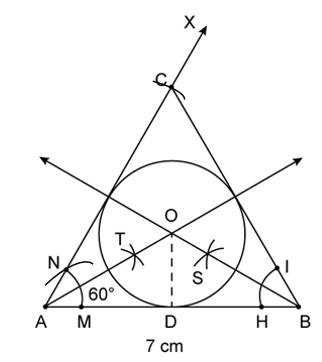
Steps of construction :
1. Draw a line AB = 7 cm.
2. Taking A as centre and any radius, draw an arc of a circle which intersects AB at M.
3. Taking M as centre and with the same radius as before drawn an arc intersecting previously drawn arc, at point N.
4. Draw the ray AX passing through N, then ![]()
5. Taking A as centre and radius equal to 5 cm, draw an arc cutting AX at C.
6. Join BC
7. The required triangle ABC is obtained.
8. Draw angle bisector of ∠CAB which is the locus of points equidistant from AB and AC.
9. Draw angle bisector of ∠ABC which is the locus of points equidistant from BA and BC.
10. Mark the intersection of angle bisectors as O.
11. Draw OD perpendicular to AB.
10. With O as center and radius OD, draw a circle which will touch all the three sides of triangle ABC.
Solution 17
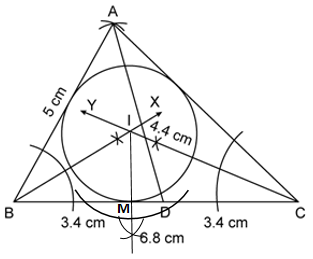
Steps for construction :
i. Draw BC = 6.8 cm.
ii. Mark point D where BD = DC = 3.4 cm, which is the mid-point of BC.
iii. Mark a point A which is intersection of arcs AD = 4.4 cm and AB = 5 cm from a point D and B respectively.
iv. Join AB, AD and AC.
ABC is the required triangle and AD is the median.
v. Draw bisectors of angle B and angle C which are ray BX and CY. Let these bisectors intersect at point I.
vi. Draw IM perpendicular to BC, where I is the incentre of a circle.
vi. Taking IM as radius, draw incircle of a triangle ABC.
Solution 18
Steps for construction :
i. Draw concentric circles of radius 4 cm and 6 cm with centre of O.
ii. Take any point P on the outer circle.
iii. Join OP.
iv. Draw perpendicular bisector of OP intersecting OP at point M. Then, M is the midpoint of OP.
v. Take length = OM, mark arcs from M on the inner circle as A and B respectively.
vi. Join PA and PB.
We observe that PA and PB are tangents from outer circle to inner circle are equal of a length 4.5 cm each.

Solution 19
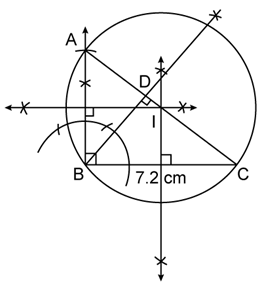
Steps for construction :
i. Draw BC = 7.2 cm.
ii. Draw an angle ABC = 90° using compass.
iii. From B, mark a point A at a distance of 6 cm from B.
iv. Join AC.
Thus, ABC is the required right-angled triangle.
v. From point B, draw perpendicular to AC using compass intersecting AC at point D.
v. Draw perpendicular bisectors of AB and BC which intersect at I, where I is the circumcentre of a circle.
vi. Draw circumcircle using circumcentre I. we get radius of a circle is 4.7 cm.
Solution 1(a)
Correct option: (iv) none of these
Point P is the intersection of angle bisector of ∠A and perpendicular bisector of side AB.
Hence, it is neither incentre nor circumcenter.
Also, PB does not bisect ∠B.
Solution 1(b)
Correct option: (ii) bisectors of its angles
Incentre of a triangle is the point of intersection of the bisector of its angles.
Solution 1(c)
Correct option: (ii) not equal
If a circle is inscribed in a regular hexagon, its radius and the length of the side of the regular hexagon are not equal
Solution 1(d)
Correct option: (i) equal
Whenever a circle circumscribes a given regular hexagon, its radius is always equal to the length of the side of the regular hexagon.
Solution 1(e)
Correct option: (iii) 45o
For octagon, number of sides = n = 8
Therefore, angle subtended by each side of regular octagon at the centre of the circle ![]()
Solution 1(f)
Correct option: (i) equal to radius of the circle
In ∆AOB, ∠AOB = 60o
OB = OA = radius of the circle
⇒ ∠OAB = ∠OBA = xo
Now, ∠AOB + ∠OAB + ∠OBA = 180o
⇒ 60o + x + x = 180o
⇒ 60o + 2x = 180o
⇒ x = 60o
Hence, ∆AOB is an equilateral triangle.
Therefore, AB = OA = OB = Radius of the circle
Solution 1(g)
Correct option: (i) 60o
For a regular six-sided polygon ABCDEF, n = 6
Therefore, ∠DOE ![]()
*Eight-sided polygon will have 8 vertices. Hence, ABCDEF cannot be eight-sided polygon.
Solution 1(h)
Correct option: (iii) 120o
Angle between two radii of a circle = 60o
Angle at the point of contact of tangent and radius of a circle = 90o
Therefore, the angle between corresponding tangents
= 360o – 90o – 90o – 60o
= 120o
Solution 1(i)
Correct option: (ii) ∠BCA
The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.
Therefore, ∠BAQ = ∠BCA
Solution 1(j)
Correct option: (iii) 90o

Angle in a semi-circle is a right angle.

