Class 10 SELINA Solutions Maths Chapter 2 - Banking (Recurring Deposit Accounts)
Banking (Recurring Deposit Accounts) Exercise Ex. 2
Solution 1(a)
Correct Option: (i) Rs. 270
P = Rs. 900, n = 8 and R = 10%
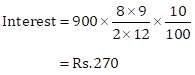
Solution 1(b)
Correct Option: (ii) Rs. 1800
I = Rs. 1404, n = 12 and R = 12%
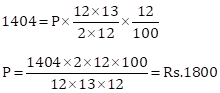
Solution 1(c)
Correct Option: (ii) Rs. 24000
P = Rs. 1000, n = 2 years = 24, R = 10%
Total sum deposited by Manish = Rs. 1000 × 24 = Rs. 24000
Solution 1(d)
Correct Option: (i) 20%
P = Rs. 800, n = one and half years = 18, I = Rs. 2280
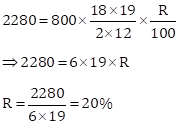
Note: Back answer is incorrect.
Solution 2
For A
Installment per month(P) = Rs 1,200
Number of months(n) = 3 × 12 = 36
Rate of interest(r)= 10% p.a.

The amount that A will get at the time of maturity
=Rs (1,200 x 36)+ Rs 6,660
=Rs 43,200+ Rs 6,660
= Rs 49,860
For B
Installment per month(P) = Rs 1,500
Number of months(n) = 2.5 × 12 = 30
Rate of interest(r)= 10% p.a.

The amount that B will get at the time of maturity
=Rs(1,500 x 30)+ Rs 5,812.50
=Rs 45,000+ Rs 5,812.50
= Rs 50,812.50
Difference between both amounts= Rs 50,812.50 - Rs 49,860
= Rs 952.50
Then B will get more money than A by Rs 952.50 Ans.
Solution 3
Let Installment per month(P) = Rs y
Number of months(n) = 12
Rate of interest(r)= 11%p.a.

Maturity value= Rs (y x 12) + Rs 0.715 y = Rs 12.715 y
Given maturity value= Rs 12,715
Then Rs 12.715 y = Rs 12,715
![]() Ans.
Ans.
Solution 4
Let Installment per month(P) = Rs y
Number of months(n) = 3.5 × 12 = 42
Rate of interest(r) = 12% p.a.

Maturity value= Rs(y x 42) + Rs 9.03y = Rs 51.03y
Given maturity value = Rs 10,206
Then Rs 51.03y = Rs 10206
![]() Ans.
Ans.
Solution 5
(a)
Installment per month(P) = Rs 140
Number of months(n) = 4 × 12 = 48
Let rate of interest(r)= r %p.a.

Maturity value= Rs (140 x 48) + Rs (137.20)r
Given maturity value= Rs 8,092
Then Rs(140 x 48)+Rs (137.20)r = Rs 8,092
![]() 137.20r = Rs 8,092 - Rs 6,720
137.20r = Rs 8,092 - Rs 6,720
![]() r =
r = ![]()
(b)
Installment per month(P) = Rs 300
Number of months(n) = 4 × 12 = 24
Let rate of interest(r)= r %p.a.

Maturity value= Rs (300 x 24)+Rs(75)r
Given maturity value = Rs 7,725
Then Rs(300 x 24) + Rs(75)r = Rs 7,725
![]() 75 r = Rs 7,725 - Rs 7,200
75 r = Rs 7,725 - Rs 7,200
![]() r =
r = ![]()
Solution 6
Installment per month(P) = Rs 150
Number of months(n) = 8
Rate of interest(r)= 8% p.a.

The amount that Manish will get at the time of maturity
=Rs (150 x 8)+ Rs 36
=Rs 1,200+ Rs 36
= Rs 1,236 Ans.
Solution 7
Installment per month(P) = Rs 1,200
Number of months(n) = n
Let rate of interest(r)= 8 %p.a.

Maturity value= Rs (1,200 x n) + Rs 4n (n + 1)= Rs (1200n + 4n2 + 4n)
Given maturity value= Rs 12,440
Then 1200n + 4n2 + 4n = 12,440
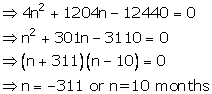
Then number of months = 10 Ans.
Solution 8
Installment per month(P) = Rs 300
Number of months(n) = n
Let rate of interest(r)= 12 %p.a.

Maturity value= Rs (300 x n) + Rs 1.5n(n + 1)
= Rs (300n + 1.5n2 + 1.5n)
Given maturity value = Rs 8,100
Then 300n + 1.5n2 + 1.5n = 8,100
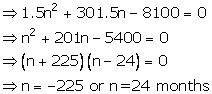
Then time = 2 years
Solution 9
(i)
Maturity value = Rs 67,500
Money deposited = Rs 2,500 x 24 = Rs 60,000
Then total interest earned = Rs 67,500 - Rs 60,000 = Rs 7,500 Ans.
(ii)
Installment per month(P) = Rs 2,500
Number of months(n) = 24
Let rate of interest(r)= r %p.a.

Then 625 r = 7500
![]()
Solution 10
Interest, I = Rs. 1,200
Time, n = 2 years = 2 × 12 = 24 months
Rate, r = 6%
(i) To find: Monthly installment, P
Now,

So, the monthly installment is Rs. 800.
(ii) Total sum deposited = P × n = Rs. 800 × 24 = Rs. 19,200
∴ Amount of maturity = Total sum deposited + Interest on it
= Rs. (19,200 + 1,200)
= Rs. 20,400
Banking (Recurring Deposit Accounts) Exercise TEST YOURSELF
Solution 1(a)
Correct Option: (ii) 9.6%
P = Rs. 500, n = 24,
Total sum deposited = Rs. 500 × 24 = Rs. 12000
![]()
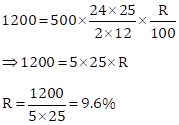
Solution 1(b)
Correct Option: (iv) Rs. 1087.50
P = Rs. 50, n = 20 and R = 10%
Total sum deposited = Rs. 50 × 20 = Rs. 1000
![]()
Maturity Value = Total sum deposited + Interest on it
= Rs. (1000 + 87.50)
= Rs. 1087.50
Solution 1(c)
Correct Option: (iii) Rs. 100
I = Rs. 36, n = 8 and R = 12%
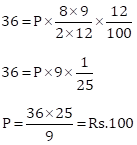
Solution 1(d)
Correct Option: (iv) Rs. 7,500
Total sum deposited = Rs. 5000 × 12 = Rs. 60,000
Maturity Value = Total sum deposited + Interest on it
Therefore, interest = Maturity Value – Total sum deposited
= Rs. 67,500 – Rs. 60,000
= Rs. 7,500
Solution 1(e)
Correct Option: (ii) 2%
Let sum = P
n = 15,
![]()
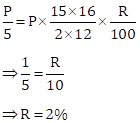
Solution 2
Installment per month(P) = Rs 600
Number of months(n) = 4 × 12 = 48
Rate of interest(r)= 8%p.a.
_21Maynewformat_files/20140521155159_image015.gif)
The amount that Manish will get at the time of maturity
=Rs (600 x 48)+ Rs 4,704
=Rs 28,800+ Rs 4,704
= Rs 33,504 Ans.
Solution 3
Installment per month(P) = Rs 80
Number of months(n) = 18
Let rate of interest(r)= r % p.a.
_21Maynewformat_files/20140521155159_image017.gif)
Maturity value= Rs (80 x 18) + Rs (11.4r)
Given maturity value= Rs 1,554
Then Rs (80 x 18)+Rs (11.4r) = Rs 1,554
![]() 11.4r = Rs 1,554 - Rs 1,440
11.4r = Rs 1,554 - Rs 1,440
![]()
Solution 4
Installment per month(P) = Rs 400
Number of months(n) = n
Let rate of interest(r)= 8 %p.a.
_21Maynewformat_files/20140521155159_image024.gif)
Maturity value= Rs (400 x n)+![]()
Given maturity value= Rs 16,176
Then Rs (400 x n)+![]() = Rs 16,176
= Rs 16,176
![]() 1200n + 4n2 + 4n = Rs 48,528
1200n + 4n2 + 4n = Rs 48,528
![]() 4n2 + 1204n = Rs 48,528
4n2 + 1204n = Rs 48,528
![]() n2 + 301n - 12132 = 0
n2 + 301n - 12132 = 0
![]() (n + 337)(n - 36)=0
(n + 337)(n - 36)=0
![]() n = -337 or n = 36
n = -337 or n = 36
Then number of months = 36 months = 3 years Ans.
Solution 5
Let installment per month = Rs P
Number of months(n) = 2 × 12 = 24
Rate of interest = 8%p.a.
_21Maynewformat_files/20140521155159_image035.gif)
Maturity value= Rs (P x 24) + Rs 2P = Rs 26P
Given maturity value = Rs 30,000
_21Maynewformat_files/20140521155159_image037.gif)
Solution 6
Let the monthly instalment be P
Interest = Rs. 8,325
Rate of interest = 7.5%
Time = 3 years = 36 months
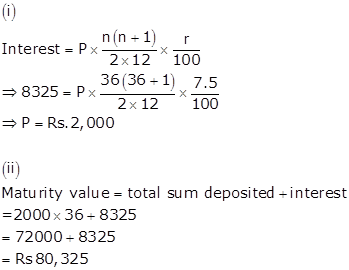
Solution 7
Installment per month(P) = Rs 900
Number of months(n) = 48
Let rate of interest(r) = r %p.a.

Maturity value= Rs (900 x 48) + Rs (882)r
Given maturity value = Rs 52,020
Then Rs (900 x 48) + Rs(882)r = Rs 52,020
![]() 882r = Rs 52,020 - Rs 43,200
882r = Rs 52,020 - Rs 43,200
![]() r =
r = ![]()
Solution 8
Let the value of the monthly installment be Rs. P.

Thus, the value of his monthly installment is Rs. 200.
Solution 9

Solution 10


