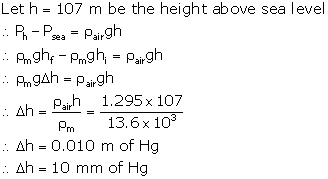Class 9 SELINA Solutions Physics Chapter 4: Pressure in Fluids and Atmospheric Pressure
Pressure in Fluids and Atmospheric Pressure Exercise Ex 4(A)
Solution A.1
(c) thrust
Solution A.2
(c) equal to the weight of the body
The thrust exerted by a body placed on a surface is equal to the weight of the body.
Solution A.3
(c) Newton
Solution A.4
(a) less on large area, more on small area
Solution A.5
(d) both (b) and (c)
The pressure exerted on a surface depends on the area on which the thrust is applied as well as on the magnitude of the thrust applied.
Solution A.6
(c) scalar and vector quantities respectively
Solution A.7
(b) Pa
Solution A.8
(c) dyne cm-2
Solution A.9
(c) 105 Nm-2
1 bar = 105 Nm-2
Solution A.10
(b) 760 torr
1 atm = 760 torr
Solution A.11
(b) increasing the area of surface
The pressure and the area are inversely proportional to each other.
Thus, pressure on a surface is reduced by increasing the area of surface.
Solution A.12
(d) small, high
Cutting tools have either sharp or pointed edges so that a small thrust may cause a high pressure at the edges and cutting can be done with less effort.
Solution A.13
(a) h ![]() g
g
Solution A.14
(d) It increases with an increase in the density of the liquid.
Solution A.15
(c) P1 ![]() P2
P2
Solution A.16
(d) P2 ![]() P1 = h
P1 = h ![]() g
g
Solution A.17
(c) the pressure exerted by a liquid
The wall of a dam is made thicker at the bottom so that it can withstand the higher pressure exerted by water.
Solution A.18
(c) Pascal's law
Hydraulic machines work on the principle of Pascal's law.
Solution A.19
(c) force multiplier
Hydraulic machines act like a force multiplier.
Solution B.1
Thrust is the force acting normally on a surface.
Its S.I. unit is 'newton'.
Solution B.2
(a) Pressure is measured in 'bar'.
(b) 1 bar = 105 pascal.
Solution B.3
One pascal is the pressure exerted on a surface of area 1 m2 by a force of 1N acting normally on it.
Solution B.4
Thrust is a vector quantity.
Solution B.5
Pressure is a scalar quantity.
Solution B.6
A substance which can flow is called a fluid.
Solution B.7
(a) P2 = P 1 + h ![]() g ,
g ,
(b) P2 ![]() P 1
P 1
Solution B.8
(i) As the diver moves to a greater depth, pressure exerted by sea water on him also increases.
(ii) When the diver moves horizontally, his depth from the free surface remains constant and hence the pressure on him remains unchanged.
Solution B.9
Pascal's law states that the pressure exerted anywhere in a confined liquid is transmitted equally and undiminished in all directions throughout the liquid.
Solution B.10
Two applications of Pascal's law:
(i) Hydraulic press
(ii) Hydraulic jack
Solution B.11
(a) h ![]() g (b) same (c) the same (d) directly proportional (e) directly proportional.
g (b) same (c) the same (d) directly proportional (e) directly proportional.
Solution C.1
Pressure is the thrust per unit area of the surface.
Its S.I. unit is 'newton per metre2' or 'pascal'.
Solution C.2
Thrust is the force applied on a surface in a perpendicular direction and it is a vector quantity. The effect of thrust per unit area is pressure, and it is a scalar quantity.
Solution C.3
Pressure exerted by thrust is inversely proportional to area of surface on which it acts. Thus, larger the area on which the thrust acts, lesser is the pressure exerted by it.
Example: If we stand on loose sand, our feet sink into the sand, but if we lie on that sand, our body does not sink into the sand. In both the cases, the thrust exerted on the sand is equal (equal to the weight of the body). However, when we lie on sand, the thrust acts on a large area and when we stand, the same thrust acts on a small area.
Solution C.4
The tip of an allpin is made sharp so that large pressure is exerted at the sharp end and it can be driven into with less effort.
Solution C.5
(a) It is easier to cut with a sharp knife because even a small thrust causes great pressure at the edges and cutting can be done with less effort.
(b) Wide wooden sleepers are placed below the railway tracks so that the pressure exerted by the rails on the ground becomes less.
Solution C.6
Due to its weight, a fluid exerts pressure in all directions; the pressure exerted by the fluid is called fluid pressure.
Solution C.7
A solid exerts pressure only on the surface on which it is placed, i.e. at its bottom, but a fluid exerts pressure at all points in all directions.
Solution C.8
Pressure at a point in a liquid depends upon the following three factors:
(i) Depth of the point below the free surface.
(ii) Density of liquid.
(iii) Acceleration due to gravity.
Solution C.9
P = Po + h ![]() g
g
Here, P = Pressure exerted at a point in the liquid
Po = Atmospheric pressure
h = Depth of the point below the free surface
![]() = Density of the liquid
= Density of the liquid
g = Acceleration due to gravity
Solution C.10
Due to dissolved salts, density of sea water is more than the density of river water, so pressure at a certain depth in sea water is more than that at the same depth in river water.
Solution C.11
The reason is that when the bubble is at the bottom of the lake, total pressure exerted on it is the atmospheric pressure plus the pressure due to water column. As the gas bubble rises, due to decrease in depth the pressure due to water column decreases. By Boyle's law, PV = constant, so the volume of bubble increases due to decrease in pressure, i.e., the bubble grows in size.
Solution C.12
The pressure exerted by a liquid increases with its depth. Thus as depth increases, more and more pressure is exerted by water on wall of the dam. A thicker wall is required to withstand greater pressure, therefore, the thickness of the wall of dam increases towards the bottom.
Solution C.13
The sea divers need special protective suit to wear because in deep sea, the total pressure exerted on the diver's body is much more than his blood pressure. To withstand it, he needs to wear a special protective suit.
Solution C.14
Laws of liquid pressure:
(i) Pressure at a point inside the liquid increases with the depth from its free surface.
(ii) In a stationary liquid, pressure is same at all points on a horizontal plane.
(iii) Pressure is same in all directions about a point in the liquid.
(iv) Pressure at same depth is different in different liquids. It increases with the increase in the density of liquid.
(v) A liquid seeks its own level.
Solution C.15
The liquid from hole B reaches a greater distance on the horizontal surface than that from hole A.
This explains that liquid pressure at a point increases with the depth of point from the free surface.
Solution C.16
Hydraulic press works on principle of hydraulic machine.
It states that a small force applied on a smaller piston is transmitted to produce a large force on the bigger piston.
Use: It is used for squeezing oil out of linseed and cotton seeds.
Solution D.1
Take a can or large plastic bottle filled with water. Place it on a horizontal surface. Make a series of holes in the wall of the vessel anywhere below the free surface of the liquid. The water spurts out through each hole. This shows that the liquid exerts pressure at each point on the wall of the bottle.
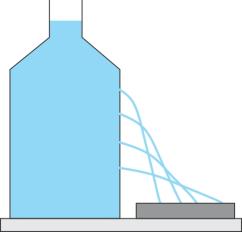
Liquid exerts pressure at all points in all directions
Solution D.2
Consider a vessel containing a liquid of density![]() . Let the liquid be stationary. In order to calculate pressure at a depth, consider a horizontal circular surface PQ of area A at a depth h below the free surface XY of the liquid. The pressure on the surface PQ will be due to the thrust of the liquid contained in cylinder PQRS of height h with PQ as its base and top face RS lying on the frees surface XY of the liquid.
. Let the liquid be stationary. In order to calculate pressure at a depth, consider a horizontal circular surface PQ of area A at a depth h below the free surface XY of the liquid. The pressure on the surface PQ will be due to the thrust of the liquid contained in cylinder PQRS of height h with PQ as its base and top face RS lying on the frees surface XY of the liquid.
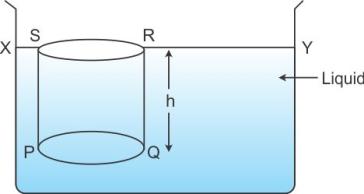
Total thrust exerted on the surface PQ
= Weight of the liquid column PQRS
= Volume of liquid column PQRS x density x g
= (Area of base PQ x height) x density x g
= (A x h) x ![]() x g
x g
This thrust is exerted on the surface PQ of area A. Therefore, pressure is given as shown below.
P = Thrust on surface / Area of surface
P = Ah![]() g / A = h
g / A = h![]() g
g
Thus, Pressure = depth x density of liquid x acceleration due to gravity
Solution D.3
The principle of a hydraulic machine is that a small force applied on a smaller piston is transmitted to produce a large force on the bigger piston.
Hydraulic press and hydraulic brakes work on this principle.
Solution D.4
(i) X : Press Plunger; Y: Pump Plunger
(ii) When the lever is moved down, valve B closes and valve A opens, so the water from cylinder P is forced into the cylinder Q.
(iii) Valve B closes due to an increase in pressure in cylinder P. This pressure is transmitted to the connecting pipe and when the pressure in connecting pipe becomes greater than the pressure in the cylinder Q, valve A opens up.
(iv) When the release valve is opened, the ram (or press) plunger Q gets lowered and water of the cylinder Q runs out in the reservoir.
v.When the lever arm is moved upward, valve B opens.
vi.Because the pressure in cylinder P decreases as the lever arm is moved up, valve B opens upward.
vii.A hydraulic press is used to press cotton bales and other items such as quilts and books.
Solution D.5
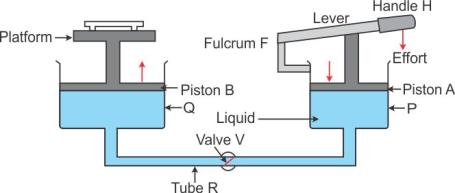
Working: When handle H of the lever is pressed down by applying an effort, the valve V opens because of increase in pressure in cylinder P. The liquid runs out from the cylinder P to the cylinder Q. As a result, the piston B rises up and it raises the car placed on the platform. When the car reaches the desired height, the handle H of the lever is no longer pressed. The valve V gets closed (since the pressure on the either side of the valve becomes same) so that the liquid may not run back from the cylinder Q to cylinder P.
Solution D.6
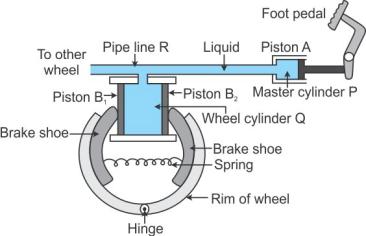
Working: To apply brakes, the foot pedal is pressed due to which pressure is exerted on the liquid in the master cylinder P, so liquid runs out from the master cylinder P to the wheel cylinder Q. As a result, the pressure is transmitted equally and undiminished through the liquid to the pistons B1 and B2 of the wheel cylinder. Therefore, the pistons B1 and B2 get pushed outwards and brake shoes get pressed against the rim of the wheel due to which the motion of the vehicle retards. Due to transmission of pressure through the liquid, equal pressure is exerted on all the wheels of the vehicle connected to the pipe line R.
On releasing the pressure on the pedal, the liquid runs back from the wheel cylinder Q to the master cylinder P and the spring pulls the break shoes to their original position and forces the pistons B1 and B2 to return back into the wheel cylinder Q. Thus, the brakes get released.
Solution E.1
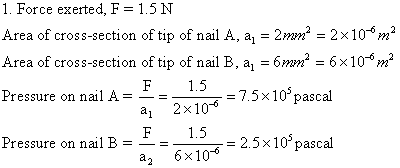
Solution E.2

Solution E.3

Solution E.4

Solution E.5

![]()
Solution E.6

Solution E.7

Solution E.8
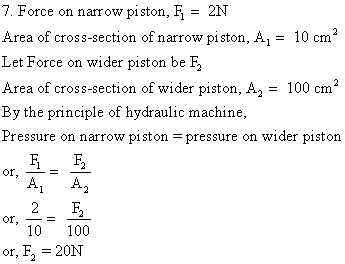
Solution E.9

Solution E.10
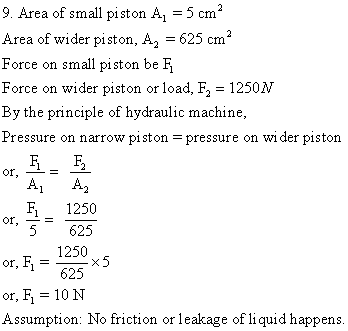
Solution E.11

Solution E.12

Solution E.13
i) Given that the force applied to the smaller piston A is 4 kg
Area of cross section of piston A = 8 cm²
Area of cross section of piston B = 320 cm²
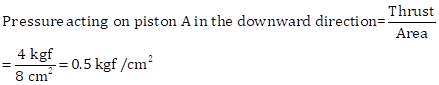
ii) According to Pascal's law,
Pressure acting on piston B = Pressure acting on piston A = 0.5 kgf/cm2
iii) Thrust acting on piston B in the upward direction
= Pressure × Area of B
= 4 kgf × 320/8
Thus,
Thrust acting on piston B in upward direction = 160 kgf
Solution E.14
In a hydraulic machine
Pressure on narrow piston = Pressure on wider piston
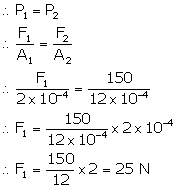
Pressure in Fluids and Atmospheric Pressure Exercise Ex 4(B)
Solution A.1
(b) atmospheric pressure
Solution A.2
(b) 76 cm of Hg
Solution A.3
(c) 1 torr = 1 mm of Hg
Solution A.4
(c) P1 < P2
Solution A.5
(c) the blood pressure becomes more than the atmospheric pressure
Solution A.6
(c) Torricelli
Solution A.7
(d) all of the above
A barometer is used to measure atmospheric pressure, for weather forecasting, as an altimeter to measure heights.
Solution A.8
(c) only 30% of the atmospheric pressure at sea level
Solution A.9
(a) less
At high altitudes, the atmospheric pressure is less.
Solution A.10
(d) all of the above
Mercury is preferred as a barometric
Solution A.11
(a) It neither wets nor sticks to the glass tube
Solution A.12
(d) a possibility of rain
Solution A.13
(c) P l ![]() P2
P2
Solution A.14
(b) altitudes
Solution B.1
1.013 x 10 5 pascal
Solution B.2
Atmospheric pressure is measured in 'torr'.
1 torr = 1 mm of Hg.
Solution B.3
At normal temperature and pressure, the barometric height is 0.76 m of Hg at sea level which is taken as one atmosphere.
1 atmosphere = 0.76 m of Hg = 1.013 x 105 pascal
Solution B.4
When a vacuum is created in the bell jar, initially the pressure in the bell jar will be lower than that in the balloon.
Thus, the balloon expands.
This means the pressure inside the balloon increases while the pressure inside the bell jar decreases.
a) decreases
b) increases
Solution B.5
A barometer is used to measure atmospheric pressure.
Solution B.6
The atmospheric pressure at a place is 76 cm of Hg means at normal temperature and pressure, the height of the mercury column supported by the atmospheric pressure is 76 cm.
76 cm of Hg = 1.013 x 105 pascal
Solution B.7
(a) The barometric height remains unaffected.
(b) The barometric height remains unaffected.
(c) The barometric height decreases.
Solution B.8
Two uses of barometer:
(a) To measure the atmospheric pressure.
(b) For weather forecasting
Solution B.9
(i) In a mine, reading of a barometer increases.
(ii) On hills, reading of barometer decreases.
Solution B.10
(a) It indicates that the moisture is increasing i.e., there is a possibility of rain.
(b) It indicates the coming of a storm or cyclone.
(c) It indicates that the moisture is decreasing i.e., it indicates dry weather.
Solution C.1
The thrust exerted per unit area of the earth surface due to column of air, is called the atmospheric pressure on the earth surface.
Solution C.2
We do not feel uneasy under enormous pressure of the atmosphere above as well as around us because of the pressure of our blood, known as blood pressure, is slightly more than the atmospheric pressure. Thus, our blood pressure balances the atmospheric pressure.
Solution C.3
Experiment to demonstrate that air exerts pressure:
Take a thin can fitted with an airtight stopper. The stopper is removed and a small quantity of water is boiled in the can. Gradually the steam occupies the entire space of can by expelling the air from it [Fig (a)]. Then stopper is then tightly replaced and simultaneously the flame beneath the can is removed. Cold water is then poured over the can.
It is observed that the can collapses inwards as shown in fig (b).
The reason is that the pressure due to steam inside the can is same as the air pressure outside the can [Fig (a)]. However, on pouring cold water over the can, fitted with a stopper [fig (b)], the steam inside the can condenses producing water and water vapour at very low pressure. Thus, the air pressure outside the can becomes more than the vapour pressure inside the closed can.
Consequently, the excess atmospheric pressure outside the can causes it to collapse inwards.
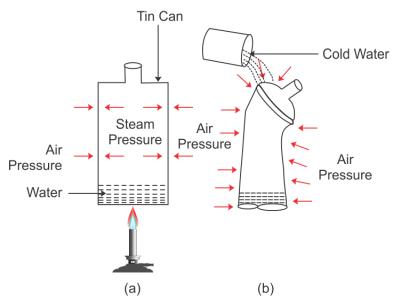
Solution C.4
(i)When air is removed from the balloon, the pressure inside the balloon (which was due to air in it) is much less than the atmospheric pressure outside and hence the balloon collapses.
(ii) Water is held inside the dropper against the atmospheric pressure because the pressure due to height column of liquid inside the dropper is less than the atmospheric pressure. By pressing the dropper we increase the pressure inside the dropper and when it becomes greater than the atmospheric pressure the liquid comes out of the dropper.
(iii) There is no air inside a completely filled and sealed can. When a single hole is made to drain out the oil from the can, some of the oil will come out and due to that the volume of air above the oil will increase and hence the pressure of air will decrease. But if two holes are made on the top cover of the can, air outside the can will enter it through one hole and exert atmospheric pressure on the oil from inside along with the pressure due to oil column, and it will come out of the can from the other hole.
Solution C.5
When syringe is kept with its opening just inside a liquid and its plunger is pulled up in the barrel, the pressure of air inside the barrel below the plunger becomes much less than the atmospheric pressure acting on the liquid. As a result, the atmospheric pressure forces the liquid to rise up in the syringe.
Solution C.6
In a water pump, on pulling the piston up, the pressure of air inside the siphon decreases and the atmospheric pressure on the water outside increases. As a result, the atmospheric pressure pushes the water up in pump.
Solution C.7
In given figure, at all points such as C on the surface of mercury in trough, only the atmospheric pressure acts. When the mercury level in the tube becomes stationary, the pressure inside tube at the point A, which is at the level of point C, must be same as that at the point C. The pressure at point A is due to the weight (or thrust) of the mercury column AB above it. Thus, the vertical height of the mercury column from the mercury surface in trough to the level in tube is a measure of the atmospheric pressure.
The vertical of the mercury column in it (i.e., AB = h) is called the barometric height.
Had the pressure at points A and C be not equal, the level of mercury in the tube would not have been stationary.
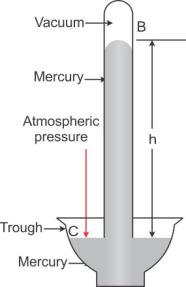
Solution C.8
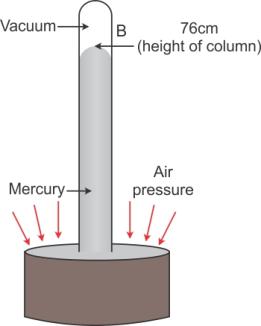
Solution C.9
It is the atmospheric pressure acting on the surface of the mercury in the trough that supports the vertical mercury column. Hence, barometric height is used as unit to express the atmospheric pressure.
Solution C.10
The space above mercury is a vacuum. This empty space is called 'Torricellian vacuum'.
This can be shown by tilting the tube till the mercury fills the tube completely. Again when the mercury column becomes stationary, the empty space is created above the mercury column. If somehow air enters into the empty space or a drop of water gets into the tube, it will immediately vaporize and the air will exert pressure on mercury column due to which the barometric height will decrease.
Solution C.11
Two advantages of using mercury as barometric liquid:
(i) The density of mercury is greater than that of all the liquids, so only 0.76m height of mercury column is needed to balance the normal atmospheric pressure.
(ii) The mercury neither wets nor sticks to the glass tube therefore it gives the correct reading.
Solution C.12
Water is not a suitable barometric liquid because:
(i) The vapour pressure of water is high, so its vapours in the vacuum space will make the reading inaccurate.
(ii) Water sticks with the glass tube and wets it, so the reading becomes inaccurate.
Solution C.13
Aneroid barometer has no liquid and it is portable. It is calibrated to read directly the atmospheric pressure.
Solution C.14
The atmospheric pressure decreases with an increase in the altitude.
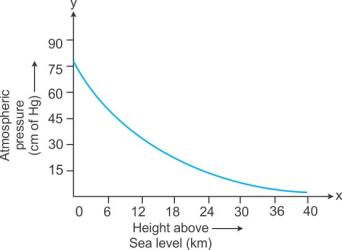
Solution C.15
Factors that affect the atmospheric pressure are:
(i) Height of air column
(ii) Density of air
Solution C.16
A fountain pen filled with ink contains some air at a pressure equal to atmospheric pressure on earth's surface. When pen is taken to an altitude, atmospheric pressure is low so the excess pressure inside the rubber tube forces the ink to leak out.
Solution C.17
On mountains, the atmospheric pressure is quite low. As such, nose bleeding may occur due to excess pressure of blood over the atmospheric pressure.
Solution D.1
A barometer is an instrument which is used to measure the atmospheric pressure.
Construction of a simple barometer:
A simple mercury barometer can be made with a clear, dry, thick-walled glass tube about 1 metre ling. The glass tube is sealed at one end and is filled with mercury completely. While filling the tube with mercury care has to be taken so that there are no air bubbles present in the mercury column. Close the open end with thumb and turn the tube upside down carefully over a trough containing mercury. Dip the open end under the mercury level in the trough and remove the thumb.
The mercury level in the tube falls until it is about 76 cm (h =760 mm) vertically above the mercury level. It is the atmospheric pressure acting on the surface of the mercury in the trough that supports the vertical mercury column. The empty space above the mercury column is called the 'Torricellian vacuum'.
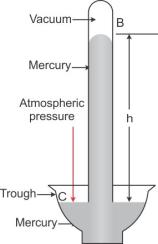
Solution D.2
In a simple barometer, there is no protection for the glass tube but in Fortin's barometer, this defect has been removed by enclosing the glass tube in a brass case.
In a simple barometer, a scale cannot be fixed with the tube (or it cannot be marked on the tube) to measure the atmospheric pressure but Fortin's barometer is provided with a vernier calipers to measure the accurate reading.
Solution D.3
An altimeter is a device used in aircraft to measure its altitude.
Principle: Atmospheric pressure decreases with the increase in height above the sea level; therefore, a barometer measuring the atmospheric pressure can be used to determine the altitude of a place above the sea level.
The scale of altimeter is graduated with height increasing towards left because the atmospheric pressure decreases with increase of height above the sea level.
Solution D.4
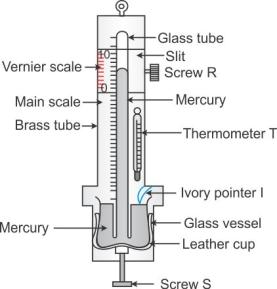
To measure the atmospheric pressure, first the leather cup is raised up or lowered down with the help of the screw S so that the ivory pointer I just touches the mercury level in the glass vessel. The position of the mercury level in the barometer tube is noted with the help of main scale and the vernier scale. The sum of the vernier scale reading to the main scale reading gives the barometric height.
Solution D.5
A barometer calibrated to read directly the atmospheric pressure is called an aneroid barometer. It has no liquid, it is light and portable.
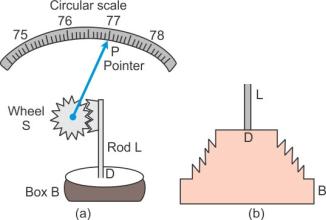
Construction: Figure above shows the main parts of an aneroid barometer. It consists of a metallic box B which is partially evacuated. The top D of the box is springy and corrugated in form of a diaphragm as shown. At the middle of diaphragm, there is a thin rod L toothed at its upper end. The teeth of rod fit well into the teeth of a wheel S attached with a pointer P which can slide over a circular scale. The circular scale is initially calibrated with a standard barometer so as to read the atmospheric pressure directly in terms of the barometric height.
Working: When atmospheric pressure increases, it presses the diaphragm D and the rod L gets depressed. The wheel S rotates clockwise and pointer P moves to the right on the circular scale. When atmospheric pressure decreases, the diaphragm D bulges out due to which the rod L moves up and the wheel S rotates anti-clockwise. Consequently, the pointer moves to the left.
Solution E.1
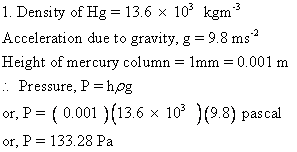
Solution E.2

Solution E.3

Assumption: Atmospheric pressure falls linearly with ascent.
Solution E.4
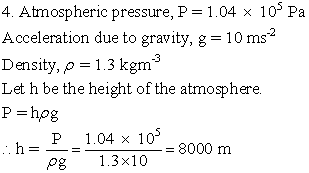
Solution E.5