Class 9 SELINA Solutions Physics Chapter 2: Motion in One Dimension
Motion in One Dimension Exercise Ex 2(A)
Solution A.1
a) Scalar quantities
Solution A.2
(b) Time
Solution A.3
(c) Both (a) and (b)
A vector quantity possesses both direction as well as magnitude.
Solution A.4
(d) Velocity
Velocity is a vector quantity. The others are all scalar quantities.
Solution A.5
(c) One-dimensional
The motion of a train on a straight track is an example of one - dimensional motion
Solution A.6
d) Metre
The S.I. unit of displacement is metre.
Solution A.7
c) 0 m
As the final and the initial position of the body is same, the displacement if the body is 0.
Solution A.8
(c) Variable acceleration
Motion of a car in a crowded street is an example of variable acceleration.
Solution A.9
(a) 100 m
Time(t) = 10s
Speed(v) = 10 ms⁻¹
We know
Distance = Speed × Time
d = v × t
d = 10 × 10
d = 100 m
Solution A.10
(a) Displacement
Solution A.11
(d) m s-1
Solution A.12
(b) m s-2
Solution A.13
(b) 5 m s-1
Solution A.14
(d) All of the above
The value of g does not depend on the Height of the body, Mass of the body and shape of the body.
Solution A.15
(a) Uniform acceleration
Solution A.16
(d) Poles
Solution A.17
(d) The displacement is zero.
Solution B.1
a) Pressure is a scalar quantity.
b) Momentum is a vector quantity.
c) Weight is a vector quantity.
d) Force is a vector quantity.
e) Energy is a scalar quantity.
f) Speed is a scalar quantity.
Solution B.2
Scalar quantities are expressed by
i) Magnitude or numerical value of measured quantity
ii) Unit in which the physical quantity is measured
Solution B.3
Scalar quantities are expressed by
i) Magnitude or numerical value of measured quantity
ii) Unit in which the physical quantity is measured
iii) Direction
Solution B.4
The negative sign with a vector quantity indicates the opposite or reverse direction.
Solution B.5
A body is said to be at rest if it does not change its position with respect to its immediate surroundings.
Solution B.6
A body is said to be in motion if it changes its position with respect to its immediate surroundings.
Solution B.7
When a body moves along a straight line path, its motion is said to be one-dimensional motion.
Solution B.8
The shortest distance from the initial to the final position of the body is called the magnitude of displacement. It is in the direction from the initial position to the final position.
Its SI unit is metre (m).
Solution B.9
The magnitude of displacement is equal to distance if the motion of the body is one-dimensional.
Solution B.10
The velocity of a body is the distance travelled per second by the body in a specified direction.
Its SI unit is metre/second (m/s).
Solution B.11
The speed of a body is the rate of change of distance with time.
Its SI unit is metre/second (m/s).
Solution B.12
Velocity gives the direction of motion of the body.
Solution B.13
Instantaneous velocity is equal to average velocity if the body is in uniform motion.
Solution B.14
Acceleration is the rate of change of velocity with time.
Its SI unit is metre/second2 (m/s2).
Solution B.15
Retardation is the decrease in velocity per second.
Its SI unit is metre/second2 (m/s2).
Solution B.16
Velocity determines the direction of motion.
Solution B.17
When a body falls freely under gravity, the acceleration produced in the body due to the Earth's gravitational acceleration is called the acceleration due to gravity (g). The average value of g is 9.8 m/s2.
Solution C.1
|
Scalar |
Vector |
|
They are expressed only by their magnitudes. |
They are expressed by magnitude as well as direction. |
|
They can be added, subtracted, multiplied or divided by simple arithmetic methods. |
They can be added, subtracted or multiplied following a different algebra. |
|
They are symbolically written by English letter. |
They are symbolically written by their English letter with an arrow on top of the letter. |
|
Example: mass, speed |
Example: force, velocity |
Solution C.2
- A scalar is a quantity that has magnitude but no definite direction.
- A vector is a quantity that has magnitude and acts in a specific direction.
- As a result, vector quantities cannot be added using the arithmetic rule because they have direction.
Solution C.3(a)
Distance is a scalar quantity, while displacement is a vector quantity. The magnitude of displacement is either equal to or less than the distance. The distance is the length of path travelled by the body so it is always positive, but the displacement is the shortest length in direction from initial to the final position so it can be positive or negative depending on its direction. The displacement can be zero even if the distance is not zero.
Solution C.3(b)
Speed is a scalar quantity, while velocity is a vector quantity. The speed is always positive-it is the magnitude of velocity, but the velocity is given a positive or negative sign depending upon its direction of motion. The average velocity can be zero but the average speed is never zero.
Solution C.3(c)
If a body travels equal distances in equal intervals of time along a particular direction, then the body is said to be moving with a uniform velocity. However, if a body travels unequal distances in a particular direction in equal intervals of time or it moves equal distances in equal intervals of time but its direction of motion does not remain same, then the velocity of the body is said to be variable (or non-uniform).
Solution C.3(d)
Average speed is the ratio of the total distance travelled by the body to the total time of journey, it is never zero. If the velocity of a body moving in a particular direction changes with time, then the ratio of displacement to the time taken in entire journey is called its average velocity. Average velocity of a body can be zero even if its average speed is not zero.
Solution C.3(e)
Acceleration is the increase in velocity per second, while retardation is the decrease in velocity per second. Thus, retardation is negative acceleration. In general, acceleration is taken positive, while retardation is taken negative.
Solution C.3(f)
The acceleration is said to be uniform when equal changes in velocity take place in equal intervals of time, but if the change in velocity is not the same in the same intervals of time, the acceleration is said to be variable.
Solution C.4
Yes, displacement can be zero even if the distance is not zero.
For example, when a body is thrown vertically upwards from a point A on the ground, after sometime it comes back to the same point A. Then, the displacement is zero, but the distance travelled by the body is not zero (it is 2h; h is the maximum height attained by the body).
Solution C.5
The motion of a body in a circular path with uniform speed has a variable velocity because in the circular path, the direction of motion of the body continuously changes with time.

Solution C.6
If a body starts its motion from a point and comes back to the same point after a certain time, then the displacement is zero, average velocity is also zero, but the total distance travelled is not zero, and therefore, the average speed in not zero.
Solution C.7
(a) Example of uniform velocity: A body, once started, moves on a frictionless surface with uniform velocity.
(b) Example of variable velocity: A ball dropped from some height is an example of variable velocity.
(c) Example of variable acceleration: The motion of a vehicle on a crowded road is with variable acceleration.
(d) Example of uniform retardation: If a car moving with a velocity 'v' is brought to rest by applying brakes, then such a motion is an example of uniform retardation.
Solution C.8
Initially as the drops are equidistant, we can say that the car is moving with a constant speed but later as the distance between the drops starts decreasing, we can say that the car slows down.
Solution C.9
In circular motion, at any instant, the direction of velocity is tangential to the circular path at the point.
Solution C.10
No. The value of 'g' varies from place to place. It is maximum at poles and minimum at the Equator on the surface of the Earth.
Solution C.11
In vacuum, both will reach the ground simultaneously because acceleration due to gravity is same (=g) on both objects.
Solution D.1
Speed of car = 72 km h-1
Speed of car in ms-1
= ![]()
Solution D.2

Solution D.3

Solution D.4
18 km h-1 < 10 m s-1 < 1 km min-1
Solution D.5
Total time taken = 3 hours
Speed of the train = 65 km/hr
Distance travelled = speed x time
= 65 x 3 = 195 km
Solution D.6
For the first 30 km travelled, speed = 60 km/h.
Thus time taken (t1) = Distance / speed
= (30/60) h-1
= 0.5 h-1 or 30 min.
For the next 30 km travelled, speed = 40 km/h
Thus time taken (t2) = Distance/speed
= (30/40) h-1
= 0.75 h-1 or 45 min.
(i) Total time = (30 + 45) min
= 75 min or 1.25 h.
(ii) Average speed of the car = Total distance travelled/total time taken
![]()
Solution D.7
Here, total distance = (200 + 200) km = 400 km
Total time taken = (2 + 3) h = 5 h
(i) Average speed = Total distance travelled/total time taken
![]()
(ii) Average velocity of the train is zero because the train stops at the same point from where it starts, i.e. the displacement is zero.
Solution D.8
(i) Speed of the car = Distance/time taken
![]()
(ii) Velocity of car = Speed with direction
= 10 m/s due east
Solution D.9
Here, final velocity = 10 m/s
Initial velocity = 0 m/s
Time taken = 2s
Acceleration = (Final Velocity - Initial Velocity)/time
= (10/2) ms-2
= 5 ms-2
Solution D.10
Here, final velocity = 180 m/s
Initial velocity = 0 m/s
Time taken = 0.05 h or 180 s
Acceleration = (Final Velocity - Initial Velocity)/time
= (180-0)/180 m s-2
= 1 m s-2
Solution D.11
Here, final velocity = 20 m/s
Initial velocity = 50 m/s
Time taken = 3 s
Acceleration = (Final Velocity - Initial Velocity)/time
= (20 - 50)/3 m/s2
= -10 m/s2
Negative sign here indicates that the velocity decreases with time, so retardation is 10 m/s2.
Solution D.12
Here, final velocity = 18 km/h or 5 m/s
Initial velocity = 0 km/h
Time taken = 2 s
Acceleration = (Final Velocity - Initial Velocity)/time
= (5 - 0) / 2 m s-2
= 2.5 m s-2
Solution D.13
Acceleration = Increase in velocity/time taken
Therefore, increase in velocity = Acceleration × time taken
= (5 × 2) m/s
= 10 m/s
Solution D.14
Initial velocity of the car, u = 20 m/s
Retardation = 2 m/s2
Given time, t = 5 s
Let 'v' be the final velocity.
We know that, Acceleration = Rate of change of velocity /time
= (Final velocity - Initial velocity)/time
Or, -2 = (v - 20) / 5
Or, -10 = v - 20
Or, v = -20 + 10 m/s
Or, v = -10 m/s
Negative sign indicates that the velocity is decreasing.
Solution D.15
Initial velocity of the bicycle, u = 5 m/s
Acceleration = 2 m/s2
Given time, t = 5 s
Let 'v' be the final velocity.
We know that, acceleration = Rate of change of velocity/time
= (Final velocity - Initial velocity)/time
Or 2 = (v - 5)/5
Or, 10 = (v - 5)
Or, v = 5 + 10
Or, v = 15 m/s
Solution D.16
Initial velocity of the bicycle, u = 18 km/hr
Time taken, t = 5 s-1
Final velocity, v = 0 m/s (As the car comes to rest)
(i) Speed in m/s ![]()
(ii) Retardation = (Final velocity - Initial velocity)/time taken
Or, Retardation = ![]()
(iii) Let 'V' be the speed of the car after 2 s of applying the brakes.
Then, Acceleration = (V - 5)/ 2
Or, -1 = (V - 5)/2
Or, V = -2 + 5
Or, V = 3 m/s
Motion in One Dimension Exercise Ex 2(B)
Solution A.1
(a) Velocity
Solution A.2
i. (a) uniform
ii. (c) 10 ms-1
iii. (c) 40 m
Solution A.3
b)
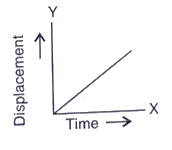
Solution A.4
(c) Both (a) and (b)
Solution A.5
(b) Displacement
Velocity = displacement /time
Thus,
Velocity x time = displacement
Solution A.6
(b) Acceleration is uniform.
Solution A.7
(d) A straight line inclined to the time axis.
Solution A.8
(i) (c) 125 m
Now, for the given graph:
Distance travelled in 5 sec, d = ½ × base × height
∴ d = ½ × 5× 50 = 125 m
(ii) (c) 10 m/s-2
As we know,
Retardation or negative acceleration for the given case will be:
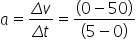
Solution A.9
d)

Solution A.10
(c)
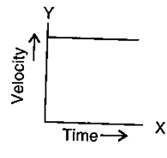
Solution A.12
(d) Acceleration
Solution A.13
(b) 1/4
Now, as we know,
Distance travelled = Total area under v-t curve,
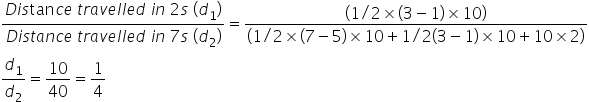
Solution A.14
(a) 8 m, 16 m
Now as we know,
Displacement (d)=Area under v-t curve
Solution B.1
For the motion with uniform velocity, distance is directly proportional to time.
Solution B.2
Slope of a displacement-time graph represents velocity.
Solution B.3
For motion in one direction, in a straight line, if the body does not return i.e., it does not move in the opposite direction, then distance - time graph and displacement - time graph are same.
Solution B.4
The slope of displacement - time graph gives velocity. Greater slope (more inclination of straight line) of displacement - time graph indicates that the velocity is higher.
Solution B.5
The slope of displacement - time graph gives velocity. The negative slope indicates that the body is returning towards the starting point (or reference point).
Solution B.6
The slope of the velocity-time graph represents acceleration.
Solution B.7
The slope of velocity - time graph gives the acceleration. The larger slope of velocity - time graph means higher is the acceleration or retardation of the object or body.
Solution B.8
The negative slope of velocity - time graph means that the velocity is decreasing, and the object is under the retardation (negative acceleration).
Solution C.1
From displacement-time graph, the nature of motion (or state of rest) can be understood. The slope of this graph gives the value of velocity of the body at any instant of time, using which the velocity-time graph can also be drawn.
Solution C.2
The displacement-time graph can never be parallel to the displacement axis because such a line would mean that the distance covered by the body in a certain direction increases without any increase in time, which is not possible.
Solution C.3
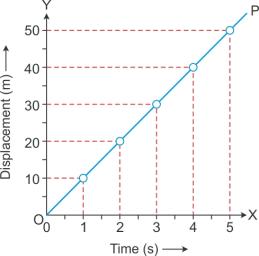
Solution C.4
(i) The slope of the velocity-time graph gives the value of acceleration.
(ii) The total distance travelled by a body in a given time is given by the area enclosed between the velocity-time graph and X-axis (without any sign).
(iii) The displacement of a body in a given time is given by the area enclosed between the velocity-time graph and X-axis (with proper signs).
Solution C.5
(a) There is no motion, the body is at rest.
(b) It depicts that the body is moving away from the starting point with uniform velocity.
(c) It depicts that the body is moving towards the starting point with uniform velocity.
(d) It depicts that the body is moving with variable velocity.
Solution C.6
Vehicle A is moving with a faster speed because the slope of line A is more than the slope of line B.
Solution C.7
The body moving with a varying speed in a fixed direction is variable velocity.
The velocity at such instant can be obtained by finding the slope or the gradient of the tangent drawn on the curve at that instant of time.
Solution C.8
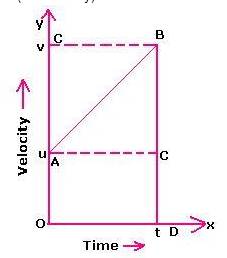
In this graph, initial velocity = u
Velocity at time t = v
Let acceleration be 'a'
Time = t
Then, distance travelled by the body in t s = area between the v-t graph and X-axis
Or distance travelled by the body in t s = area of the trapezium OABD
= (1/2) × (sum of parallel sides) × (perpendicular distance between them)
= (1/2) × (u + v) × (t)
= (u + v)t /2
Solution C.9
(a) Fig. 4.33 (a) represents uniformly accelerated motion. For example, the motion of a freely falling object.
(b) Fig. 4.33 (b) represents motion with variable retardation. For example, a car approaching its destination.
Solution C.10
Car B has greater acceleration because the slope of line B is more than the slope of line A.
Solution C.11

Velocity-time for a body moving with uniform velocity and uniform acceleration.
Solution C.12
retardation is calculated by finding the negative slope.
Solution C.13
For body A: The graph is a straight line. So, the slope gives constant velocity. Hence, the acceleration for body A is zero.
For body B: The graph is a straight line. So, the slope gives constant velocity. Hence, the acceleration for body B is also zero.
For body C: The slope of the graph is decreasing with time. Hence, the acceleration is negative.
For body D: The slope of the graph is increasing with time. Hence, the acceleration is positive.
Solution C.14
The area enclosed between the straight line and time axis for each interval of time gives the value of change in speed in that interval of time.
Solution C.15
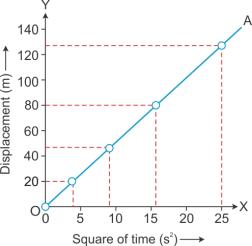
Solution C.16
For motion under uniform acceleration, such as the motion of a freely falling body, distance is directly proportion to the square of the time.
Solution C.17
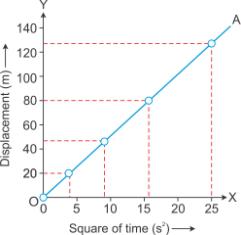
The value of acceleration due to gravity (g) can be obtained by doubling the slope of the ![]() graph for a freely falling body.
graph for a freely falling body.
Solution D.1
a) Velocity - time graph for a uniform velocity:
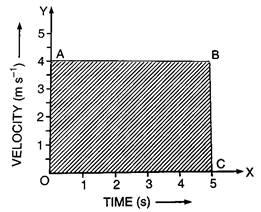
Here the body is motion with uniform velocity. The velocity - time graph is a straight line parallel to the time axis.
A straight-line AB represents the velocity - time graph of a body moving with a uniform velocity 4 m/s for 5 s.
Thus, displacement = velocity × time = 4 × 5 = 20 m.
b) Velocity - time graph for a uniform acceleration:

The velocity is increasing by an equal amount in the given graph. This indicates that the body is moving with uniform acceleration.
Distance travelled by body in 8 seconds is,
S = area of triangle OPQ = ½ x base x height = ½ x 8 s x 80 m/s = 320 m
Acceleration of body = slope of the line OP = PQ/QO = (80 - 0)/(8 - 0) = 80 ms-1/ 8 = 10 m/s2
Solution D.2
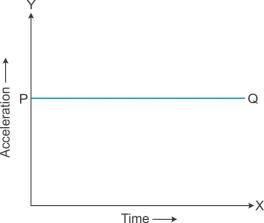
a) Acceleration - time graph for a body moving with uniform velocity
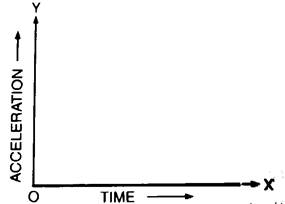
For example, when a body is at rest or is moving with uniform velocity, the acceleration - time graph is straight line coinciding with the time axis.
b)
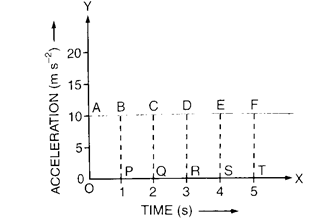
For example, body falling under the gravity moves with a uniform acceleration.
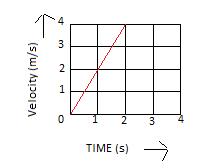
Solution E.1
Velocity of body at t = 1s is 2 m/s
Velocity of body at t = 2s is 4 m/s
Velocity of body at t = 3s is 6 m/s
Solution E.2
(a)
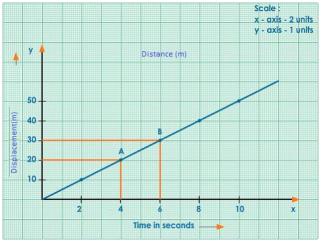
Displacement-time graph
From the part AB of the graph,
Average velocity = (Displacement at B - Displacement at A)/Time taken
= (30 - 20) m/( 6 - 4) s
= (10/2) m/s
= 5 m/s
(b) (i) From the graph, the displacement of car at 2.5 s is 12.5 m.
(ii) From the graph, the displacement of car at 4.5 s is 22.5 m.
Solution E.3
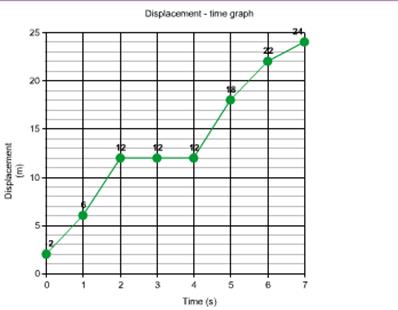
(i) Total distance travelled in interval 1s to 5s = 18m - 6m = 12 m.
(ii) Average velocity = Total displacement in the given time interval/Time interval, i.e. 1 s to 5 s.
Or, Average velocity = 12 m/4 s = 3 m/s.
Solution E.4
(a) (i) Velocity from 0 to 5 s = Displacement /time
= (3/5) m/s
= 0.6 m/s-1
(ii) Velocity from 5 s to 7 s = Displacement /time
= (0/2) m/s
= 0 m/s-1.
(iii) Velocity from 7 s to 9 s = Displacement /time
= (7 - 3)/(9 - 7) m/s
= (4/2) m/s
= 2 m/s-1
(b) From, 5 s to 9 s, displacement = 7m - 3m = 4m.
Time elapsed between 5 s to 9 s = 4 s
Average velocity = Displacement/time
= (4/4) m/s
= 1 m/s-1
Solution E.5
(i) Displacement in first 4s = 10 m
Therefore, the average velocity = Displacement/time
= (10/4) m/s
= 2.5 m/s-1
(ii) Initial position = 0 m
Final position at the end of 10 s = -10m
Displacement = Final position - Initial position
= (-10) m - 0
= -10 m
(iii) At 7 s and 13 s, the cyclist reaches his starting point.
Solution E.6
(i) Initially, the car B was 40 km ahead of car A.
(ii) Straight line depicts that cars A and B are moving with uniform velocities.
For car A
Displacement at t = 1 h is 40 m
Velocity = Displacement /time
= (40/1) km/h
= 40 km/h-1
For car B
Displacement at t = 4 h is (120 - 40) km, i.e. 80 km
Velocity = Displacement /time
= (80/4) km/h
= 20 km/h-1
(iii) Car A catches car B in 2 hours.
(iv) After starting, car A will catch car B at 80 km.
Solution E.7
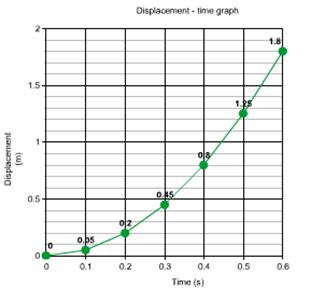
The graph is curve therefore the motion is with non-uniform velocity.
Solution E.8
Velocity of the body at t = 1 s is 1 m/s.
Displacement of the body at t = 1 s is velocity × time = (1) × (1) m or 1 m.
Velocity of the body at t = 2s is 2 m/s.
Displacement of the body at t = 1 s is velocity × time = (2) × (2) m or 4 m.
Velocity of the body at t = 3 s is 3 m/s.
Displacement of the body at t = 3 s is velocity × time = (3) × (3) m or 9 m
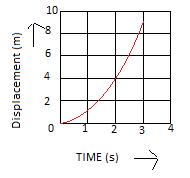
Solution E.9
(i) Distance travelled in any part of the graph can be determined by finding the area enclosed by the graph in that part with the time axis.
(ii) Distance travelled in part BC = Area of the rectangle tBC2t = base × height.
= (2t - t) × vo
= vot
Distance travelled in part AB = Area of the triangle ABt
= (1/2) × base × height
= (1/2) × t × vo
= (1/2) vo t
Therefore, distance travelled in part BC:distance travelled in part AB :: 2:1.
(iii)
(a) BC shows motion with uniform velocity.
(b) AB shows motion with uniform acceleration.
(c) CD shows motion with uniform retardation.
(iv)
(a) The magnitude of acceleration is lower as the slope of line AB is less than that of line CD.
(b) Slope of line AB = vo/t
Slope of line CD = vo/0.5t
Slope of line AB/Slope of line CD = (vo /t)/(vo /0.5t)
Slope of line AB:Slope of line CD :: 1:2.
Solution E.10
(i) Acceleration in the part AB = Slope of AB
= tan (∠BAD)
= (30/4) ms-2
= 7.5 ms-2
Acceleration in the part BC = 0 ms-2
Acceleration in the part CD = slope of CD = -tan (∠CDA)
= -(30/2) ms-2
= -15 ms-2
(ii) Displacement of part AB = Area of ΔAB4 = (1/2) (4) (30)
= 60 m
Displacement of part BC = Area of rectangle 4BC8
= (30) × (4) = 120 m
Displacement of part CD = Area of ΔC8D = (1/2) (2) (30)
= 30 m
(iii) Total displacement = Displacement of part AB + Displacement of part BC + Displacement of part CD
= 60 + 120 + 30 = 210 m
Solution E.11
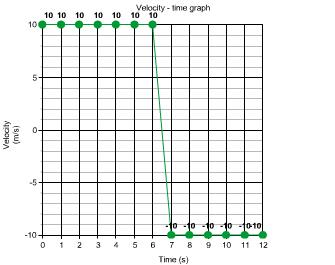
Distance travelled in first 6 s = velocity × time
= 10 m/s × 6
= 60 m/s
Distance travelled in next 6 s = velocity × time
= 10 m/s × 6
= 60 m/s
Total distance travelled in 12 s = (60 + 60) m = 120 m
Total displacement = 0, as the ball returns its starting point.
Solution E.12
(i) From 0 to 4 seconds, the motion is uniformly accelerated and from 4 to 6 seconds, the motion is uniformly retarded.
(ii) Displacement of the particle at 6 s = (1/2) (6) (2) = 6 m
(iii) The particle does not change its direction of motion.
(iv) Distance travelled by the particle from 0 to 4s (D1) = (1/2) (4) (2) = 4 m
Distance travelled by the particle from 4 to 6s (D2) = (1/2) (2) (2) = 2 m
D1:D2:: 4:2
D1:D2:: 2:1
(v) Acceleration from 0 to 4 s = (2/4) ms-2 or 0.5 ms-2
Retardation from 4 s to 6 s = (2/2) ms-2 or 1 ms-2.
Motion in One Dimension Exercise Ex 2(C)
Solution A.1
(d) All of these
Solution A.2
(b) v = at
Solution A.3
(b) Negative
Solution A.4
(b) 2.7 ms-2
A car starts from the rest.
Thus, initial velocity = u = 0m/s
Final velocity = v = 54 m/s
t = 20 s
From first equation of motion,
v = u + at
54 = 0 + a x 20
a = 54/20 = 2.7 m/s2
Solution A.5
(d) 25 m
s = ut + ½ at2
s = 10 x 5 + ½ (-2) x 52
s = 50 - 25 = 25 m
Solution A.6
(a) 5 ms-1
u= 0
a = 0.5 m/s2
s = 25 m
v2 = u2 + 2as
v2 = 0 + 2 × 0.5 × 25 = 25
v = 5 m/s
Solution A.7
(b) 16 m
u = 0
a = 8 m/s2
t = 2 s
s = ut + ½ at2
s = 0 + ½ (8) x 22 = 4 x 4 = 16 m
Solution A.8
(b) 5 km
Given that,
u = 0,
v = 20 km/hr
t = 30 min = 0.5 hr
Now,
v = u + at
20 = 0 + a × 0.5
∴ a = 40 km/h2
Solution B.1
Three equations of a uniformly accelerated motion are
v = u + at
s = ut + (1/2)at2
v2 = u2 + 2as
Solution B.2
Distance = s, time = t, initial velocity u = 0 and acceleration = a.
Using the second equation of motion and substituting the above values we get,
s = ut + (1/2) at2
![]()
Solution C.1
Derivation of equations of motion
First equation of motion:
Consider a particle moving along a straight line with uniform acceleration 'a'. At t = 0, let the particle be at A and u be its initial velocity, and at t = t, let v be its final velocity.

Acceleration = Change in velocity/Time a = (v - u)/t at = v - u v = u+ at ... First equation of motion.
Second equation of motion: Average velocity = Total distance traveled/Total time taken Average velocity = s/t ...(1)
Average velocity can be written as (u+v)/2 Average velocity = (u+v)/2 ...(2)
From equations (1) and (2) s/t = (u+v)/2 ...(3)
The first equation of motion is v = u + at.
Substituting the value of v in equation (3), we get
s/t = (u + u + at)/2 s = (2u + at) t/2 = 2ut + at2/2 = 2ut/2 + at2/2
s = ut + (1/2) at2 …Second equation of motion.
Third equation of motion: The first equation of motion is v = u + at. v - u = at ... (1)
Average velocity = s/t ...(2)
Average velocity =(u+v)/2 ...(3)
From equation (2) and equation (3) we get,
(u + v)/2 = s/t ...(4)
Multiplying eq (1) and eq (4) we get,
(v - u)(v + u) = at × (2s/t) (v - u)(v + u) = 2as
[We make the use of the identity a2 - b2 = (a + b) (a - b)]
v2 - u2 = 2as ...Third equation of motion.
Solution D.1
Initial velocity u = 0
Acceleration a = 2 m/s2
Time t = 2 s
Let 'S' be the distance covered.
Using the second equation of motion,
S = ut + (1/2) at2
S = 0 + (1/2) (2) (2) 2
S = 4 m
Solution D.2
Initial velocity u = 10 m/s
Acceleration a = 5 m/s2
Time t = 5s
Let 'S' be the distance covered.
Using the second equation of motion,
S = ut + (1/2) at2
S = (10)(5) + (1/2) (5) (5) 2
S = 50 + 62.5
S = 112.5 m
Solution D.3
Acceleration = Change in velocity/time taken
In the first two seconds,
Acceleration = [(33.6 - 30)/2] km/h2
= 1.8 km/h2
= 0.5 m/s2 …(i)
In the next two seconds,
Acceleration = [(37.2 - 33.6)/2] km/h2
= 1.8 km/h2
= 0.5 m/s-2…(ii)
From (i) and (ii), we can say that the acceleration is uniform.
Solution D.4
Initial velocity u = 0 m/s
Acceleration a = 2 m/s2
Time t = 5 s
(i) Let 'v' be the final velocity.
Then, (v - u)/5 = 2
v = 10 m/s-1
(ii) Let 's' be the distance travelled.
Using the third equation of motion,
v2 - u2 = 2as
We get,
(10) 2 - (0) 2 = 2(2) (s)
Thus, s = (100/4) m = 25 m
Solution D.5
Initial velocity u = 20 m/s
Final velocity v = 0
Distance travelled s = 10 cm = 0.1 m
Let acceleration be 'a'.
Using the third equation of motion,
v2 - u2 = 2as
We get,
(0) 2 - (20) 2 = 2(a) (0.1)
a = -(400/0.2) m/s2
a = -2000 ms2
Thus, retardation = 2000 ms-2
Solution D.6
Initial velocity u = 20 m/s
Final velocity v = 0
Time taken t = 5 s
Let acceleration be 'a'.
Using the first equation of motion,
v = u + at
0 = 20 + 5a
a = -4 ms-2
Thus, retardation = 4 ms-2
Solution D.7
Let 's' be the distance between stations A and B.
(i) Average speed = Total distance/total time taken
Here, total distance = s + s = 2s
Total time taken = Time taken to travel from A to B + Time taken to travel from B to A.
= [(s/ 60) + (s/ 80)] s
= [ 140 s / 4800] s
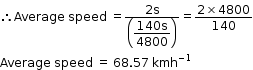
(ii) Average velocity = Displacement/total time taken
Because the train starts and ends at the same station, the displacement is zero. Thus the average velocity is zero.
Solution D.8
Initial velocity u = 90 km/h = 25 m/s
Final velocity v = 0 m/s
Acceleration a = -0.5 m/s2
(i) Let 'V' be the velocity after time t = 10 s
Using the first equation of motion,
v = u + at
We get,
V = 25 + (-0.5) (10) m/s
V = 25 - 5 = 20 ms-1
(ii) Let t' be the time taken by the train to come to rest.
Using the first equation of motion,
v = u + at
We get,
t' = [(0 - 25)/ (-0.5)] s
t' = 50 s
Solution D.9
Distance travelled s = 100 m
Average velocity V = 20 m/s
Final velocity v = 25 m/s
(i) Let u be the initial velocity.
Average velocity = (Initial velocity + Final velocity)/2
V = (u + v)/2
20 = (u + 25)/2
u = 40 - 25 = 15 ms-1
(ii) Let 'a' be the acceleration of the car.
Using the third equation of motion,
v2 - u2 = 2as
We get,
(25) 2 - (15) 2 = 2 (a) (100)
625 - 225 = 200 a
a = (400/200) m/s2 = 2 ms-2
Solution D.10
Final velocity v = 0
Acceleration = -25 cm/s2 or -0.25 m/s2
Time taken t = 20 s
(i) Let 'u' be the initial velocity.
Using the first equation of motion,
v = u + at
We get,
u = v - at
u = 0 - (-0.25)(20) = 5 m/s
(ii) Let 's' be the distance travelled.
Using the third equation of motion,
v2 - u2 = 2as
We get,
(0) 2 - (5)2 = 2 (-0.25) (s)
s = (25/0.5) = 50 m.
Solution D.11
Initial velocity u = 0 m/s
Distance travelled s = 270 m
Time taken to travel s distance = 3 s
Let 'a' be the uniform acceleration.
Using the second equation of motion,
S = ut + (1/2) at2
We get,
270 = 0 + (1/2) a (3)2
270 = 9a/2
a = 60 ms2
Let v be the velocity of the body 10 s after the start.
Using the first equation of motion, we get
v = u + at
v = 0 + (60)(10) = 600 ms-1
Solution D.12
Let the constant acceleration with which the body moves be 'a'.
Given, the body travels distance S1 = 3 m in time t1 = 1 s.
Same body travels distance S2 = 8 m in time t2 = 2 s.
(i) Let 'u' be the initial velocity.
Using the second equation of motion,
S = ut + (1/2) at2
Substituting the value for S1 and S2, we get

(ii) Putting u = 2 m/s in the equation
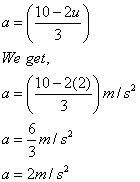
Solution D.13
Initial velocity u = 25 m/s
Final velocity v = 0
(i) Before the brakes are applied, let S be the distance travelled.
Distance = Speed × time
S = (25) × (5) m
S = 125 m
(ii) Acceleration = (Final velocity - Initial velocity)/Time taken
= [(0 - 25)/15] ms-2
= (-5/2) ms-2
= -2.5 ms-2
Therefore, retardation = 2.5 ms-2
(iii) After applying brakes, the time taken to come to stop = 10 s
Let S' be the distance travelled after applying the brakes.
Initial velocity u = 25 m/s
Final velocity v = 0
Using the third equation of motion,
v2 - u2 = 2as
We get,
(0) 2 - (25)2 = 2 (-2.5) (S')
625 = 5(S')
S' = 125 m
Solution D.14
Given, the initial velocity u = 75 km/s
Final velocity v = 120 km/s
Time taken = 6 s
(i) Acceleration = (Final velocity - Initial velocity)/time taken
= [(120 - 75)/6] kms-2
= (45/6) kms-2
= 7.5 kms-2
(ii) Distance travelled by the aircraft in the first 10 s = Distance travelled in the first 6 s + Distance travelled in the next 4 s.
Distance travelled in the first 6s (S1) = ut + (1/2) at2
(S1) = ut + (1/2) at2
(S1) = (75)(6) + (1/2) (7.5)(6)2
(S1) = 450 + 135
(S1) = 585 km
Distance travelled in the next 4 s (S2) = Speed × time
Speed at the end of 6 s is 120 km/s.
(S2) = (120) (4)
(S2) = 480 km
Thus, the distance travelled by the aircraft in the first 10 s = (S1) + (S2) = 585 + 480 = 1065 km.
Solution D.15
(i) For the first 10 s, initial velocity u = 0
Acceleration a = 2 m/s2
Time taken t = 10 s
Let 'v' be the maximum velocity reached.
Using the first equation of motion
v = u + at
We get
V = (0) + (2) (10) = 20 ms-1
(ii) For the last 50 s: Final velocity = 0 m/s, initial velocity = 20 m/s.
Acceleration = (Final velocity - Initial velocity)/time
= (0 - 20)/50 = -0.4 m/s2
Retardation = 0.4 ms-2
(iii) Total distance travelled = Distance travelled in the first 10 s + Distance travelled in 200 s + Distance travelled in last 50 s
Distance travelled in first 10s (s1) = ut + (1/2) at2
S1= (0) + (1/2) (2) (10)2
S1= 100 m
Distance travelled in 200s (s2) = speed × time
S2 = (20) (200) = 4000 m
Distance travelled in last 50s (s3) = ut + (1/2) at2
Here, u = 20 m/s, t = 50 s and a = -0.4 m/s2
S3= (20)(50) + (1/2) (-0.4) (50)2
S3= 1000 - 500
S3= 500 m
Therefore, total distance travelled = S1 + S2 + S3 = 100 + 4000 + 500 = 4600 m
(iv) Average velocity = Total distance travelled/total time taken
= (4600/260) m/s
= 17.69 ms-1
