Class 9 SELINA Solutions Physics Chapter 1: Measurements and Experimentation
Measurements and Experimentation Exercise Ex 1(A)
Solution A.1
(d): All of the above.
To be accepted internationally, a unit must be of convenient size and without ambiguity, reproducible, and its value must not change with place or time.
Solution A.2
(d) Length, mass, time
The following are the three fundamental quantities in mechanics: length, mass, and time.
Solution A.3
(c) 7 fundamental, 2 complementary
There are 7 fundamental units and 2 complementary units in the International System of Units (SI).
i.e.,
The seven fundamental units in the International System of Units (SI) are:
• Meter (m) for length
• Kilogram (kg) for mass
• Second (s) for time
• Ampere (A) for electric current
• Kelvin (K) for temperature
• Mole (mol) for amount of substance
• Candela (cd) for luminous intensity
The two complementary units in the International System of Units (SI) are:
• Radian (rad) for plane angle
• Steradian (Sr) for solid angle
Solution A.4
(d) Second
The seven fundamental units in the International System of Units (SI) are:
• Meter (m) for length
• Kilogram (kg) for mass
• Second (s) for time
• Ampere (A) for electric current
• Kelvin (K) for temperature
• Mole (mol) for amount of substance
• Candela (cd) for luminous intensity
Solution A.5
(b) Litre
The seven fundamental units in the International System of Units (SI) are:
• Meter (m) for length
• Kilogram (kg) for mass
• Second (s) for time
• Ampere (A) for electric current
• Kelvin (K) for temperature
• Mole (mol) for amount of substance
• Candela (cd) for luminous intensity
Solution A.6
(b) One thousandth
One millimetre is one thousandth part of a metre.
i.e, 1 m = 100 cm = 100× 10 mm
or 1 mm = 1/1000 m
Solution A.7
(a) 1.496 × 1011 metre
An astronomical unit (AU) is a length measurement used in astronomy. It is roughly equivalent to the average distance between the Earth and the Sun, which is approximately 1.496× 1011 m.
Solution A.8
(b) Light year
A light year is the distance travelled by light in one year and is a more preferred unit for measuring the distance between stars, particularly those that are very far away.
Solution A.9
(d) 10-15 m
The fermi is the unit of length used to measure small distances in nuclear physics.
i.e., 1 fermi = 10-15m.
Solution A.10
(c) leap year
A leap year is one day longer than a regular year, and it happens every four years to account for the extra quarter day in the solar year.
As a result, the leap year is the only time unit among the following.
Solution A.11
(a) 0.1 nm
1 Å = 10-10 m
and 1 nm = 10-9 m
∴ 1 Å = 10-1 or 0.1 nm
Solution A.12
(a) 10 quintal
The units 'quintal' and 'metric tonne' are two units of mass bigger than 'kilogramme'.
1 quintal = 100 kg
1 metric tonne = 1000 kg
∴ 1 metric tonne = 10 quintal
Solution A.13
(b) Length
A light year is the distance travelled by light in one year and is a more practical unit for measuring the distance between stars, particularly those that are very far away.
Solution A.14
(c) 2 × 1030 kg
The solar mass (M) is a standard unit of mass in astronomy equal to approximately 2×1030 kg and is approximately equal to the mass of the Sun.
The solar mass (M☉) is a standard unit of mass in astronomy equal to about 2×1030 kg and roughly equal to the mass of the Sun.
Solution A.15
(b) 29.5 days
A lunar cycle, also known as a synodic month, is the time it takes for the Moon to return to its original phase (such as full moon to full moon). It takes approximately 29.5 days to complete this cycle.
Solution A.16
(b) 10-8 s
1 Shake = 10 nano-sec
i.e., 1 shake = 10-8 s
Solution A.17
(a) Volt × Ampere
As we know, watt is unit of power.
i.e., Power, P = Voltage (V) × Current (I)
∴ 1 watt = 1 Volt× Ampere.
Solution A.18
(c) Metre3
The seven fundamental units in the International System of Units (SI) are:
• Meter (m) for length
• Kilogram (kg) for mass
• Second (s) for time
• Ampere (A) for electric current
• Kelvin (K) for temperature
• Mole (mol) for amount of substance
• Candela (cd) for luminous intensity
Rest all S.I are derived from these fundamental units hence they are termed as derived unit.
In our case meter3 is a derived unit which is used for measuring volume.
Solution A.19
(a) Joule
Joule is the SI unit of energy, named after the English physicist James Prescott Joule.
Solution A.20
(b) Kg m-1s-2
The pascal (Pa) is the SI unit of pressure, and it is defined as one newton of force per square metre of area. Pressure is defined as force per unit area.
i.e., ![]()
![]()
Solution A.21
(c) Fermi
As we know,
1 Å = 10-10 m
1 mm = 10-3 m
1 fermi = 10-15 m
Hence among the following fermi is the smallest unit.
Solution B.1
Measurement is the process of comparing a given physical quantity with a known standard quantity of the same nature.
Solution B.2
Unit is a quantity of constant magnitude which is used to measure the magnitudes of other quantities of the same manner.
Solution B.3
A physical quantity is expressed as a numerical value followed by a unit.
i.e., Physical quantity = Numerical value × Unit
For example: Force = 10 N
The numerical value denotes the magnitude of the quantity, whereas the unit denotes the type of quantity and the measurement system used.
Solution B.4
Definitions of three fundamental quantities:
S.I. unit of length (m): A metre was originally defined in 1889 as the distance between two marks drawn on a platinum-iridium (an alloy made of 90% platinum and 10% iridium) rod kept at 0°C in the International Bureau of Weights and Measures at serves near Paris.
S.I. unit of mass (kg): In 1889, one kilogramme was defined as the mass of a cylindrical piece of a platinum-iridium alloy kept at International Bureau of Weights and Measures at serves near Paris.
S.I. unit of time (s): A second is defined as 1/86400th part of a mean solar day, i.e.
1s = ![]() × one mean solar day.
× one mean solar day.
Solution B.5
Candela is the SI unit of luminous intensity (cd).
Solution B.6
One parsec is the distance from where the semi-major axis of the orbit of the earth (1 A.U) subtends an angle of one second.
Solution B.7
A fundamental (or basic) unit is that which is independent of any other unit or which can neither be changed nor can be related to any other fundamental unit.
Solution B.8
Derived units are those which depend on the fundamental units, or which can be expressed in terms of the fundamental units.
Solution B.9
A metre was originally defined in 1889 as the distance between two marks drawn on a platinum-iridium (an alloy with 90% platinum and 10% iridium) rod kept at 0o C in the International Bureau of Weights and Measures at serves near Paris.
Solution B.10
1 nm = 10 ![]()
Solution B.11
(a) 1 light year = 9.46 × 1015 m
(b) 1 m = 1010 ![]()
(c) 1 m = 106 µ (micron)
(d) 1 micron = 104 ![]()
(e) 1 fermi = 10-15 m
Solution B.12
(a) 1 g = 10-3 kg
(b) 1 mg = 10-6 kg
(c) 1 quintal = 100 kg
(d) 1 a.m.u (or u) = 1.66 x 10-27 kg
Solution B.13
A leap year is the year in which the month of February has 29 days.
Solution B.14
Yes. Year 2020 is the year divisible by number 4. Hence it is a leap year. Such year has one year extra in the month of February. Hence, the year 2020 have February of 29 days.
Solution B.15
One lunar month is the time in which the moon completes one revolution around the earth. A lunar month is made of nearly 4 weeks.
Solution B.16
(a) 1 nanosecond = 10-9 s
(b) 1 µs = 10-6 s
(c) 1 mean solar day = 86400 s
(d) 1 year = 3.15 × 107 s
Solution B.17
(a) Mass (b) Distance (or length) (c) Time (d) Length
Solution B.18
(a) ms-1 (b) kg ms-2 (c) kg m2s-2 (d) kg m-1s-2
Solution B.19
(a) kg ms-2 (b) kg m2s-3
(c) kg m2s-2 (d) kg m-1s-2
Solution B.20
(a) Area (b) Force (c) Energy
(d) Pressure (f) Power
Solution C.1
The three requirements for selecting a unit of a physical quantity are
(i) It should be possible to define the unit without ambiguity.
(ii) The unit should be reproducible.
(iii) The value of units should not change with space and time.
Solution C.2
Fundamental quantities, units and symbols in S.I. system are
|
Quantity |
Unit |
Symbol |
|
Length |
metre |
m |
|
Mass |
kilogramme |
kg |
|
Time |
second |
s |
|
Temperature |
kelvin |
K |
|
Luminous intensity |
candela |
cd |
|
Electric current |
ampere |
A |
|
Amount of substance |
mole |
mol |
|
Angle |
radian |
rd |
|
Solid angle |
steradian |
st-rd |
Solution C.3
The units of quantities other than those measured in fundamental units can be obtained in terms of the fundamental units, and thus the units so obtained are called derived units.
Example:
Speed = Distance/time
Hence, the unit of speed = fundamental unit of distance/fundamental unit of time
Or, the unit of speed = metre/second or ms-1.
As the unit of speed is derived from the fundamental units of distance and time, it is a derived unit.
Solution C.4
Astronomical unit (A.U.) and kilometer (km) are units of length which are bigger than a metre.
1 km = 1000 m
1 A.U. = 1.496 × 1011 m
Solution C.5
Three convenient units of length and their relation with the S.I. unit of length:
(i) 1 Angstrom (Å) = 10-10 m
(ii) 1 kilometre (km) = 103 m
(iii) 1 light year (ly) = 9.46 × 1015 m
Solution C.6
S.I. unit of mass is 'kilogramme'.
In 1889, one kilogramme was defined as the mass of a cylindrical piece of a platinum-iridium alloy kept at the International Bureau of Weights and Measures at serves near Paris.
Solution C.7
The units 'gramme' (g) and 'milligramme' (mg) are two units of mass smaller than 'kilogramme'.
1 g = 10-3 kg
1 mg = 10-6 kg
Solution C.8
The units 'quintal' and 'metric tonne' are two units of mass bigger than 'kilogramme'.
1 quintal = 100 kg
1 metric tonne = 1000 kg
Solution C.9
The S.I. unit of time is second (s).
A second is defined as 1/86400th part of a mean solar day, i.e.
1 s = ![]() × one mean solar day
× one mean solar day
Solution C.10
The units 'minute' (min) and 'year' (yr) are two units of time bigger than second(s).
1 min = 60 s
1 yr = 3.1536 × 107 s
Solution D.1
Wavelength of light of particular colour = 5800![]()
(a)
(i) 1![]() = 10-1 nm
= 10-1 nm
![]() 5800
5800![]() = 5800 × 10-1 nm
= 5800 × 10-1 nm
= 580 nm
(ii) 1![]() = 10-10 m
= 10-10 m
![]() 5800
5800![]() = 5800 × 10-10 m
= 5800 × 10-10 m
= 5.8 × 10-7 m
(b) The order of its magnitude in metre is 10-6 m because the numerical value of 5.8 is more than 3.2.
Solution D.2
Size of a bacteria = 1 µ
Since 1 µ = 10-6 m
![]() Number of the particle = Total length/size of
Number of the particle = Total length/size of
one bacteria
= 1 m/10-6 m
= 106
Solution D.3
Distance of galaxy = 5.6 × 1025 m
Speed of light = 3 × 108 m/s
(a) Time taken by light = Distance travelled/speed of light
= (5.6 × 1025 / 3 × 108) s
= 1.87 × 1017 s
(b) Order of magnitude = 100 × 1017 s = 1017 s
(This is because the numerical value of 1.87 is less than the numerical value 3.2)
Solution D.4
Wavelength of light = 589 nm
1 Angstrom = 0.1 nm
Thus,
589/0.1 = 5890 ![]()
Solution D.5
Mass of oxygen atom = 16.00 u
1 u = 1.66 × 10-27 kg
Mass of 16 u in kg =16 × 1.66 × 10-27 kg =2.656 × 10-26 kg
Solution D.6
Speed of light = 3 × 108 m/s
Time taken to reach the earth = 8 min = 480 s
Distance = speed × time
= 3 × 108 × 480
= 1440 × 108 m = 1440 × 108 × 10-3 km = 1.44 × 108 km
Solution D.7
'The distance of a star from the earth is 8.33 light minutes.'
This statement means that the light from star takes 8.33 minutes to reach the earth.
1 light minute = 1.8 × 1010 metre
Thus,
8.33 light minutes = 8.33 × 1.8 × 1010 = 1.5 × 1011 m
Measurements and Experimentation Exercise Ex 1(B)
Solution A.1
(b) 1 mm
The least count of an instrument is the smallest measurement which can precisely be taken using that instrument. Thus, for a metre rule least count is 0.1 cm.
Solution A.2
(d) 0.01 cm
The least count of vernier callipers is 0.01 cm
Solution A.3
(b) Depth of a beaker
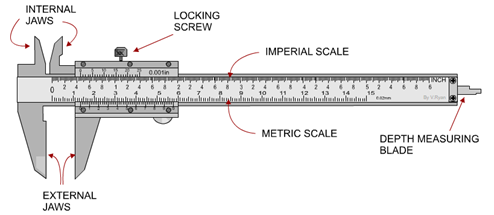
The strip of a vernier calliper is used to measure the depth of a beaker.
The structure of vernier callipers is as shown below.
Solution A.4
(a) +0.06 cm
When the 6th division of the vernier scale coincides with the main scale and the least count is 0.01 cm, the vernier calliper's zero error is +0.06 cm.
Solution A.5
(a) 0.002 cm
L.C of the microscope = L.C of the main scale- L.C of the vernier scale
Now,
L.C of the main scale = 1/20=0.05 cm.
Now, as we know,
24 divisions of the main scale = 25 divisions of the vernier scale
∴ Length of vernier scale = 25/24 =0.96 cm.
L.C of vernier scale= 0.96/20 =0.048 cm
∴ L.C of microscope = 0.05-0.048
L.C of microscope = 0.002 cm.
Solution A.6
(d) To mark circular scale.
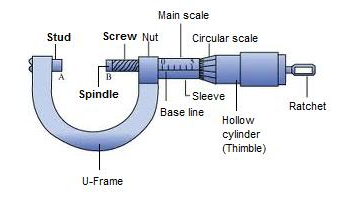
The thimble of a screw gauge is used to mark the circular scale.
Solution A.7
(c) Screw gauge.
Ratchet is a part of a screw gauge.

Solution A.8
(c) a screw gauge
A screw gauge can be used to accurately measure the diameter of a thin wire.
Solution A.9
(a) 0.05 cm
A screw gauge's pitch is the distance moved by the spindle per revolution. In this case, the screw advances 1 mm in two circular head revolutions.
As a result, the pitch is 1 mm / 2 = 0.5 mm = 0.05 cm. As a result, the correct answer is (a) 0.05 cm.
Solution A.10
(a) Metre rule, vernier callipers, screw gauge
The correct ascending order of accuracy is metre rule, vernier callipers, screw gauge.
So, the correct answer is (a) Metre rule, vernier callipers, screw gauge.
Solution B.1
The smallest measurement that an instrument can take accurately is its least count.
For example, if an ammeter has 5 divisions between the marks 0 and 1A, its lowest count is 1/5 = 0.2 A, indicating that it can accurately measure current up to the value 0.2.
Solution B.2
The difference between the values of one main scale division and one vernier scale division is equal to the least number of vernier callipers.
We can increase the resolution of the scale to reduce the least count.
Solution B.3
Vernier constant is equal to the difference between the values of one main scale division and one vernier scale division. It is the least count of vernier callipers.
Solution B.4
A vernier calipers is said to be free from zero error, if the zero mark of the vernier scale coincides with the zero mark of the main scale.
Solution B.5
(a) Outside jaws
(b) Inside jaws
(c) Strip
(d) Outer jaws
Solution B.6
Positive zero error: When the two jaws are brought together, the error is said to be positive if the zero mark of the vernier scale is to the right of the zero mark of the main scale.

Negative zero error: When the two jaws are brought together, the error is said to be negative if the zero mark of the vernier scale is to the left of the zero mark of the main scale.
Solution B.7
A screw gauge's pitch is the distance moved along its axis by the screw in one complete rotation.
Solution B.8
A screw gauge is used for measuring diameter of circular objects mostly wires with an accuracy of 0.001 cm.
Solution B.9
Ratchet helps to advance the screw by turning it until the object is gently held between the stud and spindle of the screw.
Solution B.10
When the anvil and spindle end come into contact due to mechanical errors, the zero mark of the circular scale does not always coincide with the base line of the main scale.
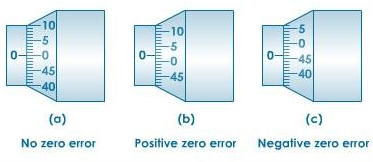
Positive zero error: When the zero mark of the circular scale is lower than the base line of the main scale, the zero error is said to be positive.
Negative zero error: When the zero mark of the circular scale is higher than the base line of the main scale, the zero error is said to be negative.
Solution B.11
(a) Screw gauge
(b) Screw gauge
(c) Vernier calipers
(d) Screw gauge
Solution B.12
Screw gauge measures a length to a high accuracy.
Solution B.13
(a) Vernier callipers (b) Metre scale (c) Screw gauge.
Solution C.1
The least count of an instrument is the smallest measurement that can be taken accurately with it. For example, if an ammeter has 5 divisions between the marks 0 and 1A, then its least count is 1/5 = 0.2 A or it can measure current up to the value 0.2 accurately.
Solution C.2
Total length of the scale = 1 m = 100 cm
No. of divisions = 100
Length of each division = Total length/total no. of divisions
= 100 cm/100
= 1 cm
Thus, this scale can measure with an accuracy of 1 cm.
To increase the accuracy, the total number of divisions on the scale must be increased.
Solution C.3
The least count of a metre rule is 1 cm.
The length cannot be expressed as 2.60 cm because a metre scale measures length correctly only up to one decimal place of a centimeter.
Solution C.4
The least count of vernier callipers is equal to the difference between the values of one main scale division and one vernier scale division.
Let n divisions on vernier callipers be of length equal to that of (n - 1) divisions on the main scale and the value of 1 main scale division be x. Then,
Value of n divisions on vernier = (n - 1) x
Alternatively, value of 1 division on vernier = ![]()
Hence,
Least count = ![]()
L.C. = (Value of one main scale division)/(Total no. of divisions on vernier callipers)
Value of one main scale division = 1 mm
Total no. of divisions on vernier = 10
Therefore, L.C. = ![]()
Solution C.5

Solution C.6
Three uses of vernier callipers are
(a) Measuring the internal diameter of a tube or a cylinder.
(b) Measuring the length of an object.
(c) Measuring the depth of a beaker or a bottle.
Solution C.7
Two scales of vernier calipers are
(a) Main scale
(b) Vernier scale
The main scale is graduated to read up to 1 mm and on vernier scale, the length of 10 divisions is equal to the length of 9 divisions on the main scale.
Value of 1 division on the main scale= 1 mm
Total no. of divisions on the vernier scale = 10
Thus, L.C. = 1 mm /10 = 0.1 mm = 0.01 cm.
Hence, a vernier callipers can measure length correct up to 0.01 cm.
Solution C.8
(i) Pitch: The pitch of a screw gauge is the distance moved by the screw along its axis in one complete rotation.
(ii) Least count (L.C.) of a screw gauge: The L.C. of a screw gauge is the distance moved by it in rotating the circular scale by one division.
Thus, L.C. = Pitch of the screw gauge/total no. of divisions on its circular scale.
If a screw moves by 1 mm in one rotation and it has 100 divisions on its circular scale, then pitch of screw = 1 mm.
Thus, L.C. = 1 mm / 100 = 0.01 mm = 0.001 cm
Solution C.9
The least count of screw gauge can be decreased by -
Increasing the total number of divisions on the circular scale
Reducing the pitch
Solution C.10
Due to mechanical errors, sometimes when the anvil and spindle end are brought in contact, the zero mark of the circular scale does not coincide with the base line of main scale. It is either above or below the base line of the main scale, in which case the screw gauge is said to have a zero error. It can be both positive and negative.
It is accounted by subtracting the zero error (with sign) from the observed reading in order to get the correct reading.
Correct reading = Observed reading - zero error (with sign)
Solution C.11
Diagram of a screw gauge with L.C. 0.001 cm and zero error +0.007 cm.

Solution C.12
Backlash error: If by reversing the direction of rotation of the thimble, the tip of the screw does not start moving in the opposite direction immediately but remains stationary for a part of rotation; it is called backlash error.
Reason: It happens due to wear and tear of the screw threads.
To avoid the backlash error, while taking the measurements the screw should be rotated in one direction only. If the direction of rotation of the screw needs to be changed, then it should be stopped for a while and then rotated in the reverse direction.
Solution D.1
Due to mechanical errors, sometimes the zero mark of the vernier scale does not coincide with the zero mark of the main scale, the vernier callipers is said to have zero error.
It is determined by measuring the distance between the zero mark of the main scale and the zero mark of the vernier scale.
The zero error is of two kinds
(i) Positive zero error
(ii) Negative zero error
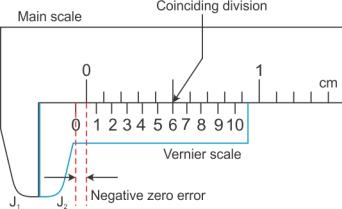
(i) Positive zero error: On bringing the two jaws together, if the zero mark of the vernier scale is on the right of the zero mark of the main scale, the error is said to be positive.
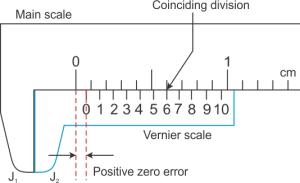
To find this error, we note the division of the vernier scale, which coincides with any division of the main scale. The number of this vernier division when multiplied by the least count of the vernier callipers, gives the zero error.
For example, for the scales shown, the least count is 0.01 cm and the 6th division of the vernier scale coincides with a main scale division.
Zero error = +6 × L.C. = +6 × 0.01 cm
= +0.06 cm
(ii) Negative zero error: On bringing the two jaws together, if the zero mark of the vernier scale is on the left of the zero mark of the main scale, then the error is said to be negative.
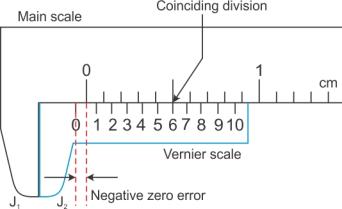
To find this error, we note the division of the vernier scale coinciding with any division of the main scale. The number of this vernier division is subtracted from the total number of divisions on the vernier scale and then the difference is multiplied by the least count.
For example, for the scales shown, the least count is 0.01 cm and the sixth division of the vernier scale coincides with a certain division of the main scale. The total number of divisions on vernier callipers is 10.
Zero error = - (10 - 6) × L.C.
= - 4 × 0.01 cm = - 0.04 cm
Correction:
To get correct measurement with vernier callipers having a zero error, the zero error with its proper sign is always subtracted from the observed reading.
Correct reading = Observed reading - zero error (with sign)
Solution D.2
Diagram of vernier callipers:
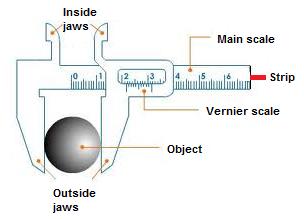
Main parts and their functions:
Main scale: It is used to measure length correct up to 1 mm.
Vernier scale: It helps to measure length correct up to 0.1 mm.
Outside jaws: It helps to measure length of a rod, diameter of a sphere, external diameter of a hollow cylinder.
Inside jaws: It helps to measure the internal diameter of a hollow cylinder or pipe.
Strip: It helps to measure the depth of a beaker or a bottle.
Solution D.3
Measuring the length of a small rod using vernier calipers:
The rod whose length is to be measured is placed in between the fixed end and the vernier scale as shown in the figure.
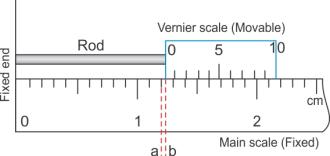
In this position, the zero mark of the vernier scale is ahead of 1.2 cm mark on main scale. Thus the actual length of the rod is 1.2 cm plus the length ab (i.e., the length between the 1.2 cm mark on the main scale and 0 mark on vernier scale).
To measure the length ab, we note the pth division of the vernier scale, which coincides with any division of main scale.
Now, ab + length of p divisions on vernier scale = length of p divisions on main scale
Alternatively, ab = length of p divisions on the main scale - length of p divisions on the vernier scale.
= p (length of 1 division on main scale - length of 1 division on vernier scale)
= p × L.C.
Therefore, total reading = main scale reading + vernier scale reading
= 1.2 cm + (p × L.C.)
Solution D.4
Diagram of screw gauge:
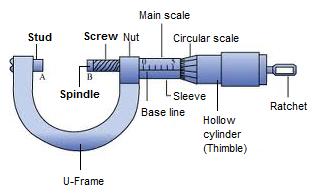
Main parts and their functions:
1. Ratchet: It advances the screw by turning it until the object is gently held between the stud and spindle of screw.
2. Sleeve: It marks the main scale and base line.
3. Thimble: It marks the circular scale.
4. Main scale: It helps to read the length correct up to 1 mm.
5. Circular scale: It helps to read length correct up to 0.01 mm.
Solution D.5
Measurement of diameter of wire with a screw gauge:
The wire whose thickness is to be determined is placed between the anvil and spindle end, the thimble is rotated until the wire is firmly held between the anvil and spindle. The rachet is provided to avoid excessive pressure on the wire. It prevents the spindle from further movement. The thickness of the wire could be determined from the reading as shown in the figure below.

The pitch of the screw = 1 mm
L.C. of screw gauge = 0.01 mm
Main scale reading = 2.5 mm
46th division of circular scale coincides with the base line.
Therefore, circular scale reading = 46 × 0.01 = 0.46 mm
Total reading = Main scale reading + circular scale reading
= (2.5 + 0.46) mm
= 2.96 mm
Solution E.1
Range of the stop watch = 5s
Total number of divisions = 10
L.C. = 5/10 = 0.5 s
Solution E.2
Value of 1 m.s.d. = 1 mm
10 vernier divisions = 9 m.s.d.
L.C. = Value of 1 m.s.d./number of divisions on vernier scale
= 1 mm/10
= 0.1 mm or 0.01 cm
Solution E.3

Thus, the least count of the microscope is 0.001 cm.
Solution E.4
Thickness of the pencil (observed reading) = 1.4 mm
Zero error = + 0.02 cm = + 0.2 mm
Correct reading = observed reading - zero error (with sign)
= 1.4 mm - 0.2 mm
= 1.2 mm
Solution E.5
(i) Value of 1 m.s.d. =1 mm
10 vernier divisions = 9 m.s.d.
L.C. = Value of 1 m.s.d./number of divisions on the vernier scale
= 1 mm/10
= 0.1 mm or 0.01 cm
(ii) On bringing the jaws together, the zero of the vernier scale is ahead of zero of the main scale, the error is positive.
3rd vernier division coincides with a main scale division.
Total no. of vernier divisions = 10
Zero error = +3 × L.C.
= +3 × 0.01 cm
= +0.03 cm
Solution E.6
(i) Value of 1 m.s.d = 1 mm = 0.1 cm
20 vernier divisions = 19 m.s.d.
L.C. = Value of 1 m.s.d./number of divisions on the vernier scale
= 1mm/20
= (0.1/20) cm
= 0.005 cm
(ii) Main scale reading = 35 mm = 3.5 cm
Since 4th division of the main scale coincides with the main scale, i.e. p = 4.
Therefore, the vernier scale reading = 4 × 0.005 cm = 0.02 cm
Total reading = Main scale reading + vernier scale reading
= (3.5 + 0.02) cm
= 3.52 cm
Radius of the cylinder = Diameter (Total reading) / 2
= (3.52/2) cm
= 1.76 cm
Solution E.7
(a) L.C. of vernier callipers = 0.01 cm
Main scale reading = 1.8 cm
Since 4th division of the main scale coincides with the main scale, i.e. p = 4.
Therefore, the vernier scale reading = 4 × 0.01 cm = 0.04 cm
Total reading = Main scale reading + vernier scale reading
= (1.8 + 0.04) cm
= 1.84 cm
(b) Observed reading = 1.84 cm
Zero error = -0.02 cm
Correct reading = Observed reading - Zero error (with sign)
= [1.84 - (-0.02)] cm
= 1.86 cm
Solution E.8
L.C. of vernier callipers = 0.01 cm
In the shown scale,
Main scale reading = 3.3 mm
6th vernier division coincides with an m.s.d.
Therefore, vernier scale reading = 6 × 0.01 cm = 0.06 cm
Total reading = m.s.r. + v.s.r.
= 3.3 + 0.06
= 3.36 cm
Solution E.9
Pitch of a screw gauge = 0.5 mm
No. of divisions on the circular scale = 100
L.C. = (0.5/100) mm
= 0.005 mm or 0.0005 cm
Solution E.10
No. of divisions on the circular scale = 50
(i) Pitch = Distance moved ahead in one revolution
= 1 mm/2 = 0.5 mm
(ii) L.C. = Pitch/No. of divisions on the circular head
= (0.5/50) mm
= 0.01 mm
Solution E.11
Pitch of the screw gauge = 1mm
No. of divisions on the circular scale = 100
(i) L.C. = Pitch/No. of divisions on the circular head
= (1/100) mm
= 0.01 mm or 0.001 cm
(ii) Main scale reading = 2mm = 0.2 cm
No. of division of circular head in line with the base line (p) = 45
Circular scale reading = (p) × L.C.
= 45 x 0.001 cm
= 0.045 cm
Total reading = M.s.r. + circular scale reading
= (0.2 + 0.045) cm
= 0.245 cm
Solution E.12
(i) L.C. of screw gauge = 0.01 mm or 0.001 cm
Main scale reading = 1 mm or 0.1 cm
No. of division of circular head in line with the base line (p) = 27
Circular scale reading = (p) × L.C.
= 27 × 0.001 cm
= 0.027 cm
Diameter (Total reading) = M.s.r. + circular scale reading
= (0.1 + 0.027) cm
= 0.127 cm
(ii) Zero error = 0.005 cm
Correct reading = Observed reading - zero error (with sign)
= [0.127 - (+0.005)] cm
= 0.122 cm
Solution E.13
No. of divisions on the circular scale = 50
(i) Pitch = Distance moved ahead in one revolution
= 1 mm/2 = 0.5 mm
(ii) L.C. = Pitch/No. of divisions on the circular head
= (0.5/50) mm
= 0.01 mm
(iii) Because the zero of the circular scale lies below the base line, when the flat end of the screw is in contact with the stud, the error is positive.
No. of circular division coinciding with m.s.d. = 4
Zero error = + (4 × L.C.)
= + (4 × 0.01) mm
= + 0.04 mm
Solution E.14
No. of divisions on the circular scale = 50
(i) Pitch = Distance moved ahead in one revolution
= 1 mm/1 = 1 mm.
(ii) L.C. = Pitch/No. of divisions on the circular head
= (1/50) mm
= 0.02 mm
(iii) Main scale reading = 4 mm
No. of circular division coinciding with m.s.d. (p) = 47
Circular scale reading = p × L.C.
= (47 × 0.02) mm
= 0.94 mm
Diameter (Total reading) = M.s.r. + circular scale reading
= (4 + 0.94) mm
= 4.94 mm
Solution E.15
Pitch of the screw gauge = 0.5 mm
L.C. of the screw gauge = 0.001 mm
No. of divisions on circular scale = Pitch / L.C.
= 0.5 / 0.001
= 500
Measurements and Experimentation Exercise Ex 1(C)
Solution A.1
(b) Compound pendulum
A compound pendulum is used as the timekeeping element in a pendulum clock.
Solution A.2
(c) Time period
The time period is the amount of time it takes to complete one oscillation. It is timed in seconds (s).
Solution A.3
(c) Frequency
It denotes the number of oscillations performed in one second. Its metric unit is hertz (Hz).
Solution A.4
(c) second
The unit of time period is second.
Solution A.5
(b) f = 1/T
A simple pendulum's time period is inversely proportional to its frequency.
![]()
Solution A.6
(c) Amplitude
The amplitude of oscillation is the maximum displacement of the bob from its mean position on either side.
It is measured in metres (m).
Solution A.7
(c) T2∝ l
As we know that,
![]()
Solution A.8
(b) become twice
Given that,
Mass, m = 1 kg
Initial length = l
Final length, l' = 4l
Now,
![]()
![]()
![]()
![]()
Solution A.9
2 s
Solution A.10
(b)
![]()
As we know,
Time period of simple pendulum is expressed as
![]()
Solution A.11
(a) Length of the pendulum
(a) The time period of oscillations is directly proportional to the square root of the length of the pendulum.
(b) The time period of oscillations of a simple pendulum does not depend on the mass of the bob.
(c) The time period of oscillations of a simple pendulum does not depend on the amplitude of oscillations.
(d) The time period of oscillations of a simple pendulum is inversely proportional to the square root of acceleration due to gravity.
Solution A.12
(b) 1: 4
As we know,
A time period of simple pendulum is expressed as
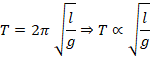
![]()
![]()
Solution A.13
Half
Solution A.14
The time period of a second's pendulum is T = 2 s.
The time period is related to the length as
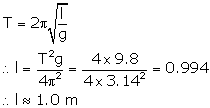
Solution B.1
The maximum displacement of the bob from its mean position on either side is called the amplitude of oscillation. It is measured in metres (m).
Solution B.2
(i) Oscillation: One complete to and fro motion of the pendulum is called one oscillation.
(ii) Amplitude: The maximum displacement of the bob from its mean position on either side is called the amplitude of oscillation. It is measured in metres (m).
(iii) Frequency: It is the number of oscillations made in one second. Its unit is hertz (Hz).
(iv) Time period: This is the time taken to complete once oscillation. It is measured in second(s).
Solution B.3
Two factors on which the time period of a simple pendulum does not depend are
(i) Material of the bob
(ii) Amplitude
Solution B.4
We know that, ![]()
(a) If length quadruples then,
![]()
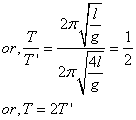
Therefore, the time period is doubled.
(b) If the acceleration due to gravity is reduced to one-fourth,
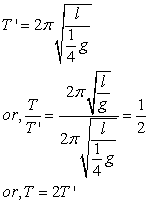
Therefore, the time period is doubled.
Solution B.5
Time period of a simple pendulum is inversely proportional to its frequency.
![]()
Solution B.6
The ratio of their time periods would be 1:1 because the time period does not depend on the weight of the bob.
Solution B.7
A pendulum with the time period of oscillation equal to two seconds is known as a seconds pendulum.
Solution B.8
The frequency of oscillation of a seconds' pendulum is 0.5 s-1. It does not depend on the amplitude of oscillation.
Solution C.1
A simple pendulum is a heavy point mass (known as bob) suspended from a rigid support by a massless and inextensible string.
No, the pendulum used in pendulum clock is not a simple pendulum because the simple pendulum is an ideal case. We cannot have a heavy mass having the size of a point and string having no mass.
Solution C.2
Simple Pendulum:
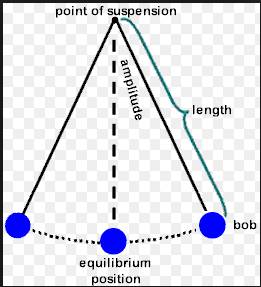
Solution C.3
Two factors on which the time period of a simple pendulum depends are
(i) Length of pendulum (l)
(ii) Acceleration due to gravity (g)
![]()
Solution C.4
Measurement of time period of a simple pendulum:
(i) To measure the time period of a simple pendulum, the bob is slightly displaced from its mean position and is then released. This gives a to and fro motion about the mean position to the pendulum.
(ii) The time 't' for 20 complete oscillations is measured with the help of a stop watch.
(iii)Time period 'T' can be found by dividing 't' by 20.
To find the time period, the time for the number of oscillations more than 1 is noted because the least count of stop watch is either 1 s or 0.5 s. It cannot record the time period in fractions such as 1.2 or 1.4 and so on.
Solution C.5
Pendulum A will take more time (twice) in a given time because the time period of oscillation is directly proportional to the square root of the length of the pendulum. Therefore, the pendulum B will have a greater time period and thus making lesser oscillations.
Solution C.6
(a) The time period of oscillations is directly proportional to the square root of the length of the pendulum.
(b) The time period of oscillations of simple pendulum does not depend on the mass of the bob.
(c) The time period of oscillations of simple pendulum does not depend on the amplitude of oscillations.
(d) The time period of oscillations of simple pendulum is inversely proportional to the square root of acceleration due to gravity.
Solution D.1
The time period of a simple pendulum is directly proportional to the square root of its effective length.
![]()
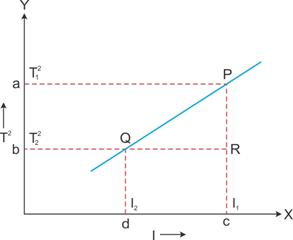
From this graph, the value of acceleration due to gravity (g) can be calculated as follows.
The slope of the straight line can be found by taking two points P and Q on the straight line and drawing normals from these points on the X- and Y-axis, respectively. Then, the value of T2 is to be noted at a and b, the value of l at c and d. Then,
![]()
This slope is found to be constant at a place and is equal to ![]() , where g is the acceleration due to gravity at that place. Thus, g can be determined at a place from these measurements using the following relation:
, where g is the acceleration due to gravity at that place. Thus, g can be determined at a place from these measurements using the following relation:
![]()
Solution E.1
(a) Frequency = Oscillations per second
= (40/60) s-1
= 0.67 s-1
(b) Time period = 1/frequency
= (1/0.67) s
= 1.5 s
Solution E.2
Time period = 2 s
Frequency = 1/time period
= (½)s-1
= 0.5 s-1
Such a pendulum is called the seconds' pendulum.
Solution E.3
Time period of 'a' is inversely proportional to the square root of acceleration due to gravity.
i.e. ![]()
Now, if the acceleration due to gravity falls to one-fourth, the time period will be doubled.
Let the new time period be T' and let g' be the acceleration due to gravity.
Then,
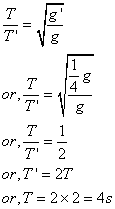
Solution E.4
Given, g= 10 m/s2 and time period (T) = 2s
Let 'l' be the length of the seconds' pendulum.
We know that ![]()

Solution E.5
Let T1 and T2 be the time periods of the two pendulums of lengths 1m and 9m, respectively.

Solution E.6
Time period = Total time/total no. of oscillations
= (5/2) s
= 2.5 s
Let 'l' be the length. Then,

Solution E.7
Let T1 and T2 be the time periods of the two pendulums of lengths l1 and l2, respectively.
Then, we know that the time period is directly proportional to the square root of the length of the pendulum.
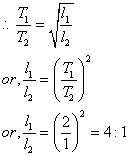
Solution E.8
Time period = Time taken to complete 1 oscillation
= (4 × 0.2) s
= 0.8 s
Solution E.9
Time period of a seconds' pendulum = 2 s
Time taken to complete half oscillation, i.e. from one extreme to the other extreme = 1 s.
