Class 9 SELINA Solutions Maths Chapter 24: Solution of Right Triangles [Simple 2-D Problems Involving One Right-angled Triangle]
Solution of Right Triangles [Simple 2-D Problems Involving One Right-angled Triangle] Exercise Ex. 24
Solution 1(a)
Correct option: (ii) 45o
ABC is an isosceles right-angled triangle.
⇒ AB = BC
⇒ ∠BAC = ∠BCA (angles opposite to equal sides are equal)
Given, ∠ABC = 90o
So, in isosceles right-angled ΔABC,
∠ABC + ∠BAC + ∠BCA = 180o
⇒ 90o + 2∠BAC = 180o
⇒ 2∠BAC = 90o
⇒ ∠BAC = 45o
Solution 1(b)
Correct option: (iii)
![]()
Given, ∠ACB = 90o and ∠CAB = 60o
So, in right-angled ΔACB,
∠ABC + ∠CAB + ∠ACB = 180o
⇒ ∠ABC + 60o + 90o = 180o
⇒ ∠ABC = 30o
Therefore,
cot ∠ABC = cot 30o
= ![]()
Solution 1(c)
Correct option: (iii) 8 m
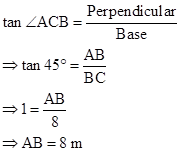
Solution 1(d)
Correct option: (i) 7.32 m

Now,
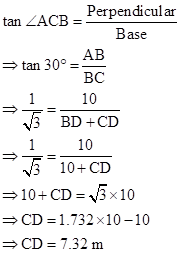
Solution 1(e)
Correct option: (iv) 40 cm
AC = CD (given)
⇒ ∠ADC = ∠DAC (angles opposite to equal sides are equal)
Let ∠ADC = ∠DAC = x
In right-angled ΔABC,
∠ABC + ∠ACB + ∠BAC = 180o
⇒ 90o + 60o + ∠BAC = 180o
⇒ ∠BAC = 30o
In right-angled ΔABD,
∠ABD + ∠BAD + ∠ADB = 180o
⇒ 90o + x + 30o + x = 180o
⇒ 2x = 60o
⇒ x = 30o = ∠ADB
Now,
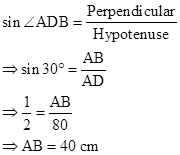
Solution 2
(i)
From the figure we have
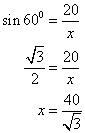
(ii)
From the figure we have
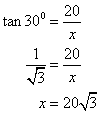
(iii)
From the figure we have
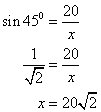
Solution 3
(i)
From the figure we have
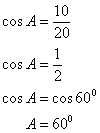
(ii)
From the figure we have

(iii)
From the figure we have

Solution 4
The figure is drawn as follows:
The above figure we have
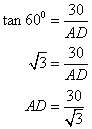
Again
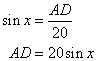
Now
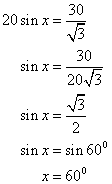
Solution 5
(i)
From the right triangle ABE
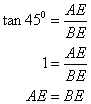
Therefore AE = BE = 50 m.
Now from the rectangle BCDE we have
DE = BC = 10 m.
Therefore the length of AD will be:
AD = AE + DE = 50 + 10 = 60 m.
(ii)
From the triangle ABD we have
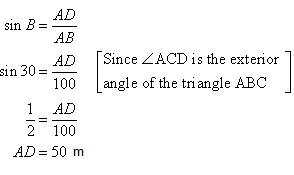
Solution 6

Solution 7
We know, diagonals of a rhombus bisect each other at right angles and also bisect the angle of vertex.
The figure is shown below:
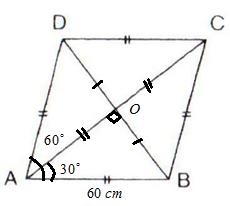
Now
![]()
And ![]()
Also given ![]()
In right triangle AOB
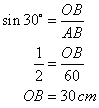
Also
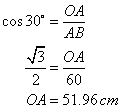
Therefore,
![]() .
.
![]() .
.
Solution 8
Consider the figure
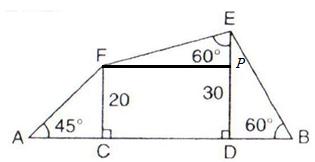
From right triangle ACF
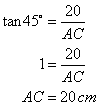
From triangle DEB
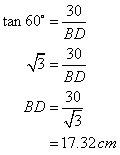
Given ![]() , So
, So ![]()
Therefore
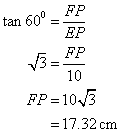
Thus AB = AC + CD + BD = 54.64 cm.
Solution 9
First draw two perpendiculars to AB from the point D and C respectively. Since AB|| CD therefore PMCD will be a rectangle.
Consider the figure,
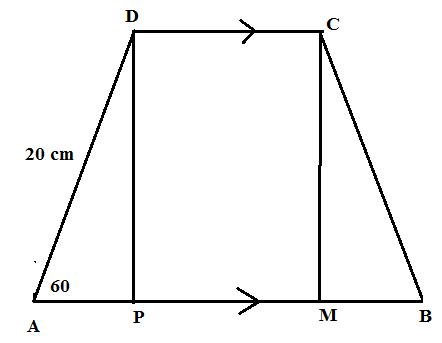
(i)
From right triangle ADP we have
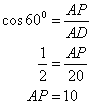
Similarly from the right triangle BMC we have BM = 10 cm.
Now from the rectangle PMCD we have CD = PM = 20 cm.
Therefore
AB = AP + PM + MB = 10 + 20 + 10 = 40 cm.
(ii)
Again from the right triangle APD we have
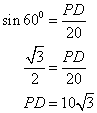
Therefore the distance between AB and CD is ![]() .
.
Solution 10
From right triangle AQP

Also from triangle PBR

Therefore,
AB = AP + PB =![]() .
.
Solution of Right Triangles [Simple 2-D Problems Involving One Right-angled Triangle] Exercise Test Yourself
Solution 1
Solution 2
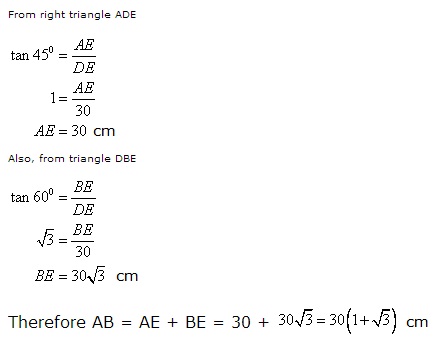
Solution 3
(i)
From the triangle ADC we have
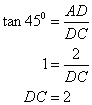
Since AD || DC and![]() , ABCD is a parallelogram and hence opposite sides are equal.
, ABCD is a parallelogram and hence opposite sides are equal.
Therefore AB = DC = 2 cm
(ii)
Again
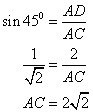
(iii)
From the right triangle ADE we have
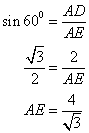
Solution 4
In ∆ABE,

(i) In ∆ABE, m∠AEB = 90°
∴ By Pythagoras Theorem, we get
BE2 = AB2 - AE2
⇒ BE2 = (16)2 - (![]() )2
)2
⇒ BE2 = 256 - 192
⇒ BE2 = 64
⇒ BE = 8cm
(ii) EC = BC - BE = 23 - 8 = 15
In ∆AEC, m∠AEC = 90°
∴ By Pythagoras Theorem, we get
AC2 = AE2 + EC2
⇒ AC2 = (![]() )2 + (15)2
)2 + (15)2
⇒ AC2 = 192 + 225
⇒ AC2 = 147
⇒ AC = 20. 42 cm
Solution 5
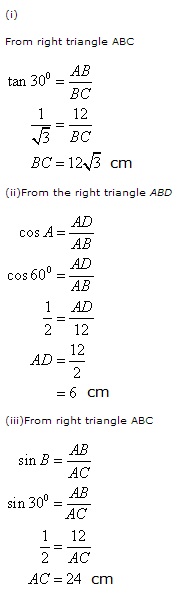
Solution 6
Consider the figure
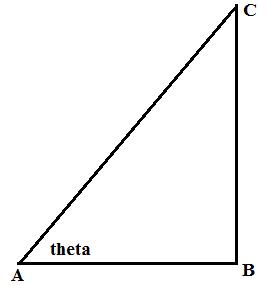
(i) Here AB is ![]() times of BC means
times of BC means

(ii)
Again from the figure
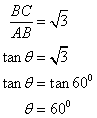
Therefore, magnitude of angle A is 30![]()
Solution 7
Given that the ladder makes an angle of 30o with the ground and reaches upto a height of 15 m of the tower which is shown in the figure below:
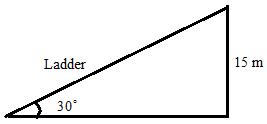
Suppose the length of the ladder is x m
From the figure
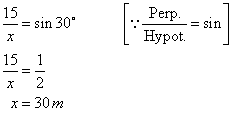
Therefore the length of the ladder is 30m.
Solution 8
Given that the kite is attached to a 100 m long string and it makes an angle of 60![]() with the ground level which is shown in the figure below:
with the ground level which is shown in the figure below:
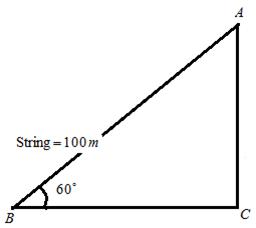
Suppose that the greatest height is x m.
From the figure
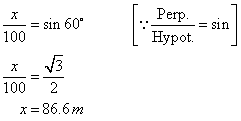
Therefore the greatest height reached by the kite is ![]() .
.
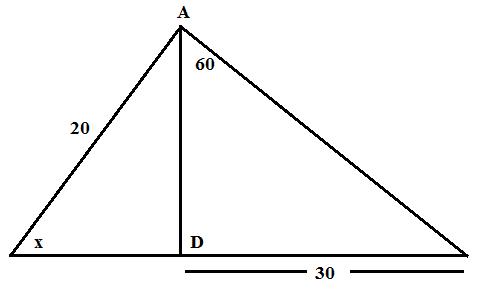
Solution 9
(i)Let BC = xm
BD = BC + CD = (x+20)cm
In ![]() ABD,
ABD,
tan 30![]() =
= ![]()
![]()
x+20 = ![]() AB .....(1)
AB .....(1)
In ![]() ABC
ABC
tan 45![]() =
= ![]()
1 = ![]()
AB = x ... (2)
From (1)
AB + 20 = ![]() AB
AB
AB(![]() -1) = 20
-1) = 20
AB = ![]()
= ![]()
= ![]() = 27.32 cm
= 27.32 cm
From (2)
AB = x = 27.32cm
Therefore BC = x = AB = 27.32cm
Therefore, AB = 27.32cm, BC = 27.32cm
(ii)
Let BC = xm
BD = BC + CD = (x + 20) cm
In ![]() ,
,
tan 30![]() =
= ![]()
![]()
x + 20 = ![]() AB ...(1)
AB ...(1)
In ![]()
tan 60![]() =
= ![]()
![]()
x = ![]() ...(2 )
...(2 )
From (1)
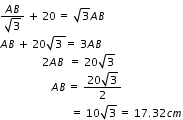
From (2)
![]()
Therefore BC = x = 10cm
Therefore,
AB = 17.32cm, BC = 10cm
(iii)
Let BC = xm
BD = BC + CD = (x + 20)cm
In ![]() ,
,
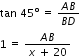
x + 20 = AB ...(1)
In ![]()
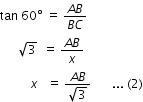
From (1)

From (2)
![]()
![]()
Therefore,
![]()
Solution 10
(i) From ![]()
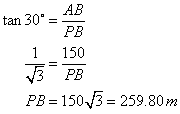
Also, from ![]() ABQ
ABQ
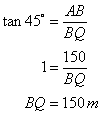
Therefore,

(ii) From ![]()
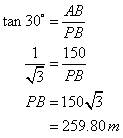
Also, from ![]() ABQ
ABQ
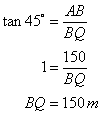
Therefore,
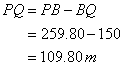
Solution 11
Given tan xo =![]() tan to =
tan to = ![]() and AB = 48 m;
and AB = 48 m;
Let length of BC = xm
From ![]() ADC
ADC

Also, from ![]() BDC
BDC

From (1)

Therefore, length of CD is 45 m.
Solution 12
Since in a rhombus all sides are equal.
The diagram is shown below:
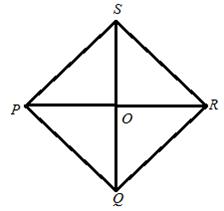
Therefore ![]() ,Let
,Let ![]() .
.
We also know that in rhombus diagonals bisect each other perpendicularly and diagonal bisect the angle at vertex.
Hence POR is a right angle triangle and
Angle OQP = 1/2 (angle PQR) = 1/2 (120) = 60 degrees
![]()
But
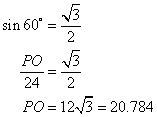
Therefore,
![]()
Also,
![]()
But
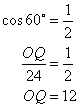
Therefore, ![]()
So, the length of the diagonal ![]() and
and ![]()
