Class 9 SELINA Solutions Maths Chapter 21: Solids [Surface Area and Volume of 3-D Solids]
Solids [Surface Area and Volume of 3-D Solids] Exercise Ex. 21
Solution 1(a)
Correct option: (ii) 4 cm
Let the edge of the cube = 'a' cm
Then, length of the
diagonal![]()
Therefore,
Area of a square on
the diagonal of a cube![]()
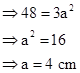
Solution 1(b)
Correct option: (iii) 144 cm2
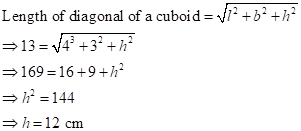
Therefore, volume
of a cuboid = ![]()
= 4 × 3 × 12
= 144 cm3
* Given length, breadth and diagonal of a cuboid, volume of cube cannot be determined.
Solution 1(c)
Correct option: (i) 6 cm
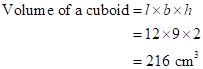
Let the edge of a cube = 'a' cm
Now,
Volume of a cube = Volume of a cuboid
![]()
Solution 1(d)
Correct option: (iv) 18 cm, 12 cm and 12 cm
Let the dimensions of the cuboid be as follows:
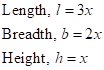
Then,
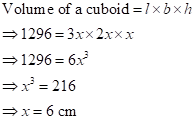
Therefore,
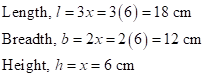
Solution 1(e)
Correct option: (iii) 75 cm
![]()
![]()
Now,
Volume of the soil spread = Area of the field × Rise in level of field
⇒ 960 m3 = 1280 × Rise in level of field
⇒ Rise in level of field = 0.75 m = 75 cm
Solution 1(f)
Correct option: (i) 0.0144 m3
Volume of water flowing in 1 second = 12 × 20 cm3 = 240 cm3
Therefore,
Volume of water flowing in 1 minute = 240 × 60 cm3 = 14,400 cm3 = 0.0144 m3
Solution 1(g)
Correct option: (iv)
![]()
Volume of given solid = Area of cross-section × length
= Area of trapezium × length
![]()
Solution 2
The length, breadth and height of a rectangular solid are in the ratio 5: 4: 2.
Let the length, breadth and height of a cuboid be 5x, 4x and 2x.
Total surface area of a Cuboid = 1216 cm3
⟹ 2(lb + bh + lh) = 1216
⟹ 2(20x2 + 8x2 + 10x2) = 1216
⟹ 76x2 = 1216
⟹ x2 = 16
⟹ x = 4
Therefore, length = 5(4) = 20cm, breadth = 4(4) = 16cm and height = 2(4) = 8cm.
Solution 3
Let a be the one edge of a cube.
Volume![]()
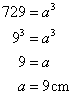
Total surface area=6![]()
Solution 4
Volume of cinema hall![]()
150 ![]() requires= 1 person
requires= 1 person
90000![]() requires=
requires=![]() persons
persons
Therefore, 600 persons can sit in the hall.
Solution 5
Let h be height of the room.
1 person requires 16![]()
75 person requires ![]()
Volume of room is 1200![]()
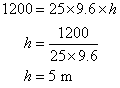
Solution 6
Volume of melted single cube ![]()
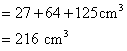
Let a be the edge of the new cube.
Volume![]()
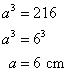
Therefore, 6 cm is the edge of cube.
Solution 7
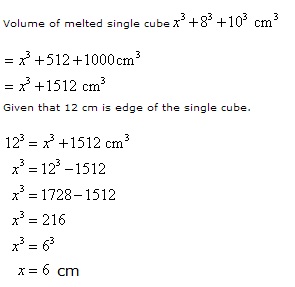
Solution 8
Let the side of a cube be 'a' units.
Total surface area of one cube![]()
Total surface area of 3 cubes ![]()
After joining 3 cubes in a row, length of Cuboid =3a
Breadth and height of cuboid = a
Total surface area of cuboid ![]()
Ratio of total surface area of cuboid to the total surface area of 3 cubes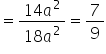
Solution 9

Solution 10
The area of the playground is 3650 m2 and the gravels are 1.2 cm deep. Therefore the total volume to be covered will be:
3650 x 0.012 =43.8 m3.
Since the cost of per cubic meter is Rs. 6.40, therefore the total cost will be:
43.8 x Rs.6.40 = Rs.280.32
Solution 11
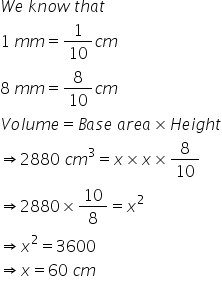
Solution 12
External volume of the box=![]()
Since, external dimensions are 27 cm, 19 cm, 11 cm; thickness of the wood is 1.5 cm.
![]() Internal dimensions
Internal dimensions

Hence, internal volume of box=![]()
(i)
Volume of wood in the box=![]()
(ii)
Cost of wood![]()
![]()
(iii)
Vol. of 4 cm cube=![]()
Number of 4 cm cubes that could be placed into the box
![]()
Solution 13
Area of sheet= Surface area of the tank
![]() Length of the sheet
Length of the sheet![]() its width=Area of 4 walls of the tank +Area of its base
its width=Area of 4 walls of the tank +Area of its base
![]() Length of the sheet
Length of the sheet ![]() 2.5 m=
2.5 m=![]()
![]() Length of the sheet= 300.8 m
Length of the sheet= 300.8 m
Cost of the sheet = 300.8 ![]() Rs 12.50 = Rs 3760
Rs 12.50 = Rs 3760
Solution 14
Let exterior height is h cm. Then interior dimensions are 78-3=75, 19-3=16 and h-3 (subtract two thicknesses of wood). Interior volume = 75 x 16 x (h-3) which must = 15 cu dm
= 15000 cm^3
(1 dm = 10cm, 1 cu dm = 10^3 cm^3).
15000![]() = 75 x 16 x (h-3)
= 75 x 16 x (h-3)
![]() h-3 = 15000/(75x16) = 12.5 cm
h-3 = 15000/(75x16) = 12.5 cm ![]() h = 15.5 cm.
h = 15.5 cm.
Solution 15
(i)
If the side of the cube= a cm
The length of its diagonal= ![]() cm
cm
And,
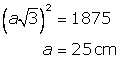
(ii)
Total surface area of the cube=![]()
=![]()
Solution 16
The given figure can be divided into two cuboids of dimensions 6 cm, 4 cm,3 cm, and 9 cm respectively. Hence, volume of solid

Solution 17
Area of cross section of the solid![]()
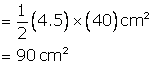
Volume of solid![]()
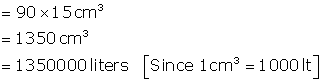
Solution 18
The cross section of a tunnel is of the trapezium shaped ABCD in which ![]() and AM = BN. The height is 2.4 m and its length is 40m.
and AM = BN. The height is 2.4 m and its length is 40m.
(i)
![]()
![]()

Perimeter of the cross- section of the tunnel=![]()
Length=40 m
![]() Internal surface area of the tunnel(except floor)
Internal surface area of the tunnel(except floor)
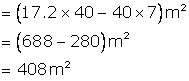
Rate of painting=Rs 5 per![]()
Hence, total cost of painting=Rs 5![]() 408=Rs 2040
408=Rs 2040
(ii)
Area of floor of tunnel![]()
Rate of cost of paving![]()
Total cost=![]()
Solution 19
(i)
The rate of speed ![]()
Volume of water flowing per sec![]()
(ii)
Vol. of water flowing per min![]()
Since 1000![]() = 1 lt
= 1 lt
Therefore, Vol. of water flowing per min=![]()
Solution 20
Vol. of water flowing in 1 sec=![]()
Vol. of water flowing =area of cross section![]() speed of water
speed of water
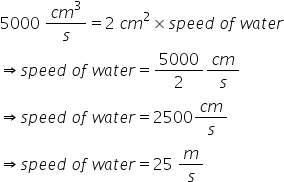
Solution 21
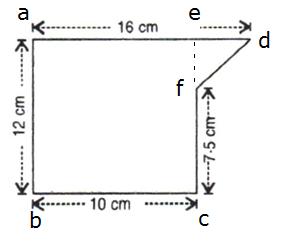
(i)
Area of total cross section= Area of rectangle abce+ area of ![]()
=![]()

(ii)
The volume of the piece of metal in cubic centimeters= Area of total cross section![]()
=![]()
1 cubic centimetre of the metal weighs 6.6 g
![]() of the metal weighs
of the metal weighs![]()
![]()
The weight of the piece of metal to the nearest Kg is 352 Kg.
Solution 22
Vol. of rectangular tank![]()
One liter= 1000![]()
Vol. of water flowing in per sec=
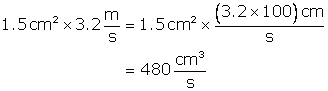
Vol. of water flowing in 1 min=![]()
Hence,
![]() can be filled = 1 min
can be filled = 1 min
![]() can be filled
can be filled![]()
Solids [Surface Area and Volume of 3-D Solids] Exercise Test Yourself
Solution 1
Given that the volume of the iron in the tube 192 cm3
Let the thickness of the tube![]()
![]() Side of the external square=
Side of the external square=![]()
![]() Ext. vol. of the tube
Ext. vol. of the tube ![]() its internal vol.= volume of iron in the tube, we have,
its internal vol.= volume of iron in the tube, we have,

Therefore, thickness is 1 cm.
Solution 2
Let l be the length of the edge of each cube.
The length of the resulting cuboid=![]()
Let width (b) = l cm and its height (h)= l cm
![]() The total surface area of the resulting cuboid
The total surface area of the resulting cuboid
![]()

Therefore, the length of each cube is 6 cm.

Solution 3
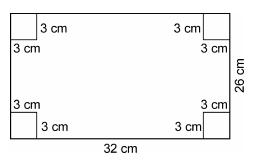
Length of sheet=32 cm
Breadth of sheet=26 cm
Side of each square=3cm
![]() Inner length=32-2
Inner length=32-2![]() 3=32-6=26 cm
3=32-6=26 cm
Inner breadth=![]() cm
cm
By folding the sheet, the length of the container=26 cm
Breadth of the container= 20 cm and height of the container= 3 cm
![]() Vol. of the container=
Vol. of the container=![]()
=![]()
Solution 4
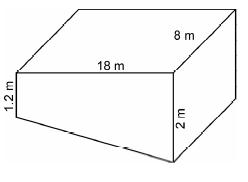
Length of pool= 18 m
Breadth of pool= 8 m
Height of one side= 2m
Height on second side=1.2 m
![]() Volume of pool=
Volume of pool=![]()
Solution 5
Consider the box 1
_SHR_files/20141014183308_image004.jpg)
Thus, the dimensions of box 1 are: 60 cm, 40 cm and 30 cm.
_SHR_files/20141014183308_image006.png)
Consider the box 2
_SHR_files/20141014183308_image008.jpg)
Thus, the dimensions of box 2 are: 40 cm, 30 cm and 30 cm.
_SHR_files/20141014183308_image010.png)
Consider the box 3
_SHR_files/20141014183308_image012.jpg)
Thus, the dimensions of box 2 are: 40 cm, 30 cm and 20 cm.
_SHR_files/20141014183308_image014.png)
_SHR_files/20141014183308_image016.png)
Solution 6
The perimeter of a cube formula is, Perimeter = 4a where (a= length)

Solution 7
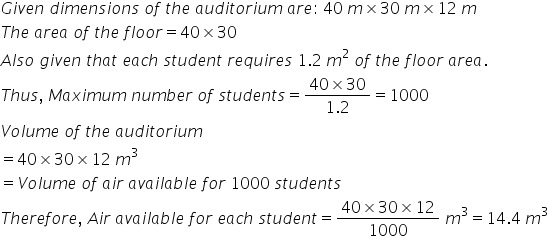
Solution 8
Length of longest rod=Length of the diagonal of the box
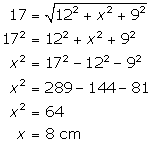
Solution 9
(i)
No. of cube which can be placed along length![]() .
.
No. of cube along the breadth![]()
No. of cubes along the height![]() .
.
![]() The total no. of cubes placed
The total no. of cubes placed![]()
(ii)
Cubes along length![]()
Cubes along width![]() and cubes along height
and cubes along height![]()
![]() The total no. of cubes placed
The total no. of cubes placed![]()
(iii)
Cubes along length![]()
Cubes along width![]() and cubes along height
and cubes along height![]()
![]() The total no. of cubes placed
The total no. of cubes placed![]()
Solution 10
Vol. of the tank= vol. of earth spread

Solution 11
_SHR_files/20141015093546_image002.png)
Solution 12
_SHR_files/20141015093546_image004.png)
_SHR_files/20141015093546_image006.jpg)
_SHR_files/20141015093546_image008.png)
Solution 13
_SHR_files/20141015093546_image016.png)
Solution 14
_SHR_files/20141015093546_image018.png)
Solution 15
_SHR_files/20141015093546_image024.png)
