Class 9 SELINA Solutions Maths Chapter 14 - Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium]
Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium] Exercise Ex. 14(A)
Solution 1(a)
Correct option: (i) 131o
In a polygon of 'n' sides, the sum of the interior angles is equal to (2n - 4) right angles.
Here, n = 7
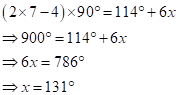
Solution 1(b)
Correct option: (iii) 0o
In a parallelogram, opposite angles are equal.
![]()
Solution 1(c)
Correct option: (ii) 10
In a polygon of 'n' sides, the sum of the interior angles is equal to (2n - 4) right angles.
Here,
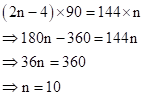
Solution 1(d)
Correct option: (i) 14
Let the number of sides be n.
The sum of the interior angles of the polygon = 6 × the sum of its exterior angles
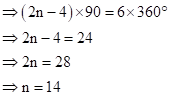
Solution 1(e)
Correct option: (iv) 9
Let the measure of each exterior and interior angle be 2k and 7k.
Let the number of sides in the polygon be n.
Then,
![]()
And,
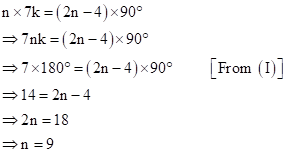
Solution 2
The sum of the interior angle=4 times the sum of the exterior angles.
Therefore the sum of the interior angles = 4×360° =1440°.
Now we have

Thus the number of sides in the polygon is 10.
Solution 3
Let the angles of the pentagon are 4x, 8x, 6x, 4x and 5x.
Thus we can write
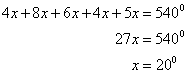
Hence the angles of the pentagon are:
4×20![]() = 80
= 80![]() , 8×20
, 8×20![]() = 160
= 160![]() , 6×20
, 6×20![]() = 120
= 120![]() , 4×20
, 4×20![]() = 80
= 80![]() , 5×20
, 5×20![]() = 100
= 100![]()
Solution 4
Let the measure of each equal angles are x.
Then we can write

Therefore the measure of each equal angles are 116![]()
Solution 5
Let the number of sides of the polygon is n and there are k angles with measure 195o.
Therefore we can write:

In this linear equation n and k must be integer. Therefore to satisfy this equation the minimum value of k must be 6 to get n as integer.
Hence the number of sides are: 5 + 6 = 11.
Solution 6
Let the measure of each equal angles are x.
Then we can write:

Thus the measure of each equal angles are 126o.
Solution 7
Let the measure of each equal sides of the polygon is x.
Then we can write:

Thus the measure of each equal angles are 127o.
Solution 8
Let the measure of the angles are 3x, 4x and 5x.
Thus,

Thus the measure of  = 4×30
= 4×30![]() =120
=120![]()
Solution 9
(i)
Let each angle of measure x degree.
Therefore measure of each angle will be:
![]()
(ii)
Let each angle of measure x degree.
Therefore measure of each exterior angle will be:
![]()
(iii)
Let the number of each sides is n.
Now we can write

Thus the number of sides are 12.
Solution 10
Let measure of each interior and exterior angles are 3k and 2k.
Let number of sides of the polygon is n.
Now we can write:
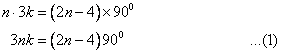
Again
![]()
From (1)

Thus the number of sides of the polygon is 5.
Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium] Exercise Ex. 14(B)
Solution 1(a)
Correct option: (iv) ∠B + ∠C = 180o
In a trapezium, consecutive angles are supplementary.
Therefore, in trapezium ABCD,
∠B + ∠C = 180o
Solution 1(b)
Correct option: (iv) an isosceles right-angled triangle
The diagonals of a square bisect each other at right angle.
Hence, OA = OB and ∠AOB = 90o
Therefore, ΔOAB is an isosceles right-angled triangle.
Solution 1(c)
Correct option: (iii) square
In a square, diagonals are equal and bisect each other at right angles.
Solution 1(d)
Correct option: (iii) opposite angles are bisected by the diagonals
Each diagonal of a parallelogram bisects the parallelogram but opposite angles of a parallelogram are not bisected by the diagonals.
Solution 1(e)
Correct option: (ii) rhombus
A quadrilateral whose diagonals bisect each other at right angle is a rhombus.
Solution 2
(i)True.
This is true, because we know that a rectangle is a parallelogram. So, all the properties of a parallelogram are true for a rectangle. Since the diagonals of a parallelogram bisect each other, the same holds true for a rectangle.
(ii)False
This is not true for any random quadrilateral. Observe the quadrilateral shown below.
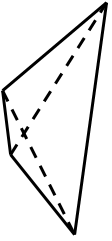
Clearly the diagonals of the given quadrilateral do not bisect each other. However, if the quadrilateral was a special quadrilateral like a parallelogram, this would hold true.
(iii)False
Consider a rectangle as shown below.
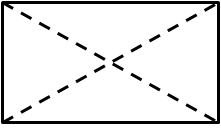
It is a parallelogram. However, the diagonals of a rectangle do not intersect at right angles, even though they bisect each other.
(iv)True
Since a rhombus is a parallelogram, and we know that the diagonals of a parallelogram bisect each other, hence the diagonals of a rhombus too, bisect other.
(v)False
This need not be true, since if the angles of the quadrilateral are not right angles, the quadrilateral would be a rhombus rather than a square.
(vi)True
A parallelogram is a quadrilateral with opposite sides parallel and equal.
Since opposite sides of a rhombus are parallel, and all the sides of the rhombus are equal, a rhombus is a parallelogram.
(vii)False
This is false, since a parallelogram in general does not have all its sides equal. Only opposite sides of a parallelogram are equal. However, a rhombus has all its sides equal. So, every parallelogram cannot be a rhombus, except those parallelograms that have all equal sides.
(viii)False
This is a property of a rhombus. The diagonals of a rhombus need not be equal.
(ix)True
A parallelogram is a quadrilateral with opposite sides parallel and equal.
A rhombus is a quadrilateral with opposite sides parallel, and all sides equal.
If in a parallelogram the adjacent sides are equal, it means all the sides of the parallelogram are equal, thus forming a rhombus.
(x)False
Observe the above figure. The diagonals of the quadrilateral shown above bisect each other at right angles, however the quadrilateral need not be a square, since the angles of the quadrilateral are clearly not right angles.
Solution 3
From the given figure we conclude that
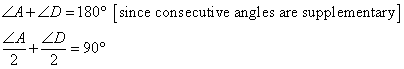
Again from the ![]()
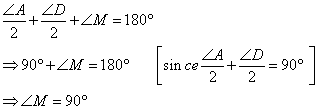
Hence ![]()
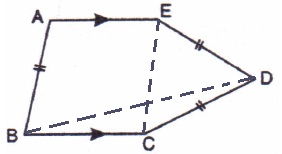
Solution 4
In the given figure

Solution 5
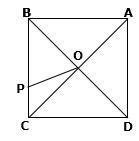

Solution 6
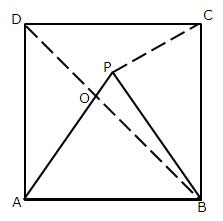
In the given figure ![]() is an equilateral triangle
is an equilateral triangle
Therefore all its angles are ![]()
Again in the
![]()
![]()
Again
![]()
Now
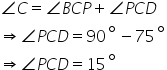
Therefore
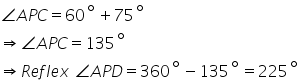
(i)![]()
(ii)![]()
(iii)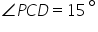
(iv)Reflex 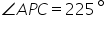
Solution 7
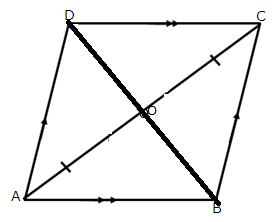
Given that the figure ABCD is a rhombus with angle A = 67o

![text In the rhombus We have end text
angle A equals 67 to the power of degree equals angle C space space space left square bracket text Opposite angles end text right square bracket
angle A plus angle D equals 180 to the power of degree left square bracket text Consecutive angles are supplementary end text right square bracket
rightwards double arrow angle D equals 113 degree
rightwards double arrow angle A B C equals 113 degree
text Consider end text space triangle D B C comma
D C equals C B space left square bracket text Sides of rhombous] end text
S o triangle D B C space text is an isoscales triangle end text
rightwards double arrow angle C D B equals angle C B D
A l s o comma
angle C D B plus angle C D B plus angle B C D equals 180 to the power of degree
rightwards double arrow 2 angle C B D equals 113 to the power of degree
rightwards double arrow angle C D B equals angle C B D equals 56.5 to the power of degree............ left parenthesis i right parenthesis
text Consider end text space triangle D C E comma
E C equals C B
S o triangle D C E space text is an isoscales triangle end text
rightwards double arrow angle C B E equals angle C E B
A l s o comma
angle C B E plus angle C E B plus angle B C E equals 180 to the power of degree
rightwards double arrow 2 angle C B E equals 53 to the power of degree
rightwards double arrow angle C B E equals 26.5 to the power of degree
F r o m space left parenthesis i right parenthesis
angle C B D equals 56.5 to the power of degree
rightwards double arrow angle C B E plus angle D B E equals 56.5 to the power of degree
rightwards double arrow 26.5 to the power of degree plus angle D B E equals 56.5 to the power of degree
rightwards double arrow angle D B E equals 30.5 to the power of degree](https://images.topperlearning.com/topper/tinymce/cache/b8fc555e61bea86f1a043c1939701bc3.png)
Solution 8
(i)ABCD is a parallelogram
Therefore
![]()
Thus

Solving equations (i) and (ii) we have
x=5
y=3
(ii)
In the figure ABCD is a parallelogram
![]()
Therefore
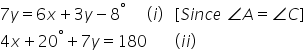
Solving (i), (ii) we have
![]()
Solution 9
Given that the angles of a quadrilateral are in the ratio ![]() Let the angles be
Let the angles be ![]()
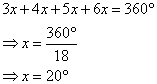
Therefore the angles are
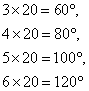
Since all the angles are of different degrees thus forms a trapezium
Solution 10
_SHR_files/20141020191431_image001.jpg)
Given AB = 20 cm and AD = 12 cm.
From the above figure, it's evident that ABF is an isosceles triangle with angle BAF = angle BFA = x
So AB = BF = 20
BF = 20
BC + CF = 20
CF = 20 - 12 = 8 cm
Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium] Exercise Ex. 14(C)
Solution 1(a)
Correct option: (ii) parallelogram
In a parallelogram, both the pairs of opposite sides are equal.
Solution 1(b)
Correct option: (ii) parallelogram
In a parallelogram, both the pairs of opposite angles are equal.
In rectangle and square also, opposite angles are equal and each angle is a right angle.
Solution 1(c)
Correct option: (i) rectangle
If three angles of a quadrilateral are equal to 90o each, then the fourth angle is also 90o as the sum of angles of a quadrilateral is 360o.
Hence, the quadrilateral is a rectangle as each angle of a rectangle is a right angle.
Solution 1(d)
Correct option: (iii) not a parallelogram
In a parallelogram, opposite angles are equal and consecutive angles are supplementary.
Hence, if three angles of a quadrilateral are equal, then the quadrilateral is not a parallelogram.
Solution 1(e)
Correct option: (ii) 30o
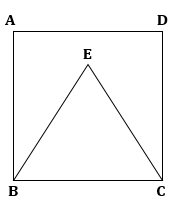
ABCD is a square.
⇒ ∠BCD = 90o
BEC is an equilateral triangle.
⇒ ∠BCE = 60o
Therefore.
∠ECD = ∠BCD - ∠BCE = 90o - 60o = 30o
Solution 2
Let us draw a parallelogram ![]() Where F is the midpoint
Where F is the midpoint
Of side DC of parallelogram ![]()
To prove:![]() is a parallelogram
is a parallelogram
Proof:
Therefore ![]()
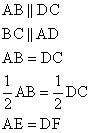
Also AD|| EF
therefore AEFD is a parallelogram.
Solution 3
GIVEN:![]() is a parallelogram where the diagonal
is a parallelogram where the diagonal ![]() bisects
bisects
parallelogram ![]() atangle
atangle ![]()
TO PROVE: ![]() is a rhombus
is a rhombus
Proof : Let us draw a parallelogram ![]() where the diagonal
where the diagonal ![]() bisects the parallelogram at angle
bisects the parallelogram at angle ![]() .
.
Consruction :Let us join AC as a diagonal of the parallelogram
![]()
Since ![]() is a parallelogram
is a parallelogram
Therefore
![]()
Diagonal ![]() bisects angle
bisects angle ![]()
So ![]()
Again ![]() also bisects at
also bisects at ![]()
Therefore ![]()
Thus ![]() is a rhombus.
is a rhombus.
Hence proved
Solution 4

Solution 5
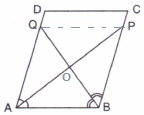
Let us join PQ.
Solution 6
Given ![]() is a parallelogram
is a parallelogram
To prove:![]()
Proof: ![]() is a parallelogram
is a parallelogram
Again,

NOW
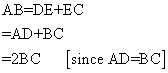
Hence proved
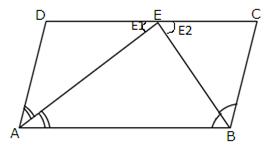
Solution 7
Given ABCD is a parallelogram. The bisectors of ![]() and
and![]() meet at E. The bisectors of
meet at E. The bisectors of ![]() and
and![]() meet at F
meet at F
From the parallelogram ![]() we have
we have
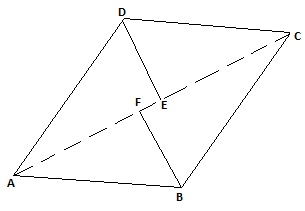

In triangle ECD sum of angles![]()
![]()
Similarly taking triangle ![]() it can be prove that
it can be prove that ![]()
Now since
![]()
Therefore the lines ![]() and BF are parallel
and BF are parallel
Hence proved
Solution 8
Given:![]() is a parallelogram
is a parallelogram

TO PROVE:![]() is a rectangle
is a rectangle
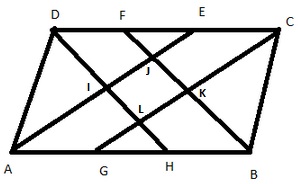
Proof :

![]() is a right triangle because its acute interior angles are complementary.
is a right triangle because its acute interior angles are complementary.
Similarly

since 3 angles of quadrilateral ![]() are right angles,si is the 4th one and so
are right angles,si is the 4th one and so ![]() is a rectangle ,since its interior angles are all right angles
is a rectangle ,since its interior angles are all right angles
Hence proved
Solution 9
Given: Rectangle ABCD in which AZ, BX, CX and DZ are the bisectors of ![]() respectively forming quadrilateral WXYZ.
respectively forming quadrilateral WXYZ.
To prove: Quadrilateral WXYZ is a square.
Proof :
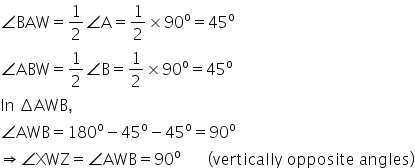
Similarly, it can be proved that 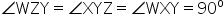 .
.
Hence, quadrilateral WXYZ is a square as each angle is a right angle.
Solution 10
(i)Let![]()
![]()
Also ![]() is the bisector
is the bisector ![]()
![]()
Now ,
![]()
![]()
Therefore ![]()
Now
![]()
Therefore

Also ,![]()
In 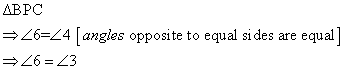
Therefore ![]()
Hence ![]() bisect
bisect ![]()
(ii)
Opposite angles are supplementary
Therefore

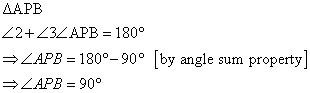
Hence proved
Solution 11
Points ![]() are taken on the diagonal
are taken on the diagonal ![]() of a parallelogram
of a parallelogram ![]() such that
such that ![]() .
.
Prove that ![]() is a parallelogram
is a parallelogram
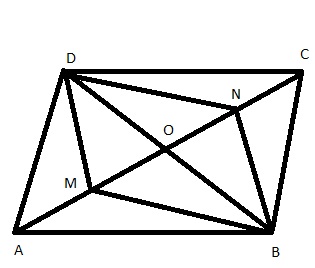
CONSTRUCTION: Join ![]() to meet
to meet ![]() in
in ![]() .
.
PROOF: We know that the diagonals of parallelogram bisect each other.
Now,![]() bisect each other at
bisect each other at ![]() .
.

Thus in a quadrilateral ![]() ,diagonal
,diagonal ![]() are such that
are such that ![]() and
and ![]()
Therefore the diagonals ![]() bisect each other.
bisect each other.
Hence ![]() is a parallelogram
is a parallelogram
Solution 12
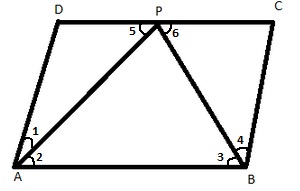
ABCD is a Parallelogram.
Hence opposite sides are parallel and equal.
AD = BC
DC = AB
Also,
DC = AB = 2DP = 2PC.
Now,
DP || AB and AP transversal.
Hence alternate angles are equal
∠DPA = ∠PAB …(1)
Also,
DP || AB and PB transversal.
Hence alternate angles are equal
Hence ∠CPB = ∠PBA … (2)
In ∆ADP
AD = DP
Hence ∆ADP is isosceles.
As a result,
∠DAP = ∠DPA … (3)
Also, in ∆PCB
PC = CB
Hence ∆PCB is isosceles.
As a result,
∠CPB = ∠CBP … (4)
So from (1) and (3),
∠PAB = ∠DAP
Hence AP bisects angle A
And (2) and (4)
∠PBA = ∠CBP
Hence BP bisects angle B
Now in ∆APB, using the angle sum property
∠PAB +∠PBA + ∠APB = 180 …(5)
Also
AD || BC and AB transversal,
Hence interior angles are supplementary
∠DAB + ∠CBA = 180o
Now as AP bisects angle A and BP bisects angle B
2∠DAP + 2∠CBP = 180o … (6)
From (5) and (6)
∠PAB +∠PBA + ∠APB = 2∠DAP + 2∠CBP
Also we have
∠PAB = ∠DAP
∠PBA = ∠CBP
Hence we get
∠DAP + ∠CBP + ∠APB = 2∠DAP + 2∠CBP
∠APB = ∠DAP + ∠CBP
Solution 13
ABCD is a square and ![]()

Solution 14
Given: ![]() is quadrilateral,
is quadrilateral,
![]()
To prove: (i) AC bisects angle BAD.
(ii) AC is perpendicular bisector of BD.
Proof :

Therefore ![]() bisects
bisects ![]()
![]()
![]()
Thus ![]() is perpendicular bisector of
is perpendicular bisector of ![]()
Hence proved
Solution 15
Given ![]() is a trapezium,
is a trapezium,![]()
To prove(i)![]() DAB =
DAB = ![]() CBA
CBA
(ii) ![]() ADC =
ADC = ![]() BCD
BCD
(iii) AC = BD
(iv) OA = OB and OC = OD
Proof :(i) Since ![]() and transversal
and transversal ![]() cuts them at
cuts them at ![]() respectively.
respectively.
Therefore, ![]()
Since ![]()
Therefore ![]() is a parallelogram
is a parallelogram
![]()
![]()
In ![]() ,we have
,we have
Since ![]()
Again ![]()
Hence proved
Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium] Exercise Test Yourself
Solution 1
For (n-1) sided regular polygon:
Let measure of each angle is x.
Therefore
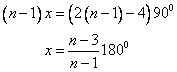
For (n+1) sided regular polygon:
Let measure of each angle is y.
Therefore
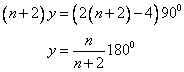
Now we have
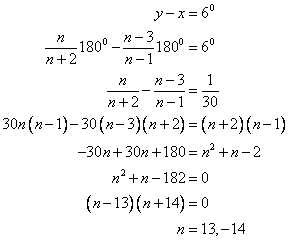
Thus the value of n is 13.
Solution 2
(i)
Let the measure of each exterior angle is x and the number of sides is n.
Therefore we can write:
![]()
Now we have
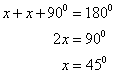
(ii)
Thus the number of sides in the polygon is:
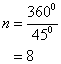
Solution 3
We know that AQCP is a quadrilateral. So sum of all angles must be 360.
∴ x + y + 90 + 90 = 360
x + y = 180
Given x:y = 2:1
So substitute x = 2y
3y = 180
y = 60
x = 120
We know that angle C = angle A = x = 120
Angle D = Angle B = 180 - x = 180 - 120 = 60
Hence, angles of parallelogram are 120, 60, 120 and 60.
Solution 4
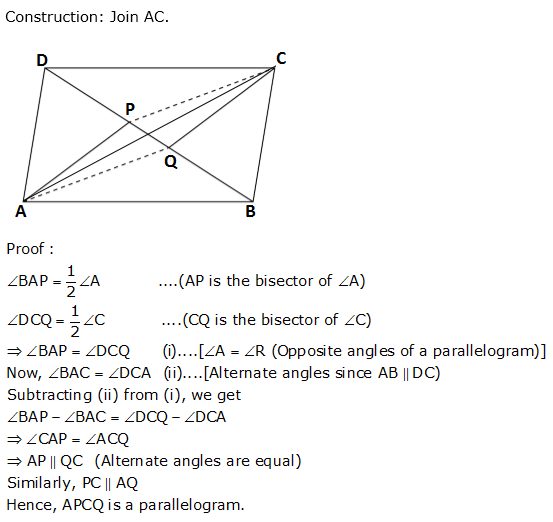
Solution 5
(i)
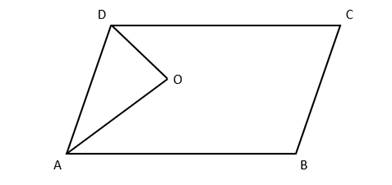
▭ABCD is a parallelogram
Hence CD || AB, also if we consider AD as transversal, we get interior angles supplementary.
Hence,
∠CDA + ∠BAD = 180
Now multiply ½ throughout.
½∠CDA + ½∠BAD = 90 …(1)
Now we have DO and AO as bisectors of ∠CDA and ∠BAD respectively.
Hence,
½∠CDA = ∠ODA
½∠BAD = ∠OAD
So our equation (1) becomes
∠ODA + ∠OAD = 90
Hence, the bisectors of any two adjacent angles intersect at 90o.
(ii)

▭ABCD is a parallelogram
Hence ∠DAB = ∠BCD
Now multiply ½ throughout.
½∠DAB = ½∠DCB …(1)
Now we have AX and CY as bisectors of ∠DAB and ∠DCB respectively.
Hence,
½∠DAB = ∠XAY
½∠BCD = ∠XCY
So our equation (1) becomes
∠XAY = ∠XCY …(2)
Also, XC || YB and YC is transversal, hence alternate angles are equal.
∠XCY = ∠CYB …(3)
From (2) and (3) we have
∠XAY = ∠CYB
Now, these are pair of corresponding angles formed by two lines AX and CY and the transversal AB.
Hence by converse of corresponding angle test, we can say
AX||CY.
Thus, the bisectors of opposite angles are parallel to each other.
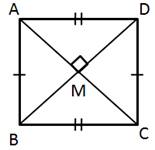
Solution 6

Solution 7

Solution 8
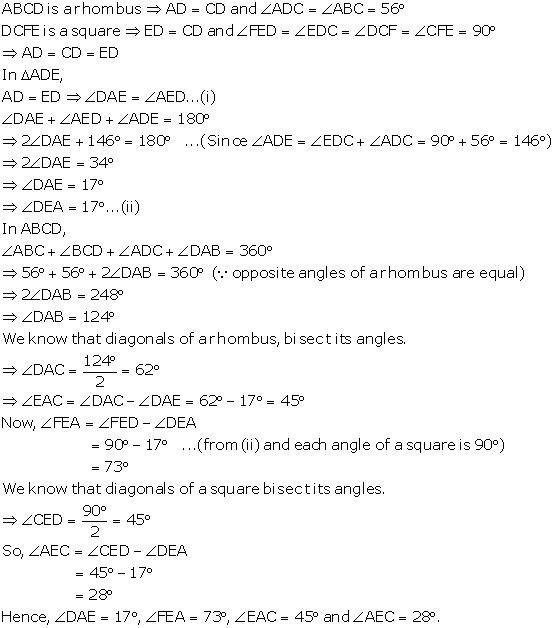
Solution 9(i)
To prove: AE = AD
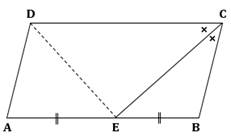
Construction: Join DE
∠DCE = ∠BEC (Alternate angles) (I)
∠DCE = ∠BCE (CE bisects ∠BCD) (II)
From (I) and (II),
∠BEC = ∠BCE
⇒ BC = BE (In a triangle, sides opposite to equal angles are equal)
Also, BC = AD (Opposite sides of a parallelogram)
And, BE = AE (E is the mid-point of AB)
⇒ AE = AD
Solution 9(ii)
To prove: DE bisects angle ADC

Construction: Join DE
AE = AD [From (i)]
∠ADE = ∠AED (In a triangle, angles opposite to equal sides are equal)
∠AED = ∠EDC (Alternate angles)
⇒ ∠ADE = ∠EDC
⇒ DE bisects ∠ADC
Solution 9(iii)
To prove: angle DEC is a right angle

Construction: Join DE
![]() (DE bisects ∠ADC)
(DE bisects ∠ADC)
![]() (CE bisects ∠BCD)
(CE bisects ∠BCD)
Then,
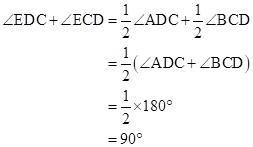
Therefore, in ΔDEC,
Solution 10(i)
To prove: AX = YC
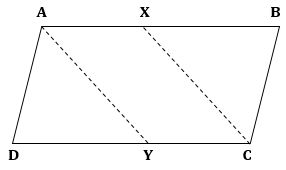
Construction: Join AY and CX
ABCD is a parallelogram.
⇒ AB = CD
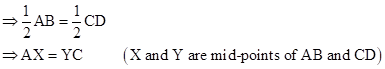
Solution 10(ii)
To prove: AX is parallel to YC

Construction: Join AY and CX
ABCD is a parallelogram.
⇒ AB is parallel to CD
⇒ AX is parallel to YC (X and Y lie on AB and CD respectively)
Solution 10(iii)
To prove: AXCY is a parallelogram

Construction: Join AY and CX
AX = YC [From (i)]
AX is parallel to YC [From (ii)]
Hence, AXCY is a parallelogram as opposite sides are equal and parallel.

