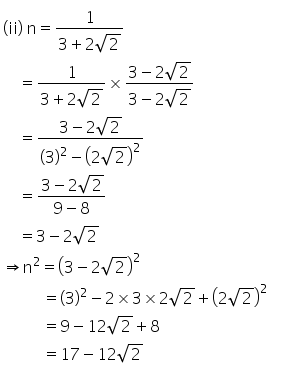Class 9 SELINA Solutions Maths Chapter 1: Rational and Irrational Numbers
Rational and Irrational Numbers Exercise Ex. 1(A)
Solution 1(a)
Correct option: (iii) q ≠ 0
For
a rational number, p and q should be integers and q ≠ 0.
Solution 1(b)
Correct option: (ii) real number
A non-terminating decimal number is a rational number and hence, a real number.
Solution 1(c)
Correct option: (ii) recurring
In 7.478478….., '478' is repeated.
Such a non-terminating decimal, in which a set of digits repeats continuously, is called recurring decimal.
Solution 1(d)
Correct option: (ii) non-terminating
= 0.9466666666……
Hence, it is non-terminating.
Solution 1(e)
Correct option: (iv) None
If the denominator of a rational number can be expressed as 2m × 5n, where m and n are both whole numbers, the rational number is a terminating decimal.
Since, 85 = 5 × 17, 
is
not a terminating decimal.
Since, 405 = 3 × 3 × 3 × 3 × 5, 
is
not a terminating decimal.
Since, 524 = 2 × 2 × 131, 
is
not a terminating decimal.
Hence, none of the given numbers are terminating.
Solution 2
i. False, zero is a whole number but not a natural number.
ii. True, Every
whole can be written in the form of 
, where p and q are integers and q≠0.
iii. True, Every integer can be written in
the form of , where p and q are integers and q≠0.
iv. False.
Example: 
is a rational
number, but not a whole number.
Solution 3
Solution 4
Solution 5(i)
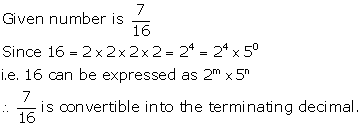
Solution 5(ii)
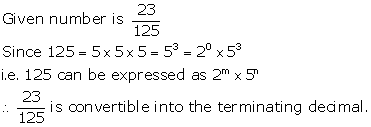
Solution 5(iii)
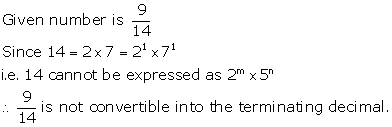
Solution 5(iv)
Solution 5(v)
Rational and Irrational Numbers Exercise Ex. 1(B)
Solution 1(a)
Correct option: (ii) an irrational number
Negative of an irrational number is an irrational number.
For example, 
is
an irrational number indicates - is also an irrational
number.
Solution 1(b)
Correct option: (ii) irrational
which
is irrational.
Solution 1(c)
Correct option: (i)
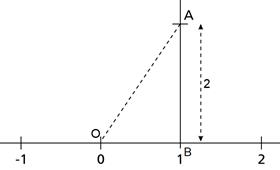
In right-angled DABO,
OA2 = AB2 + OB2 = 22 + 12 = 4 + 1 = 5
⇒
OA =
Solution 1(d)
Correct option: (ii)
, which is irrational.
Solution 1(e)
Correct option: (i)
Since 
are
irrational numbers between 8 and 11.
Hence, 
and 
are two irrational numbers between 8 and 11.
Solution 2
(i) 
Irrational
(ii) 
Irrational
(iii) 
Rational
(iv) 
Irrational
Solution 3
(i)
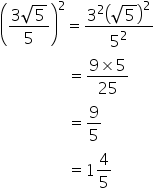
(ii)
(iii)
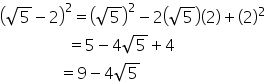
(iv)
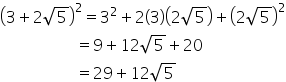
Solution 4
(i) False
(ii) 
which is true
(iii) 
True.
(iv) False because
which is recurring and non-terminating and hence it is rational
(v) True because 
which is recurring and non-terminating
(vi) True
(vii) False
(viii) True.
Solution 5
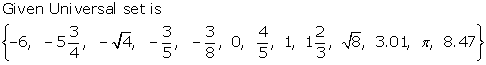
(i)
(ii)
(iii)
(iv)
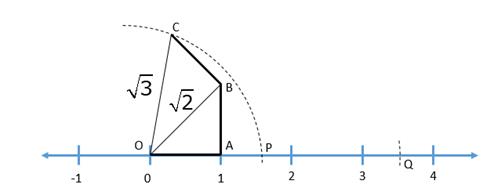
Solution 6
1. Take OA = 1 unit and draw ∠OAB = 90o such that AB = 1 unit. Hence by Pythagoras, OB =
2. Now draw ∠OBC = 90o such that BC = 1 unit. Hence by Pythagoras, OC =
3. With point O as center and OC as radius, draw an arc which meets the number line at point P, so OP =
4. Now with P as center and OP as radius, draw an arc which meets the number line at point Q, so OQ = 2
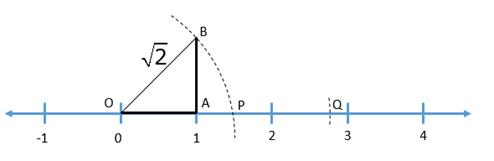
1. Take OA = 1 unit and draw ∠OAB = 90o such that AB = 1 unit. Hence by Pythagoras, OB =
2. Now with point O as center and OB as radius, draw an arc which meets the number line at point P, so OP =
3. Now with P as center and OP as radius, draw an arc which meets the number line at point Q, so OQ = 2
1. Draw the figure as shown below
2. Clearly, O'P = O'O + OP =
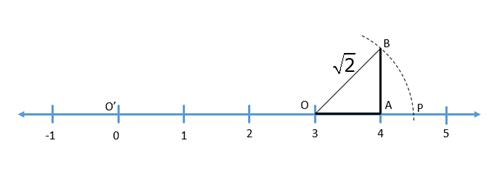
1. Draw the figure as shown below
2. Clearly, O'P' = O'O - OP' =
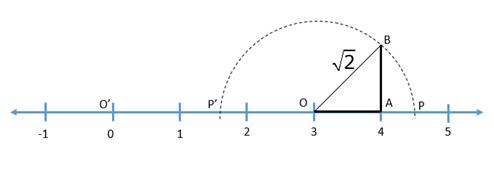
1. Take OA = 2 units and draw ∠OAB = 90o such that AB = 1 unit. Hence by Pythagoras OB =
2. With point O as center and OB as radius, draw an arc which meets the number line at point P, so OP =
3. Now with P as center and OP as radius, draw an arc which meets the number line at point Q, so OQ = 2
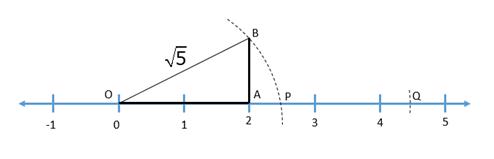
Solution 7
Let 
be a rational number.
⇒ = x
Squaring on both the sides, we get
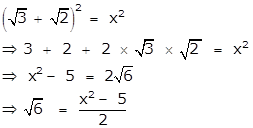
Here, x is a rational number.
⇒ x2 is a rational number.
⇒ x2 - 5 is a rational number.
⇒ 
is also a rational number.
is a rational number.
But 
is an irrational number.
is an irrational number.
⇒ x2- 5 is an irrational number.
⇒ x2 is an irrational number.
⇒ x is an irrational number.
But we have assume that x is a rational number.
∴ we arrive at a contradiction.
So, our assumption that is a rational number is wrong.
∴ is an irrational number.
Let 
be a rational number.
⇒ = x
Squaring on both the sides, we get
Here, x is a rational number.
⇒ x2 is a rational number.
⇒ 11 - x2 is a rational number.
⇒ 
is also a rational number.
is a rational number.
But 
is an irrational number.
is an irrational number.
⇒ 11 - x2 is an irrational number.
⇒ x2 is an irrational number.
⇒ x is an irrational number.
But we have assume that x is a rational number.
∴ we arrive at a contradiction.
So, our assumption that 
is a rational number is wrong.
∴ is an irrational number.
Let 
be a rational number.
⇒ = x
Squaring on both the sides, we get
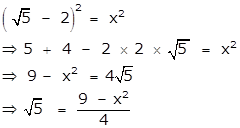
Here, x is a rational number.
⇒ x2 is a rational number.
⇒ 9 - x2 is a rational number.
⇒ 
is also a rational number.
is a rational number.
But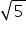 
is an irrational number.
is an irrational number.
⇒ 9 - x2 is an irrational number.
⇒ x2 is an irrational number.
⇒ x is an irrational number.
But we have assume that x is a rational number.
∴ we arrive at a contradiction.
So, our assumption that 
is a rational number is wrong.
∴ is an irrational number.
Solution 8
are irrational numbers whose sum is irrational.
which is irrational.
Solution 9
and 
are two irrational numbers whose sum is rational.
Solution 10
and 
are two irrational numbers whose difference is irrational.
which is irrational.
Solution 11
and 
are irrational numbers whose difference is rational.
which is rational.
Solution 12
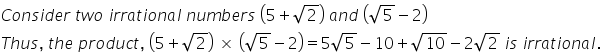
Solution 13
Solution 14
(i) 
and 45 < 48 
(ii) 
and40 < 54 
(iii) 
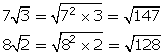
and 128 < 147 < 180
Solution 15
(i) 
Since 162 > 96
(ii) 
141 > 63 
Solution 16
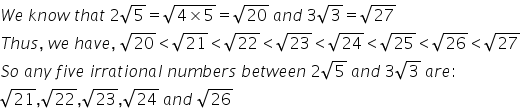
Solution 17
We want rational numbers a/b and c/d such that: 
< a/b < c/d < 
Consider any two rational numbers between 2 and 3 such that they are perfect squares.
Let us take 2.25 and 2.56 as 
Thus we have,
Solution 18
Consider some rational numbers between 3 and 5 such that they are perfect squares.
Let us take, 3.24, 3.61, 4, 4.41 and 4.84 as
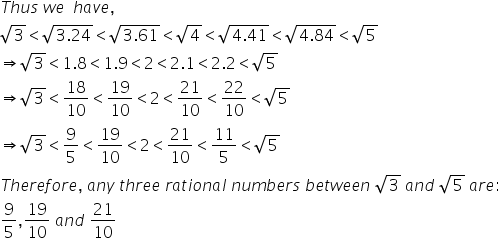
Rational and Irrational Numbers Exercise Ex. 1(C)
Solution 1(h)
Correct option:
(iv) 
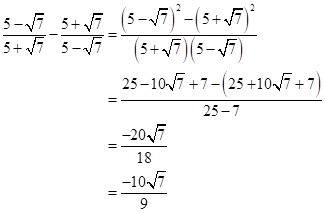
Solution 1(g)
Correct option: (iii) 4
Rationalising,
Solution 1(f)
Correct option:
(ii) 
Solution 1(e)
Correct option: (i)
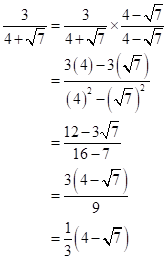
Solution 1(d)
Correct option: (iv)
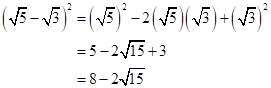
Solution 1(c)
Correct option: (iii) 3
Solution 1(b)
Correct Option:
Rationalising,
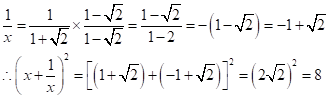
Solution 1(a)
Correct option: (i)
Rationalising,
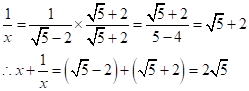
Solution 2
(i) 
Which is irrational
is a surd
(ii) 
Which is irrational
is a surd
(iii) 
is a surd
(iv) 
which is rational
is not a surd
(v) 
is not a surd
(vi) 
= -5
is is not a surd
(vii) 
not a surd as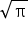 
is irrational
(viii) 
is not a surd because 
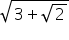is irrational.
Solution 3
(i) 
which is rational
lowest rationalizing factor is 
(ii) 
lowest rationalizing factor is 
(iii) 
lowest rationalizing factor is 
(iv) 
Therefore, lowest rationalizing factor is 
(v) 
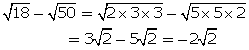
lowest rationalizing factor is
(vi) 
Therefore lowest rationalizing factor is 
(vii) 
Its lowest rationalizing factor is 
Solution 4
(i)
(ii)
(iii)
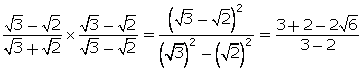
(iv)
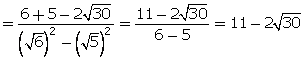
(v)
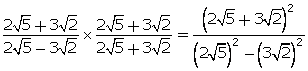
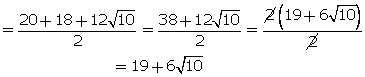
Solution 5
(i) 
(ii) 
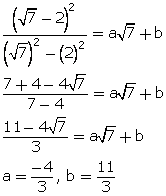
(iii) 
Solution 6
(i)
(ii)
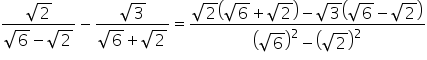
Solution 7
(i)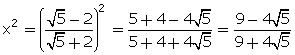 
(ii)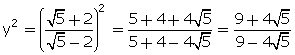 
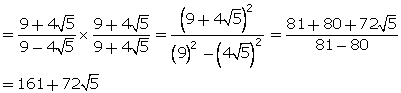
(iii) xy =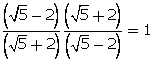 
(iv) x2 + y2 + xy = 161 - 
= 322 + 1 = 323
Solution 8
Solution 9
(i) 
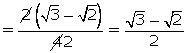
(ii) 
(iii) 
Solution 10
Solution 11
Solution 12
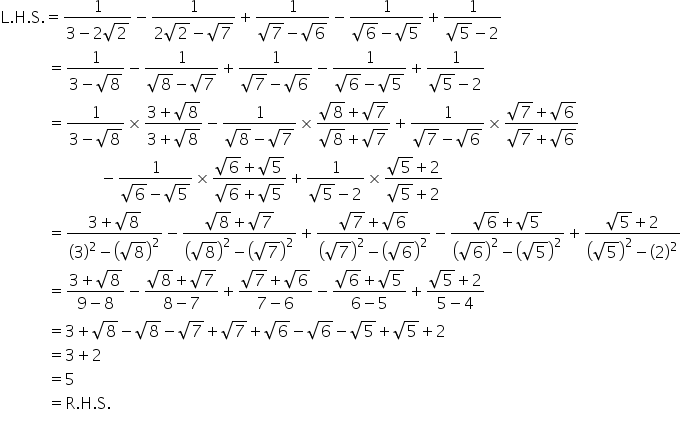
Solution 13
Solution 14(i)
Solution 14(ii)
Solution 14(iii)
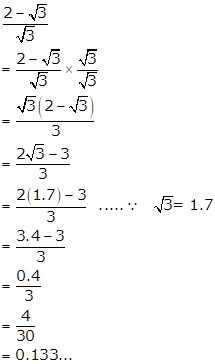
Solution 15
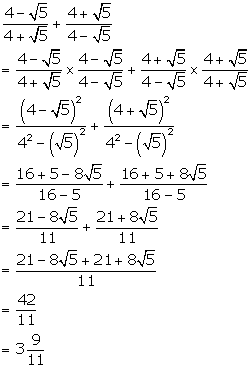
Solution 16
Rational and Irrational Numbers Exercise Test Yourself
Solution 1
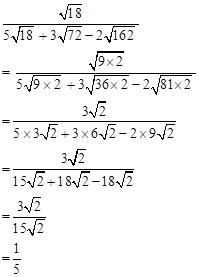
Solution 2
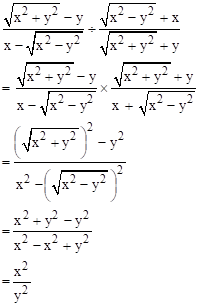
Solution 3
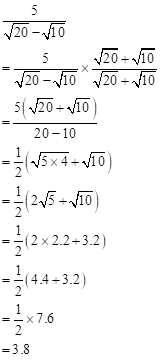
Solution 4
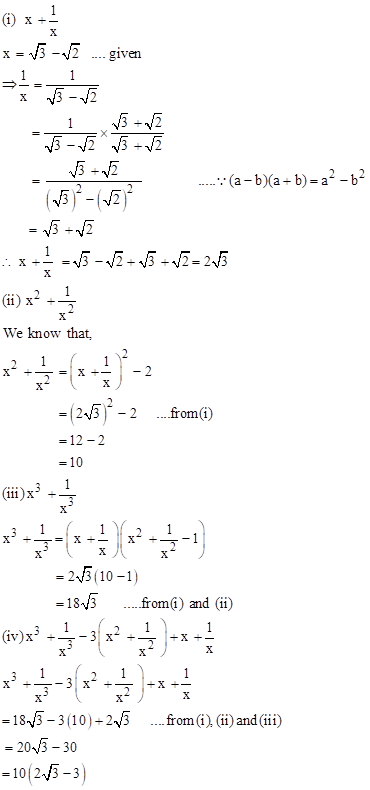
Solution 5
Proof:
(i)
The given statement is TRUE.
Let us assume that negative of an irrational number is a rational number.
Let p be an irrational number,
→ - p is a rational number.
→ - (-p) = p is a rational number.
But p is an irrational number.
Therefore our assumption was wrong.
So, Negative of an irrational number is irrational number.
(ii)
The given statement is FALSE.
We know that 3 is a non - zero rational number and 
is an irrational number.
So, 3 ×= 3 is an irrational.
Therefore, the product of a non - zero rational number and an irrational number is an irrational number.
Solution 6
Since 
So, first we need to find 
and mark it on number line and then find 
Steps to draw 
on the number line are:
- Draw a number line and mark point O.
- Mark point A on it such that OA = 1 unit.
- Draw right triangle OAB such that ∠A = 90° and AB = 1 unit.
- Join OB.
- By Pythagoras Theorem,
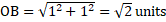. - Draw a line BC perpendicular to OB such that BC = 1.
- Join OC. Thus, OBC is a right triangle. Again by Pythagoras Theorem, we have
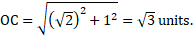
- With centre as O and radius OC draw a circle which meets the number line at a point E.
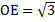units. Thus, OE represents 
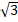on the number line.
Solution 7
Since, 
We need to construct a right - angled triangle OAB, in which
∠A = 90°, OA = 2 units and AB = 2 units.
By Pythagoras theorem, we get
OB2 = OA2 + AB2
∴ OB = 
units
STEPS:
- Draw a number line.
- Mark point A on it which is two points (units) from an initial point say O in the right/positive direction.
- Now, draw a line AB = 2 units which is perpendicular to A.
- Join OB to represent the hypotenuse of a triangle OAB, right angled at A.
- This hypotenuse of triangle OAB is showing a length of OB.
- With centre as O and radius as OB, draw an arc on the number line which cuts it at the point C.
- Here, C represents
.
Solution 8
Solution 9
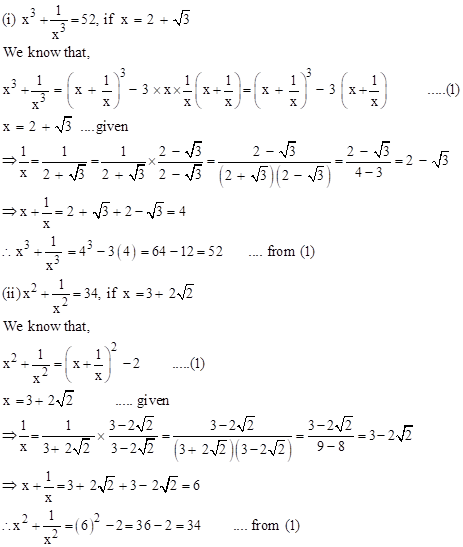
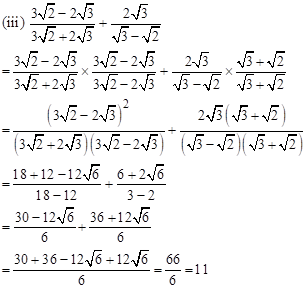
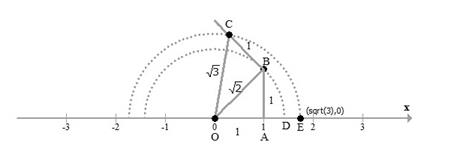
Solution 10
(i) x2 = 6
(ii) x2 = 0.009
(iii) x2 = 27
Solution 11
(i) x2 = 16
Taking square root on both the sides, we get
x = ± 4
As we know that 4 = 
and -4 =
are rational numbers.
⇒ x is rational , if: x2 = 16 .
(ii) x2 = 0.0004 (iii) x2 = 
x2 = 0.0004 = 
Taking square root on both the sides, we get
…. is a rational number.
⇒ x is rational , if: x2 =0.0004.
(iii) x2 =
Taking square root on both the sides, we get
…. is a rational number.
⇒ x is rational , if: x2 =.
Solution 12
From the image, it is cleared that
AB = x, BC = 1
⇒ AC = AB + BC = x + 1
O is a centre of the semi - circle with AC as diameter.
OA, OC and OD are the radii.
⇒ OA = OC = OD = 
OB = OC - BC = 
m∠OBD = 90° … given in the image
∴By Pythagoras theorem, we get
OD2 = OB2 + BD2
⇒ BD2 = OD2 - OB2
⇒
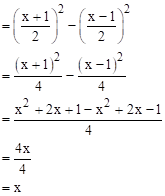