Class 9 SELINA Solutions Maths Chapter 13: Pythagoras Theorem [Proof and Simple Applications with Converse]
Pythagoras Theorem [Proof and Simple Applications with Converse] Exercise Ex. 13(A)
Solution 1(a)
Correct option: (iii) right-angled triangle
Let the three sides of a triangle be 5x, 12x and 13x respectively.
Now,
(5x)2 + (12x)2 = 25x2 + 144x2 = 169x2 = (13x)2
Since, the sum of the squares of two sides is equal to the square of the largest side, the given triangle is the right-angled triangle.
Solution 1(b)
Correct option: (ii) 8 cm and 6 cm
In right-angled triangle
Hypotenuse = 10 cm
Let the other two sides be 3x and 4x respectively.
Now,
(3x)2 + (4x)2 = (10)2
⇒ 9x2 + 16x2 = 100
⇒ 25x2 = 100
⇒ x2 = 4
⇒ x = 2
Therefore,
3x = 3(2) = 6 cm
4x = 4(2) = 8 cm
Solution 1(c)
Correct option: (i) ![]()
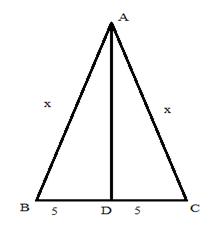
Construction: Draw median AD.
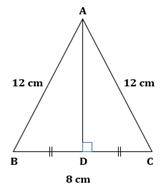
BD = CD (AD is the median)
Now, median of an isosceles triangle is also perpendicular to the base.
∴ AD ⊥ BC
In right-angled ΔADC,
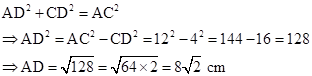
Therefore,
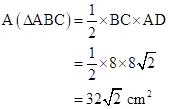
Solution 1(d)
Correct option: (iv) 100 cm

ABCD is a rhombus.
Diagonal AC = 40 cm
Diagonal BD = 30 cm
Now, all sides of a rhombus are equal and diagonals of a rhombus bisect each other at right angles.
So, in right-angled triangle AOB,
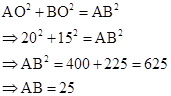
Therefore, the perimeter of rhombus ABCD
= AB + BC + CD + AD
= (25 + 25 + 25 + 25) cm
= 100 cm
Solution 1(e)
Correct option: (i) 4 cm
In right-angled triangle BCD,

In right-angled triangle ABD,
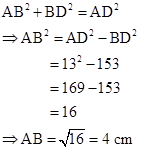
Solution 2
The pictorial representation of the given problem is given below,
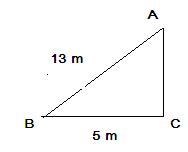
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
(i)Here, AB is the hypotenuse. Therefore applying the Pythagoras theorem we get,
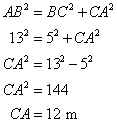
Therefore, the distance of the other end of the ladder from the ground is 12m
Solution 3
Here , we need to measure the distance AB as shown in the figure below,
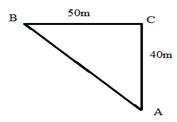
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Therefore , in this case
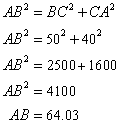
Therefore the required distance is 64.03 m.
Solution 4
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
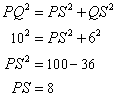
Now, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
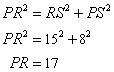
The length of PR![]()
Solution 5
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,

Now, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,

The length of AB is 4 cm.
Solution 6
Since ABC is an equilateral triangle therefore, all the sides of the triangle are of same measure and the perpendicular AD will divide BC in two equal parts.
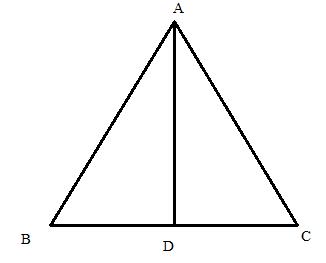
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Here, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
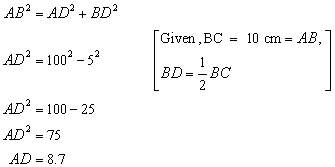
Therefore, the length of AD is 8.7 cm
Solution 7
We have Pythagoras theorem which states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
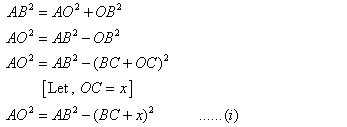
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
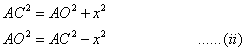
Now, from (i) and(ii),
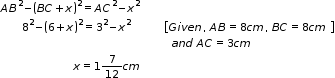
![]()
Solution 8
Here, the diagram will be,
We have Pythagoras theorem which states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Since, ABC is an isosceles triangle, therefore perpendicular from vertex will cut the base in two equal segments.
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
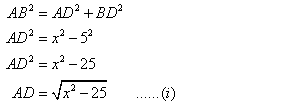

Therefore, x is 13cm
Solution 9
Let, the sides of the triangle be, ![]()
Now, ![]()
Here, in (i) it is shown that, square of one side of the given triangle is equal to the addition of square of other two sides. This is nothing but Pythagoras theorem which states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Therefore, the given triangle is a right angled triangle.
Solution 10
The diagram of the given problem is given below,
We have Pythagoras theorem which states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.

Pythagoras Theorem [Proof and Simple Applications with Converse] Exercise Ex. 13(B)
Solution 1(a)
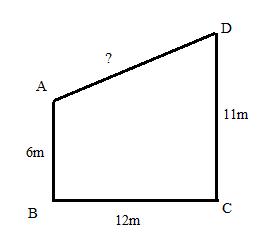
Correct option: (ii) 2AC2
In right-angled triangle ACB,
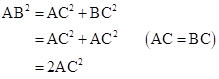

Solution 1(b)
Correct option: (ii) AB2 + DE2
In right-angled ΔACE,
![]() (I)
(I)
In right-angled ΔDCB,
![]() (II)
(II)
Adding equations (I) and (II),
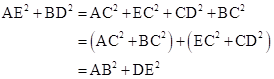
Solution 1(c)
Correct option: (i) AC × BC
 (I)
(I)
*Back answer is option (ii).
Solution 1(d)
Correct option: (iv) AB2
ΔABC is an isosceles triangle right-angled at C.
Therefore,
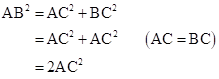
Solution 2
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
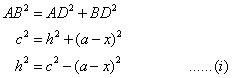
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
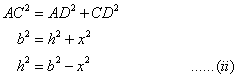
From (i) and (ii) we get,
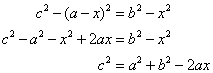
Hence Proved.
Solution 3
_files/20141015112304_image004.jpg)
In equilateral Δ ABC, AD ![]() BC.
BC.
Therefore, BD = DC = x/2 cm.
_files/20141015112304_image006.gif)
Solution 4
The pictorial form of the given problem is as follows,

Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
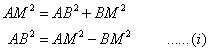
Now, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
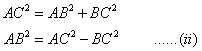
From (i) and (ii) we get,

Solution 5
We draw , PM,MN,NR
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Since, M andN are the mid-points of the sides QR and PQ respectively, therefore, PN=NQ,QM=RM
(i)
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
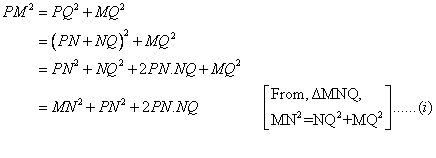
Now, we consider the ![]() and applying Pythagoras
and applying Pythagoras
theorem we get,
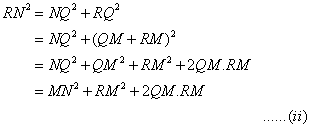
Adding (i) and (ii) we get,
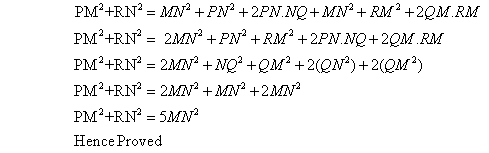
(ii)
We consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
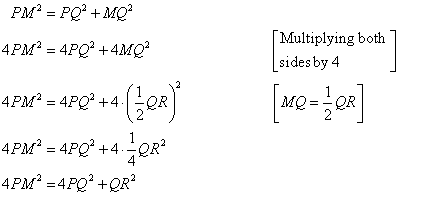
![]() .
.
(iii)
We consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
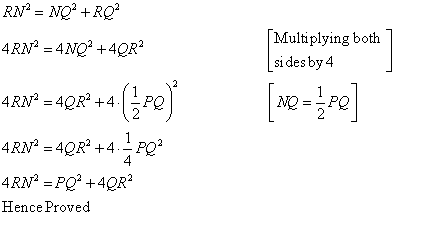
(iv)
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
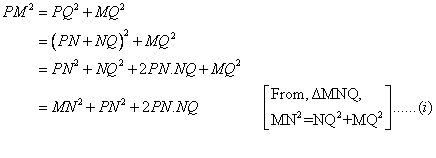
Now, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
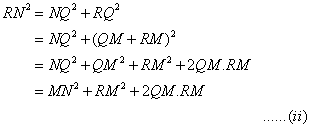
Adding (i) and (ii) we get,
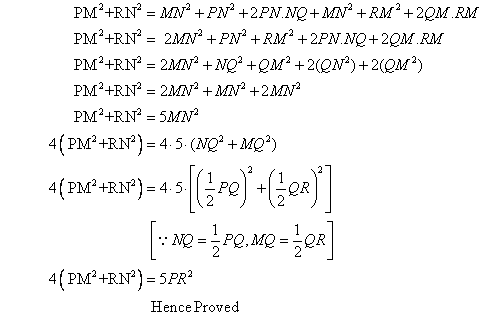
Solution 6
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
In triangle ABC, ![]() B = 90o and D is the mid-point of BC. Join AD. Therefore, BD=DC
B = 90o and D is the mid-point of BC. Join AD. Therefore, BD=DC
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
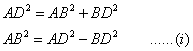
Similarly, we get from rt. angle triangles ABC we get,
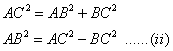
From (i) and (ii) ,

Solution 7
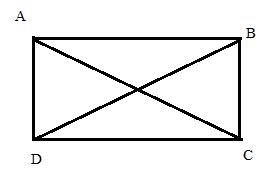
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Since, ABCD is a rectangle angles A,B,C and D are rt. angles.
First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
![]()
Similarly, we get from rt. angle triangle BDC we get,

Adding (i) and (ii) ,
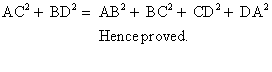
Solution 8
_files/20141015112304_image010.jpg)
_files/20141015112304_image012.gif)
Solution 9
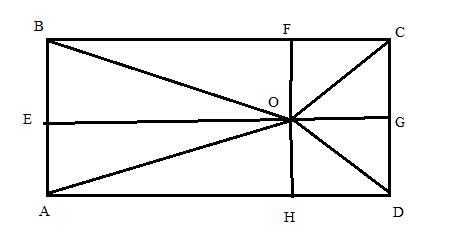
Draw rectangle ABCD with arbitrary point O within it, and then draw lines OA, OB, OC, OD. Then draw lines from point O perpendicular to the sides: OE, OF, OG, OH.
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Using Pythagorean theorem we have from the above diagram:
OA2 = AH2 + OH2 = AH2 + AE2
OC2 = CG2 + OG2 = EB2 + HD2
OB2 = EO2 + BE2 = AH2 + BE2
OD2 = HD2 + OH2 = HD2 + AE2
Adding these equalities we get:
OA2 + OC2 = AH2 + HD2 + AE2 + EB2
OB2 + OD2 = AH2 + HD2 + AE2 + EB2
From which we prove that for any point within the rectangle there is the relation
OA2 + OC2 = OB2 + OD2
Hence Proved.
Solution 10
Here, we first need to join OA, OB, and OC after which the figure becomes as follows,
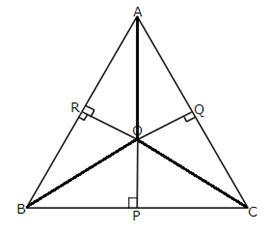
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides. First, we consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
Similarly, from triangles, BPO,COQ,AOQ,CPO and BRO we get the following results,
Adding (i), (ii) and (iii),we get
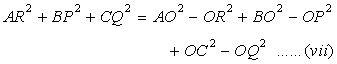
Adding (iv), (v) and (vi),we get ,
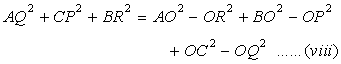
From (vii) and (viii), we get,
AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2
Hence proved.
Pythagoras Theorem [Proof and Simple Applications with Converse] Exercise Test Yourself
Solution 1
Take M be the point on CD such that AB = DM.
So DM = 7cm and MC = 10 cm
Join points B and M to form the line segment BM.
So BM || AD also BM = AD.
_files/20141015105311_image003.jpg)
_files/20141015105311_image005.gif)
Solution 2
Given that AX: XB = 1: 2 = AY: YC.
Let x be the common multiple for which this proportion gets satisfied.
So, AX = 1x and XB = 2x
AX + XB = 1x + 2x = 3x
⇒ AB = 3x .….(A - X - B)
⇒ 12 = 3x
⇒ x = 4
AX = 1x = 4 and XB = 2x = 2 × 4 = 8
Similarly,
AY = 1y and YC = 2y
AY = 8…(given)
⇒ 8 = y
∴ YC = 2y = 2 × 8 = 16
∴ AC = AY + YC = 8 + 16 = 24 cm
∆ABC is a right angled triangle. …. Given
∴ By Pythagoras Theorem, we get
⇒ AB2 + BC2 = AC2
⇒ BC2 = AC2 - AB2
⇒ BC2 = (24)2 - (12)2
⇒ BC2 = 576 - 144
⇒ BC2 = 432
⇒ BC= ![]() cm
cm
∴ AC = 24 cm and BC =![]() cm
cm
Solution 3
_files/20141015105311_image016.jpg)
_files/20141015105311_image018.gif)
_files/20141015105311_image020.gif)
Solution 4
PQRS is a rhombus with side length 10 cm
Diagonal QS = 16 cm

Now, all sides of a rhombus are equal and diagonals of a rhombus bisect each other at right angles.
Then, SO = QO = 8 cm
So, in right-angled triangle POQ,
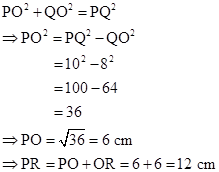
Therefore, the length of other diagonal of rhombus is 12 cm.
Solution 5
In right-angled ΔAOB,
![]() (I)
(I)
In right-angled ΔCOD,
![]() (II)
(II)
In right-angled ΔAOD,
![]() (III)
(III)
In right-angled ΔBOC,
![]() (IV)
(IV)
Adding equations (I) and (II),
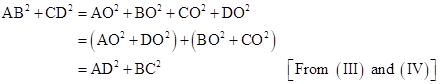
Solution 6
_files/20141015112304_image016.jpg)
Diagonals of the rhombus are perpendicular to each other.
_files/20141015112304_image018.gif)
Solution 7
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
We consider the ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
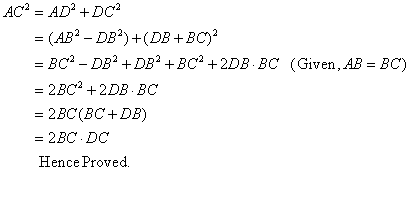
Solution 8

In an isosceles triangle ABC; AB = AC and D is point on BC produced. Construct AE perpendicular BC.
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
We consider the rt. angled ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
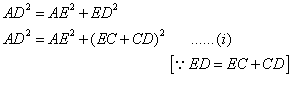
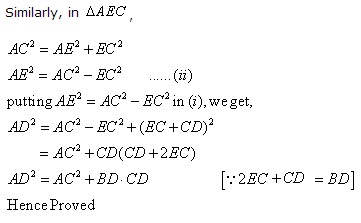
Solution 9
Pythagoras theorem states that in a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
We consider the rt. angled ![]() and applying Pythagoras theorem we get,
and applying Pythagoras theorem we get,
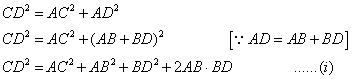
Similarly, in ![]() ,
,
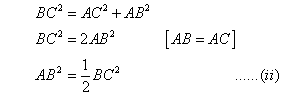
Putting, ![]() from (ii) in (i) we get,
from (ii) in (i) we get,

Hence Proved.
Solution 10
_files/20141015112304_image020.jpg)
_files/20141015112304_image022.gif)
Solution 11
Here,
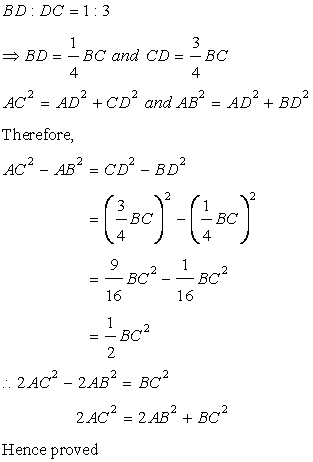
Solution 12
Construction: Draw median AP.
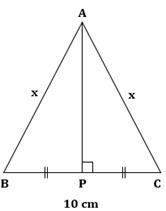
In ΔABC, AB = AC = x and BC = 10 cm
So, ABC is an isosceles triangle.
BP = CP (AP is the median)
Now, median of an isosceles triangle is also perpendicular to the base.
∴ AP ⊥ BC
Also,
A(ΔABC) = 60 cm2
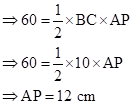
Now, in right-angled ΔAPC,
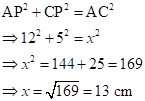
Solution 13
In right-angled DADB,
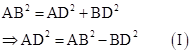
In right-angled ΔADC,
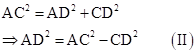
From equations (I) and (II),
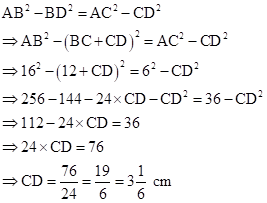
Hence, the length
of CD is ![]() cm.
cm.
Solution 14
ABCD is a quadrilateral in which ∠A + ∠D = 90o
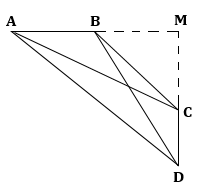
Construction: Extend AB and DC and let them intersect at point M.
In ΔAMD, ∠A + ∠D = 90o
⇒ ∠M = 90o
Now,
In right-angled ΔAMC,
![]()
In right-angled ΔBMD,
![]()
In right-angled ΔAMD,
![]()
In right-angled ΔBMC,
![]()
Adding equations (I) and (II),

