Class 9 SELINA Solutions Maths Chapter 10: Isosceles Triangle
Isosceles Triangle Exercise Ex. 10(A)
Solution 1(a)
Correct option: (i) AB = AC
In ∆BAD and ∆CAD
∠B = ∠C
∠BAD = ∠CAD
AD is common
Hence,
∆BAD ≅ ∆CAD … (A.A.S.)
∴ AB = AC … (c.p.c.t.)
Solution 1(b)
Correct option: (ii) BD = CD
In ∆BAD and ∆CAD
AB = AC … given
AD common
∠ADB = ∠ADC … (each 90o)
∆BAD ≅ ∆CAD … (R.H.S.)
∴ BD = CD … (c.p.c.t.)
Solution 1(c)
Correct option: (iv) 28°
∆ADB is isosceles triangle
∴ ∠ABD = ∠BAD = 65o
Now,
∠ADC = ∠ABD + ∠BAD …(external angle theorem)
∴ ∠ADC = 130o
In ∆ADC,
∠ADC + ∠DAC + ∠ACD = 180 … (sum of angles in a triangle)
130 + 22 + ∠ACD = 180
∠ACD = 28o
Solution 1(d)
Correct option: (iii) AD = AE
∆ABC is isosceles triangle
∴ ∠ABD = ∠ACE
Now, in ∆ABD and ∆ACE
AB = AC
∠ABD = ∠ACE
Now,
BE = DC
BD + DE = DE + EC
BD = EC
∆ABD ≅ ∆ACE … (S.A.S.)
Solution 1(e)
Correct option: (i) isosceles but not congruent
In ΔABC and ΔPQR,
AB = AC,
∴ ΔABC is isosceles
∠C = ∠B …(1)
Also,
∠C = ∠P …(2)
∠B = ∠Q …(3)
∴∠P = ∠Q … (from (1), (2) and (3))
∴ ΔPQR is isosceles
But, we can't prove ΔABC ≅ ΔPQR using the given data.
Therefore, triangles are isosceles but not congruent.
Solution 2
In ![]()
![]() BAC +
BAC + ![]() ACB +
ACB + ![]() ABC = 1800
ABC = 1800
480 + ![]() ACB +
ACB + ![]() ABC = 1800
ABC = 1800
But ![]() ACB =
ACB = ![]() ABC[AB = AC]
ABC[AB = AC]
2![]() ABC = 1800 - 480
ABC = 1800 - 480
2![]() ABC = 1320
ABC = 1320
![]() ABC = 660 =
ABC = 660 = ![]() ACB ……(i)
ACB ……(i)
![]() ACB = 660
ACB = 660
![]() ACD +
ACD + ![]() DCB = 660
DCB = 660
180 + ![]() DCB = 660
DCB = 660
![]() DCB = 480………(ii)
DCB = 480………(ii)
Now, In ![]()
![]() DBC = 660[From (i), Since
DBC = 660[From (i), Since ![]() ABC =
ABC = ![]() DBC]
DBC]
![]() DCB = 480[From (ii)]
DCB = 480[From (ii)]
![]() BDC = 1800 - 480 - 660
BDC = 1800 - 480 - 660
![]() BDC = 660
BDC = 660
Since ![]() BDC =
BDC = ![]() DBC
DBC
Therefore,BC = CD
Equal angles have equal sides opposite to them.
Solution 3
Given: ![]() ACE = 1300; AD = BD = CD
ACE = 1300; AD = BD = CD
Proof:
(i)

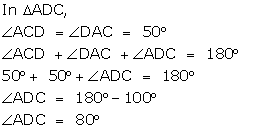
(ii)

(iii)
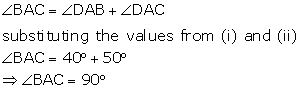
Solution 4


(i)
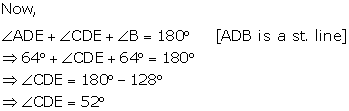
(ii)

Solution 5
(i) Let the triangle be ABC and the altitude be AD.



(ii) Let triangle be ABC and altitude be AD.
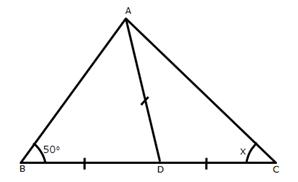


Solution 6
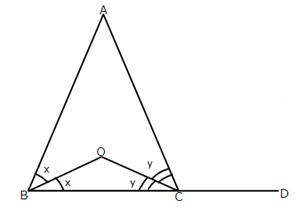
Let ![]() ABO =
ABO =![]() OBC = x and
OBC = x and ![]() ACO =
ACO = ![]() OCB = y
OCB = y
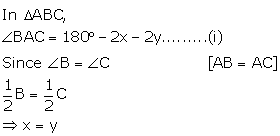
Now,

Solution 7
Given: ![]()
(i) We know that the sum of the measure of all the angles of a quadrilateral is 360o.
In quad. PQNL,
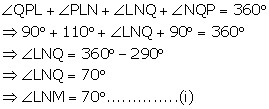

(ii)
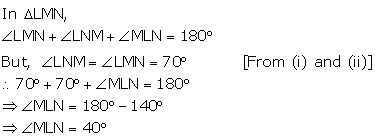
Solution 8


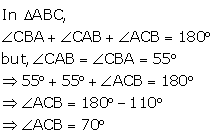
Now,

Solution 9
Let us name the figure as following:
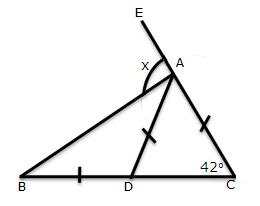
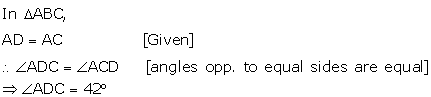

For x:

Solution 10

Therefore,
AD=DC
![]()
and AB = BC
![]()
Substituting the value of x from (i)
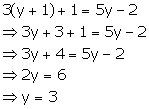
Putting y = 3 in (i)
x = 3 + 1
![]() x = 4
x = 4
Solution 11
Let P and Q be the points as shown below:
Given: ![]()



Solution 12

Now,
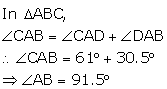
Solution 13


Solution 14
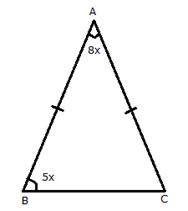
Let ![]()
Given: AB = AC
![]() [Angles opp. to equal sides are equal]
[Angles opp. to equal sides are equal]

Solution 15
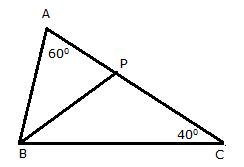
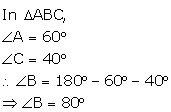
Now,
BP is the bisector of ![]()
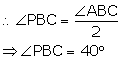
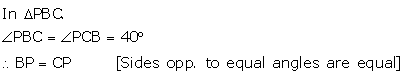
Isosceles Triangle Exercise Ex. 10(B)
Solution 1(a)
Correct option: (ii) ΔABD ≅ ΔFEC
In ∆ABD and ∆FEC
AB = EF
BC =DE
∴ BC + CD = DE + CD
∴ BD = EC
∠B = ∠E … (both 90o)
∆ABD ≅ ∆FEC … (S.A.S.)
Solution 1(b)
Correct option: (iii) PQ = PR
In ∆PQO and ∆PRO
∠PQO = ∠PRO … (each 90o)
∠POQ = ∠POR … given
PO is common
∆PQO ≅ ∆PRO … (A.A.S.)
PQ = PR … (c.p.c.t.)
Solution 1(c)
Correct option: (iv) x = 16, y = 8
∠A = ∠C
∴ ∆ABC is isosceles
∴ AB = BC
∴ 2x = 3y+8 … (1)
Also, in ∆ABD and ∆CBD
∠ABD = ∠CBD … given
AB = BC … given
BD is common
∆ ABD ≅ ∆ CBD … (S.A.S.)
∴ AD = CD … (c.p.c.t.)
∴ x = 2y …(2)
From (1) and (2)
4y = 3y + 8
y = 8
x = 16
Solution 1(d)
Correct option: (iv) ∆ABX ≅ ∆BAY
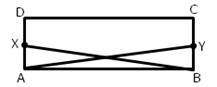
In ∆ABX and ∆BAY
∠XAB = ∠YBA … (each 90o)
AX = BY … given
AB is common
∆ ABX ≅ ∆BAY … (S.A.S.)
Solution 1(e)
Correct option: (ii) ∠PBC = ∠PCB
Assuming that quadrilateral ABCD is a Square
We have
DC = AB
∠CDP = ∠BAP … (each 90o)
DP = AP … (P is mid-point of side AD)
Hence,
In ∆ CDP and ∆BAP
We can say that
∆ CDP ≅ ∆BAP … (S.A.S.)
CP = BP … (c.p.c.t.)
Now, in ∆BPC
We have
CP = BP
Hence, ∆BPC is isosceles
∴ ∠PBC = ∠PCB
Solution 2
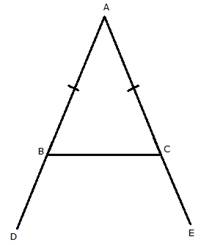
Const: AB is produced to D and AC is produced to E so that exterior angles ![]() and
and ![]() is formed.
is formed.
Since angle B and angle C are acute they cannot be right angles or obtuse angles.

Now,

Therefore, exterior angles formed are obtuse and equal.
Solution 3
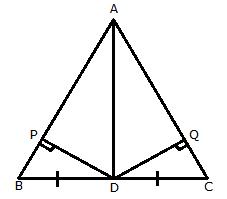
Const: Join AD.
(i)

(ii) We have already proved that ![]()
Therefore,BP = CQ[cpct]
Now,
AB = AC[Given]
![]() AB - BP = AC - CQ
AB - BP = AC - CQ
![]() AP = AQ
AP = AQ
(iii)
Hence, AD bisects angle A.
Solution 4
(i)

(ii)Since ![]()
![]()
Solution 5
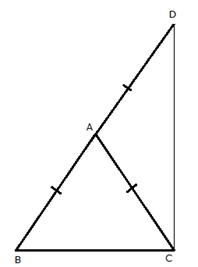
Const: Join CD.

Adding (i) and (ii)
![]()

Solution 6(i)
_SHR_files/20140924122808_image006.jpg)
_SHR_files/20140924122808_image008.gif)
Solution 6(ii)

Given:
AD is the angle bisector of ∠BAC, hence ∠BAD = ∠DAC
Also, AD bisects BC, hence BD = DC.
To prove: ∆ABC is isosceles, i.e. AB = AC
Proof:
In ∆ABC
BD = DC … (given)
Now by angle bisector theorem
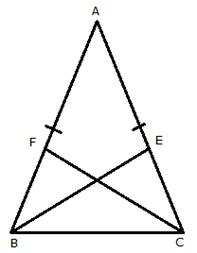
Solution 7
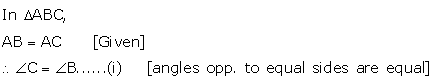
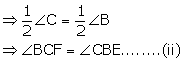
Solution 8
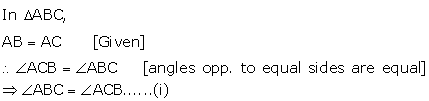
![]() DBC =
DBC = ![]() ECB = 90o[Given]
ECB = 90o[Given]
![]()
![]() DBC =
DBC = ![]() ECB …….(ii)
ECB …….(ii)
Subtracting (i) from (ii)
![]()
Solution 9
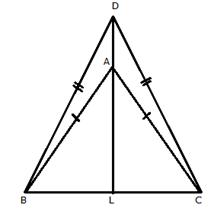
DA is produced to meet BC in L.
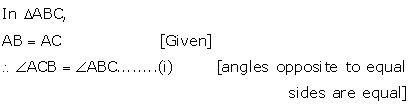

Subtracting (i) from (ii)
![]()
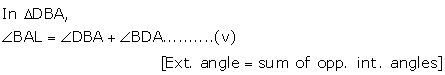
From (iii), (iv) and (v)
![]()
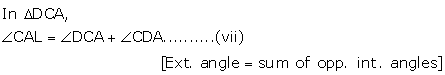
From (vi) and (vii)
![]()
Now,
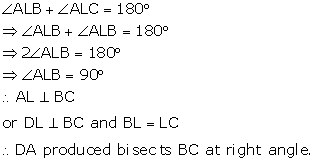
Solution 10
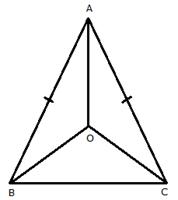
In ![]() ABC, we have AB = AC
ABC, we have AB = AC
![]()
![]() B =
B = ![]() C [angles opposite to equal sides are equal]
C [angles opposite to equal sides are equal]
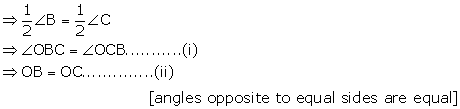
Now,
In ![]() ABO and
ABO and ![]() ACO,
ACO,
AB = AC[Given]
![]() OBC =
OBC = ![]() OCB[From (i)]
OCB[From (i)]
OB = OC[From (ii)]

Therefore, AO bisects ![]() BAC.
BAC.
Solution 11
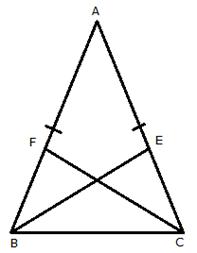
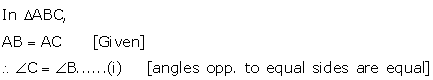

Solution 12

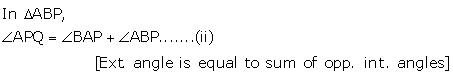
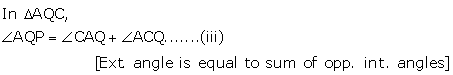
From (i), (ii) and (iii)
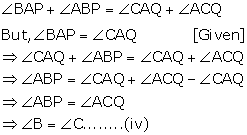
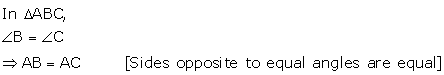
Solution 13
Since AE || BC and DAB is the transversal
![]()
Since AE || BC and AC is the transversal
![]()
But AE bisects ![]()
![]()
![]() AB = AC[Sides opposite to equal angles are equal]
AB = AC[Sides opposite to equal angles are equal]
Solution 14
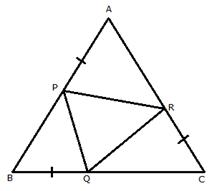
AB = BC = CA…….(i)[Given]
AP = BQ = CR…….(ii)[Given]
Subtracting (ii) from (i)
AB - AP = BC - BQ = CA - CR
BP = CQ = AR …………(iii)
![]() ……..(iv) [angles opp. to equal sides are equal]
……..(iv) [angles opp. to equal sides are equal]


From (v) and (vi)
PQ = QR = PR
Therefore, PQR is an equilateral triangle.
Solution 15
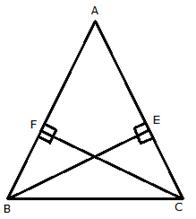
In ![]() ABE and
ABE and ![]() ACF,
ACF,
![]() A =
A = ![]() A[Common]
A[Common]
![]() AEB =
AEB = ![]() AFC = 900[Given: BE
AFC = 900[Given: BE ![]() AC; CF
AC; CF ![]() AB]
AB]
BE = CF[Given]
![]()
Therefore, ABC is an isosceles triangle.
Solution 16
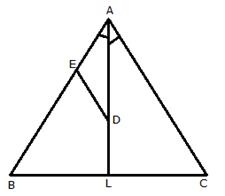
AL is bisector of angle A. Let D is any point on AL. From D, a straight line DE is drawn parallel to AC.
DE || AC[Given]
![]() ADE =
ADE = ![]() DAC….(i)[Alternate angles]
DAC….(i)[Alternate angles]
![]() DAC =
DAC = ![]() DAE…….(ii)[AL is bisector of
DAE…….(ii)[AL is bisector of ![]() A]
A]
From (i) and (ii)
![]() ADE =
ADE = ![]() DAE
DAE
![]() AE = ED[Sides opposite to equal angles are equal]
AE = ED[Sides opposite to equal angles are equal]
Therefore, AED is an isosceles triangle.
Solution 17
(i)
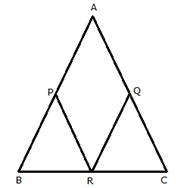
In ![]() ABC,
ABC,
AB = AC
![]()
![]() AP = AQ …….(i)[ Since P and Q are mid - points]
AP = AQ …….(i)[ Since P and Q are mid - points]
In ![]() BCA,
BCA,
PR = ![]() [PR is line joining the mid - points of AB and BC]
[PR is line joining the mid - points of AB and BC]
![]() PR = AQ……..(ii)
PR = AQ……..(ii)
In ![]() CAB,
CAB,
QR = ![]() [QR is line joining the mid - points of AC and BC]
[QR is line joining the mid - points of AC and BC]
![]() QR = AP……(iii)
QR = AP……(iii)
From (i), (ii) and (iii)
PR = QR
(ii)
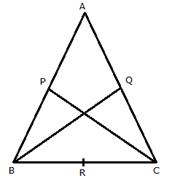
AB = AC
![]()
![]() B =
B = ![]() C
C
Also,

In ![]() BPC and
BPC and ![]() CQB,
CQB,
BP = CQ
![]() B =
B = ![]() C
C
BC = BC
Therefore, ΔBPC![]() ΔCQB [SAS]
ΔCQB [SAS]
BP = CP
Solution 18
(i) In ![]() ACB,
ACB,
AC = AC[Given]
![]()
![]() ABC =
ABC = ![]() ACB …….(i)[angles opposite to equal sides are equal]
ACB …….(i)[angles opposite to equal sides are equal]
![]() ACD +
ACD + ![]() ACB = 1800 …….(ii)[DCB is a straight line]
ACB = 1800 …….(ii)[DCB is a straight line]
![]() ABC +
ABC + ![]() CBE = 1800 ……..(iii)[ABE is a straight line]
CBE = 1800 ……..(iii)[ABE is a straight line]
Equating (ii) and (iii)
![]() ACD +
ACD + ![]() ACB =
ACB = ![]() ABC +
ABC + ![]() CBE
CBE
![]()
![]() ACD +
ACD + ![]() ACB =
ACB = ![]() ACB +
ACB + ![]() CBE[From (i)]
CBE[From (i)]
![]()
![]() ACD =
ACD = ![]() CBE
CBE
(ii)
Solution 19

AB is produced to E and AC is produced to F. BD is bisector of angle CBE and CD is bisector of angle BCF. BD and CD meet at D.
In ![]() ABC,
ABC,
AB = AC[Given]
![]()
![]() C =
C = ![]() B[angles opposite to equal sides are equal]
B[angles opposite to equal sides are equal]
![]() CBE = 1800 -
CBE = 1800 - ![]() B[ABE is a straight line]
B[ABE is a straight line]
![]() [BD is bisector of
[BD is bisector of ![]() CBE]
CBE]
![]()
Similarly,
![]() BCF = 1800 -
BCF = 1800 - ![]() C[ACF is a straight line]
C[ACF is a straight line]
![]() [CD is bisector of
[CD is bisector of ![]() BCF]
BCF]
![]()
Now,
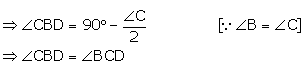
In ![]() BCD,
BCD,
![]()
![]() BD = CD
BD = CD
In ![]() ABD and
ABD and ![]() ACD,
ACD,
AB = AC[Given]
AD = AD[Common]
BD = CD[Proved]
Therefore, AD bisects![]() A.
A.
Solution 20

In ![]() ABC,
ABC,
CX is the angle bisector of ![]() C
C
![]()
![]() ACY =
ACY = ![]() BCX ....... (i)
BCX ....... (i)
In ![]() AXY,
AXY,
AX = AY[Given]
![]() AXY =
AXY = ![]() AYX …….(ii)[angles opposite to equal sides are equal]
AYX …….(ii)[angles opposite to equal sides are equal]
Now ![]() XYC =
XYC = ![]() AXB = 180°[straight line]
AXB = 180°[straight line]
![]()
![]() AYX +
AYX + ![]() AYC =
AYC = ![]() AXY +
AXY + ![]() BXY
BXY
![]()
![]() AYC =
AYC = ![]() BXY ........ (iii)[From (ii)]
BXY ........ (iii)[From (ii)]
In ![]() AYC and
AYC and ![]() BXC
BXC
![]() AYC +
AYC + ![]() ACY +
ACY + ![]() CAY =
CAY = ![]() BXC +
BXC + ![]() BCX +
BCX + ![]() XBC = 180°
XBC = 180°
![]()
![]() CAY =
CAY = ![]() XBC[From (i) and (iii)]
XBC[From (i) and (iii)]
![]()
![]() CAY =
CAY = ![]() ABC
ABC
Isosceles Triangle Exercise Test Yourself
Solution 1
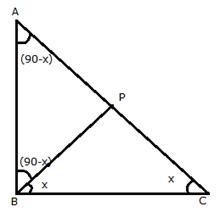
Let ![]() PBC =
PBC = ![]() PCB = x
PCB = x
In the right angled triangle ABC,
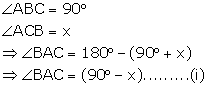
and
![]()
Therefore in the triangle ABP;
![]()
Hence,
PA = PB [sides opp. to equal angles are equal]
Solution 2

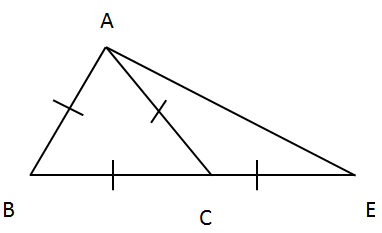
Solution 3

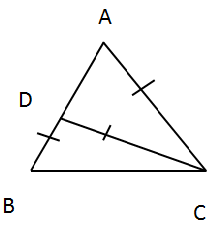
Solution 4

Solution 5
(i) In ΔABC, let the altitude AD bisects ∠BAC.
Then we have to prove that the ΔABC is isosceles.
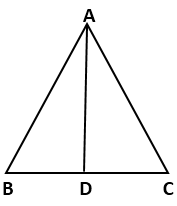
In triangles ADB and ADC,
∠BAD = ∠CAD (AD is bisector of ∠BAC)
AD = AD (common)
∠ADB = ∠ADC (Each equal to 90°)
⇒ ΔADB ≅ ΔADC (by ASA congruence criterion)
⇒ AB = AC (cpct)
Hence, ΔABC is an isosceles.
(ii) In Δ ABC, the bisector of ∠ BAC is perpendicular to the base BC. We have to prove that the ΔABC is isosceles.
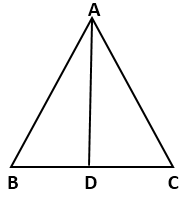
In triangles ADB and ADC,
∠BAD = ∠CAD (AD is bisector of ∠BAC)
AD = AD (common)
∠ADB = ∠ADC (Each equal to 90°)
⇒ ΔADB ≅ ΔADC (by ASA congruence criterion)
⇒ AB = AC (cpct)
Hence, ΔABC is an isosceles.
Solution 6
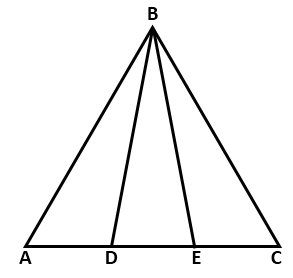
In ΔABC,
AB = BC (given)
⇒ ∠BCA = ∠BAC (Angles opposite to equal sides are equal)
⇒ ∠BCD = ∠BAE ….(i)
Given, AD = EC
⇒ AD + DE = EC + DE (Adding DE on both sides)
⇒ AE = CD ….(ii)
Now, in triangles ABE and CBD,
AB = BC (given)
∠BAE = ∠BCD [From (i)]
AE = CD [From (ii)]
⇒ ΔABE ≅ ΔCBD
⇒ BE = BD (cpct)
Solution 7
Since IA || CP and CA is a transversal
![]()
![]() CAI =
CAI = ![]() PCA[Alternate angles]
PCA[Alternate angles]
Also, IA || CP and AP is a transversal
![]()
![]() IAB =
IAB = ![]() APC[Corresponding angles]
APC[Corresponding angles]
But ![]()
![]() CAI =
CAI = ![]() IAB[Given]
IAB[Given]
![]()
![]() PCA =
PCA = ![]() APC
APC
![]() AC = AP
AC = AP
Similarly,
BC = BQ
Now,
PQ = AP + AB + BQ
= AC + AB + BC
= Perimeter of ![]() ABC
ABC
Solution 8
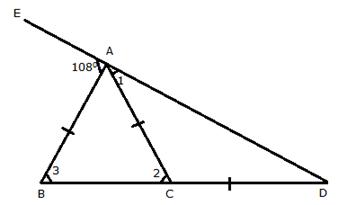
In ![]() ABD,
ABD,
![]() BAE =
BAE = ![]() 3 +
3 + ![]() ADB
ADB
![]() 1080 =
1080 = ![]() 3 +
3 + ![]() ADB
ADB
But AB = AC
![]()
![]() 3 =
3 = ![]() 2
2
![]() 1080 =
1080 = ![]() 2 +
2 + ![]() ADB ……(i)
ADB ……(i)
Now,
In ![]() ACD,
ACD,
![]() 2=
2=![]() 1+
1+ ![]() ADB
ADB
But AC = CD
![]()
![]() 1 =
1 = ![]() ADB
ADB
![]()
![]() 2 =
2 = ![]() ADB +
ADB + ![]() ADB
ADB
![]()
![]() 2 = 2
2 = 2![]() ADB
ADB
Putting this value in (i)
![]() 1080 = 2
1080 = 2![]() ADB +
ADB + ![]() ADB
ADB
![]() 3
3![]() ADB = 1080
ADB = 1080
![]()
![]() ADB = 360
ADB = 360
Solution 9

Solution 10
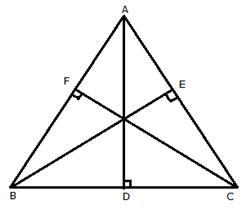
In right ![]() BEC and
BEC and ![]() BFC,
BFC,
BE = CF[Given]
BC = BC[Common]
![]() BEC =
BEC = ![]() BFC[each = 900]
BFC[each = 900]
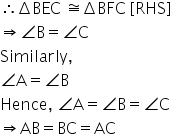
Therefore, ABC is an equilateral triangle.
Solution 11
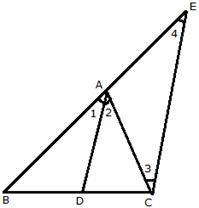
DA || CE[Given]
![]() [Corresponding angles]
[Corresponding angles]
![]() [Alternate angles]
[Alternate angles]
But ![]() [ AD is the bisector of
[ AD is the bisector of ![]() A]
A]
From (i), (ii) and (iii)
![]()
![]() AC = AE
AC = AE
![]()
![]() ACE is an isosceles triangle.
ACE is an isosceles triangle.
Solution 12
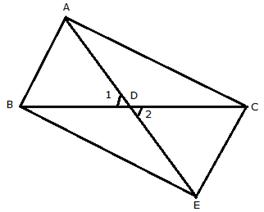
Produce AD upto E such that AD = DE.
Hence, ABC is an isosceles triangle.
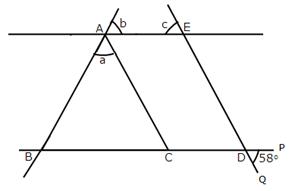
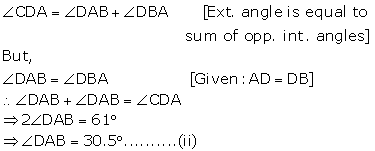
Solution 13
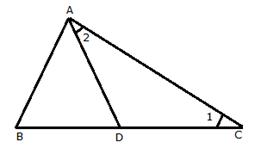
Since AB = AD = BD
![]() is an equilateral triangle.
is an equilateral triangle.
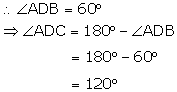
Again in![]()
AD = DC
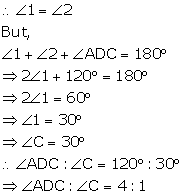
Solution 14
(i)
_SHR_files/20140924122808_image022.gif)
(ii)
_SHR_files/20140924122808_image024.jpg)
_SHR_files/20140924122808_image026.gif)








