Class 9 SELINA Solutions Maths Chapter 11: Inequalities
Inequalities Exercise Ex. 11
Solution 1(a)
Correct option: (ii) BC > AB
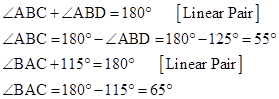
In DABC,
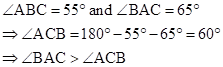
If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.
![]()
Solution 1(b)
Correct option: (iii) BD > DC
BD = AD [Given]
![]()
In ΔABD,
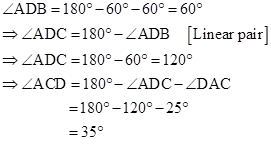
If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.
So, in ΔADC,
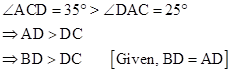
Solution 1(c)
Correct option: (iv) BD > CD
AB = AC [Given]
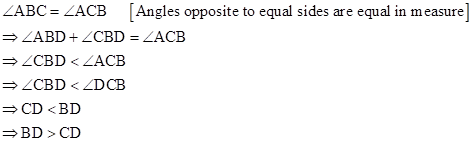
Solution 1(d)
Correct option: (ii) BD < AB
In ΔABC,
![]()
Given, ![]()
And,
![]()
Now, in ΔABD,
![]()
If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.
Here,
![]()
Solution 1(e)
Correct option: (ii) AC > AB

If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.
In ΔABC,
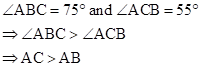
Solution 1(f)
Correct option: (i) AB + BC + CD + DA > AC + BD
Consider quadrilateral ABCD as follows:
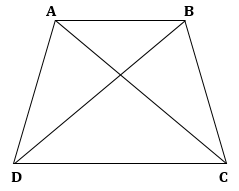
The sum of the lengths of any two sides of a triangle is always greater than the third side.
AB + BC > AC (I)
BC + CD > BD (II)
CD + DA > AC (III)
DA + AB > BD (IV)
Adding equations (I), (II), (III), (IV),
2AB + 2BC + 2CD + 2DA > 2AC + 2BD
⇒ 2(AB + BC + CD + DA) > 2(AC + BD)
⇒ AB + BC + CD + DA > AC + BD
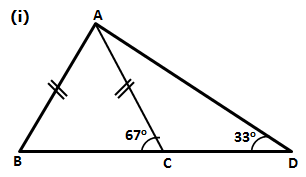
Solution 2
In ![]() ABC,
ABC,
AB = AC[Given]
![]()
![]() ACB =
ACB = ![]() B[angles opposite to equal sides are equal]
B[angles opposite to equal sides are equal]
![]() B = 700[Given]
B = 700[Given]
![]()
![]() ACB = 700 ……….(i)
ACB = 700 ……….(i)
Now,
![]() ACB +
ACB +![]() ACD = 1800[ BCD is a straight line]
ACD = 1800[ BCD is a straight line]
![]() 700 +
700 + ![]() ACD = 1800
ACD = 1800
![]()
![]() ACD = 1100 …………(ii)
ACD = 1100 …………(ii)
In ![]() ACD,
ACD,
![]() CAD +
CAD + ![]() ACD +
ACD + ![]() D = 1800
D = 1800
![]()
![]() CAD + 1100 +
CAD + 1100 + ![]() D = 1800 [From (ii)]
D = 1800 [From (ii)]
![]()
![]() CAD +
CAD + ![]() D = 700
D = 700
But ![]() D = 400 [Given]
D = 400 [Given]
![]()
![]() CAD + 400= 700
CAD + 400= 700
![]()
![]() CAD = 300 ………………(iii)
CAD = 300 ………………(iii)
In ![]() ACD,
ACD,
![]() ACD = 1100[From (ii)]
ACD = 1100[From (ii)]
![]() CAD = 300[From (iii)]
CAD = 300[From (iii)]
![]() D = 400 [Given]
D = 400 [Given]
![]()
[Greater angle has greater side opposite to it]
Also,
AB = AC[Given]
Therefore, AB > CD.
Solution 3
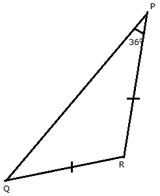
In ![]() PQR,
PQR,
QR = PR[Given]
![]()
![]() P =
P = ![]() Q[angles opposite to equal sides are equal]
Q[angles opposite to equal sides are equal]
![]() P = 360[Given]
P = 360[Given]
![]()
![]() Q = 360
Q = 360
In ![]() PQR,
PQR,
![]() P +
P + ![]() Q +
Q + ![]() R = 1800
R = 1800
![]() 360 + 360 +
360 + 360 + ![]() R = 1800
R = 1800
![]()
![]() R + 720 = 1800
R + 720 = 1800
![]()
![]() R = 1080
R = 1080
Now,
![]() R = 1080
R = 1080
![]() P = 360
P = 360
![]() Q = 360
Q = 360
Since ![]() R is the greatest, therefore, PQ is the largest side.
R is the greatest, therefore, PQ is the largest side.
Solution 4
The sum of any two sides of the triangle is always greater than third side of the triangle.
Third side < 13![]() +
+![]() 8 =
8 =![]() 21 cm.
21 cm.
The difference between any two sides of the triangle is always less than the third side of the triangle.
Third side > 13![]() -
-![]() 8 =
8 =![]() 5 cm.
5 cm.
Therefore, the length of the third side is between 5 cm and 9 cm, respectively.
The value of a =![]() 5 cm and b
5 cm and b![]() = 21
= 21![]() cm.
cm.
Solution 5

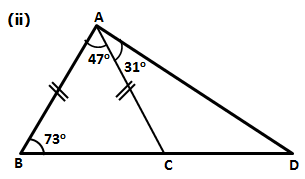
Solution 6
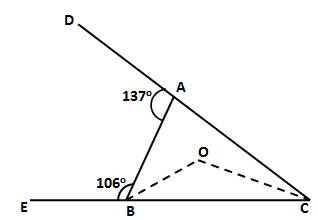

Solution 7

Solution 8
In ![]() BEC,
BEC,
![]() B +
B + ![]() BEC +
BEC + ![]() BCE = 1800
BCE = 1800
![]() B = 650 [Given]
B = 650 [Given]
![]() BEC = 900[CE is perpendicular to AB]
BEC = 900[CE is perpendicular to AB]
![]() 650 + 900 +
650 + 900 + ![]() BCE = 1800
BCE = 1800
![]()
![]() BCE = 1800 - 1550
BCE = 1800 - 1550
![]()
![]() BCE = 250 =
BCE = 250 = ![]() DCF …………(i)
DCF …………(i)
In ![]() CDF,
CDF,
![]() DCF +
DCF + ![]() FDC +
FDC + ![]() CFD = 1800
CFD = 1800
![]() DCF = 250 [From (i)]
DCF = 250 [From (i)]
![]() FDC = 900[AD is perpendicular to BC]
FDC = 900[AD is perpendicular to BC]
![]() 250 + 900 +
250 + 900 + ![]() CFD = 1800
CFD = 1800
![]()
![]() CFD = 1800 - 1150
CFD = 1800 - 1150
![]()
![]() CFD = 650 …………(ii)
CFD = 650 …………(ii)
Now, ![]() AFC +
AFC + ![]() CFD = 1800[AFD is a straight line]
CFD = 1800[AFD is a straight line]
![]()
![]() AFC + 650 = 1800
AFC + 650 = 1800
![]()
![]() AFC = 1150 ………(iii)
AFC = 1150 ………(iii)
In ![]() ACE,
ACE,
![]() ACE +
ACE + ![]() CEA +
CEA + ![]() BAC = 1800
BAC = 1800
![]() BAC = 600 [Given]
BAC = 600 [Given]
![]() CEA = 900[CE is perpendicular to AB]
CEA = 900[CE is perpendicular to AB]
![]()
![]() ACE + 900 + 600 = 1800
ACE + 900 + 600 = 1800
![]()
![]() ACE = 1800 - 1500
ACE = 1800 - 1500
![]()
![]() ACE = 300 …………(iv)
ACE = 300 …………(iv)
In ![]() AFC,
AFC,
![]() AFC +
AFC + ![]() ACF +
ACF + ![]() FAC = 1800
FAC = 1800
![]() AFC = 1150 [From (iii)]
AFC = 1150 [From (iii)]
![]() ACF = 300[From (iv)]
ACF = 300[From (iv)]
![]() 1150 + 300 +
1150 + 300 + ![]() FAC = 1800
FAC = 1800
![]()
![]() FAC = 1800 - 1450
FAC = 1800 - 1450
![]()
![]() FAC = 350 …………(v)
FAC = 350 …………(v)
In ![]() AFC,
AFC,
![]() FAC = 350[From (v)]
FAC = 350[From (v)]
![]() ACF = 300[From (iv)]
ACF = 300[From (iv)]
![]()
In ![]() CDF,
CDF,
![]() DCF = 250[From (i)]
DCF = 250[From (i)]
![]() CFD = 650[From (ii)]
CFD = 650[From (ii)]
![]()
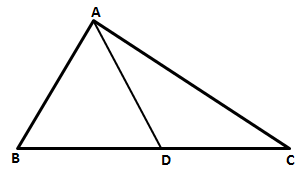
Solution 9
![]() ACB = 740 …..(i)[Given]
ACB = 740 …..(i)[Given]
![]() ACB +
ACB + ![]() ACD = 1800[BCD is a straight line]
ACD = 1800[BCD is a straight line]
![]() 740 +
740 + ![]() ACD = 1800
ACD = 1800
![]()
![]() ACD = 1060 ……..(ii)
ACD = 1060 ……..(ii)
In ![]() ACD,
ACD,
![]() ACD +
ACD + ![]() ADC+
ADC+ ![]() CAD = 1800
CAD = 1800
Given that AC = CD
![]()
![]() ADC=
ADC= ![]() CAD
CAD
![]() 1060 +
1060 + ![]() CAD +
CAD + ![]() CAD = 1800[From (ii)]
CAD = 1800[From (ii)]
![]() 2
2![]() CAD = 740
CAD = 740
![]()
![]() CAD = 370 =
CAD = 370 =![]() ADC………..(iii)
ADC………..(iii)
Now,
![]() BAD = 1100[Given]
BAD = 1100[Given]
![]() BAC +
BAC + ![]() CAD = 1100
CAD = 1100
![]() BAC + 370 = 1100
BAC + 370 = 1100
![]() BAC = 730 ……..(iv)
BAC = 730 ……..(iv)
In ![]() ABC,
ABC,
![]() B +
B + ![]() BAC+
BAC+ ![]() ACB = 1800
ACB = 1800
![]()
![]() B + 730 + 740 = 1800[From (i) and (iv)]
B + 730 + 740 = 1800[From (i) and (iv)]
![]()
![]() B + 1470 = 1800
B + 1470 = 1800
![]()
![]() B = 330 ………..(v)
B = 330 ………..(v)
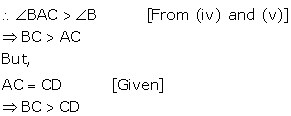
Solution 10
(i) ![]() ADC +
ADC + ![]() ADB = 1800[BDC is a straight line]
ADB = 1800[BDC is a straight line]
![]() ADC = 900[Given]
ADC = 900[Given]
900 + ![]() ADB = 1800
ADB = 1800
![]() ADB = 900 …………(i)
ADB = 900 …………(i)
In ![]() ADB,
ADB,
![]() ADB = 900[From (i)]
ADB = 900[From (i)]
![]()
![]() B +
B + ![]() BAD = 900
BAD = 900
Therefore, ![]() B and
B and ![]() BAD are both acute, that is less than 900.
BAD are both acute, that is less than 900.
![]() AB > BD …….(ii)[Side opposite 900 angle is greater than
AB > BD …….(ii)[Side opposite 900 angle is greater than
side opposite acute angle]
(ii) In ![]() ADC,
ADC,
![]() ADB = 900
ADB = 900
![]()
![]() C +
C + ![]() DAC = 900
DAC = 900
Therefore, ![]() C and
C and ![]() DAC are both acute, that is less than 900.
DAC are both acute, that is less than 900.
![]() AC > CD ……..(iii)[Side opposite 900 angle is greater than
AC > CD ……..(iii)[Side opposite 900 angle is greater than
side opposite acute angle]
Adding (ii) and (iii)
AB + AC > BD + CD
![]() AB + AC > BC
AB + AC > BC
Solution 11
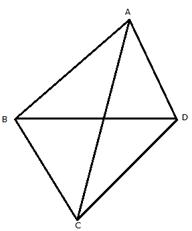
Const: Join AC and BD.
(i) In ![]() ABC,
ABC,
AB + BC > AC….(i)[Sum of two sides is greater than the
third side]
In ![]() ACD,
ACD,
AC + CD > DA….(ii)[ Sum of two sides is greater than the
third side]
Adding (i) and (ii)
AB + BC + AC + CD > AC + DA
AB + BC + CD > AC + DA - AC
AB + BC + CD > DA …….(iii)
(ii)In ![]() ACD,
ACD,
CD + DA > AC….(iv)[Sum of two sides is greater than the
third side]
Adding (i) and (iv)
AB + BC + CD + DA > AC + AC
AB + BC + CD + DA > 2AC
(iii) In ![]() ABD,
ABD,
AB + DA > BD….(v)[Sum of two sides is greater than the
third side]
In ![]() BCD,
BCD,
BC + CD > BD….(vi)[Sum of two sides is greater than the
third side]
Adding (v) and (vi)
AB + DA + BC + CD > BD + BD
AB + DA + BC + CD > 2BD
Solution 12
(i) In ![]() ABC,
ABC,
AB = BC = CA[ABC is an equilateral triangle]
![]()
![]() A =
A = ![]() B =
B = ![]() C
C
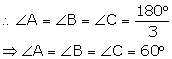
In ![]() ABP,
ABP,
![]() A = 600
A = 600
![]() ABP< 600
ABP< 600
![]()
[Side opposite to greater angle is greater]
(ii) In ![]() BPC,
BPC,
![]() C = 600
C = 600
![]() CBP< 600
CBP< 600
![]()
[Side opposite to greater angle is greater]
Solution 13
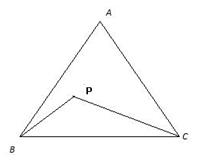
Let ![]() PBC = x and
PBC = x and ![]() PCB = y
PCB = y
then,
![]() BPC = 1800 - (x + y) ………(i)
BPC = 1800 - (x + y) ………(i)
Let ![]() ABP = a and
ABP = a and ![]() ACP = b
ACP = b
then,
![]() BAC = 1800 - (x + a) - (y + b)
BAC = 1800 - (x + a) - (y + b)
![]()
![]() BAC = 1800 - (x + y) - (a + b)
BAC = 1800 - (x + y) - (a + b)
![]()
![]() BAC =
BAC =![]() BPC - (a + b)
BPC - (a + b)
![]()
![]() BPC =
BPC = ![]() BAC + (a + b)
BAC + (a + b)
![]()
![]() BPC >
BPC > ![]() BAC
BAC
Solution 14
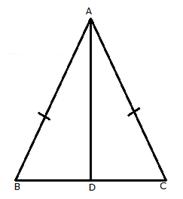
We know that exterior angle of a triangle is always greater than each of the interior opposite angles.
![]() In
In ![]() ABD,
ABD,
![]() ADC >
ADC > ![]() B ……..(i)
B ……..(i)
In ![]() ABC,
ABC,
AB = AC
![]()
![]() B =
B = ![]() C …..(ii)
C …..(ii)
From (i) and (ii)
![]() ADC >
ADC > ![]() C
C
(i) In ![]() ADC,
ADC,
![]() ADC >
ADC > ![]() C
C
![]() AC > AD ………(iii) [side opposite to greater angle is greater]
AC > AD ………(iii) [side opposite to greater angle is greater]
(ii) In ![]() ABC,
ABC,
AB = AC
![]() AB > AD[ From (iii)]
AB > AD[ From (iii)]
Solution 15
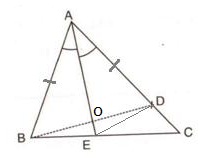
Const: Join ED.
In ![]() AOB and
AOB and ![]() AOD,
AOD,
AB = AD[Given]
AO = AO[Common]
![]() BAO =
BAO = ![]() DAO[AO is bisector of
DAO[AO is bisector of ![]() A]
A]
![]() [SAS criterion]
[SAS criterion]
Hence,
BO = OD………(i)[cpct]
![]() AOB =
AOB = ![]() AOD .……(ii)[cpct]
AOD .……(ii)[cpct]
![]() ABO =
ABO = ![]() ADO
ADO ![]()
![]() ABD =
ABD = ![]() ADB ………(iii)[cpct]
ADB ………(iii)[cpct]
Now,
![]() AOB =
AOB = ![]() DOE[Vertically opposite angles]
DOE[Vertically opposite angles]
![]() AOD =
AOD = ![]() BOE[Vertically opposite angles]
BOE[Vertically opposite angles]
![]()
![]() BOE =
BOE = ![]() DOE ……(iv)[From (ii)]
DOE ……(iv)[From (ii)]
(i) In ![]() BOE and
BOE and ![]() DOE,
DOE,
BO = CD[From (i)]
OE = OE[Common]
![]() BOE =
BOE = ![]() DOE[From (iv)]
DOE[From (iv)]
![]() [SAS criterion]
[SAS criterion]
Hence, BE = DE[cpct]
(ii) In ![]() BCD,
BCD,
![]() ADB =
ADB = ![]() C +
C + ![]() CBD[Ext. angle = sum of opp. int. angles]
CBD[Ext. angle = sum of opp. int. angles]
![]()
![]() ADB >
ADB > ![]() C
C
![]()
![]() ABD >
ABD > ![]() C[From (iii)]
C[From (iii)]
Inequalities Exercise Test Yourself
Solution 1
AB = AC (Given) (I)
⇒ ∠ABC = ∠ACB [Angles opposite to equal sides are equal]
⇒ ∠ABD = ∠ACD (II)
In DABD, exterior ∠ADC = ∠ABD + ∠BAD
⇒ ∠ADC > ∠ABD
⇒ ∠ADC > ∠ACD [From (II)]
Now, in any triangle, the side opposite to the largest angle is the largest.
⇒ AC > AD
⇒ AB > AD [From (I)]
Solution 2
AD = AC (Given)
⇒ ΔADC is an isosceles triangle.
⇒ ∠ADC = ∠ACD = acute angle
Now, ∠ADC + ∠ADB = 180o [Linear pair]
⇒ ∠ADB is an obtuse angle.
Therefore, in ΔABD, ∠ADB is the largest angle.
Now, in any triangle, the side opposite to the largest angle is the largest.
⇒ AB > AD
Solution 3
The sum of the lengths of any two sides of a triangle is always greater than the third side.
In ΔPQS,
PQ + QS >PS (I)
In ΔPSR,
SR + RP >PS (II)
Adding equations (I) and (II),
PQ + QS + SR + RP > PS + PS
⇒ PQ + QR + RP >2PS (proved)
Solution 4
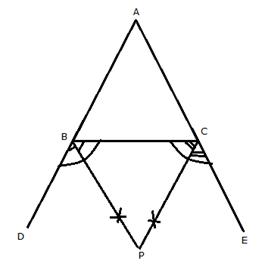
In ![]() ABC,
ABC,
AB > AC,
![]()
![]() ABC <
ABC < ![]() ACB
ACB
![]() 1800 -
1800 -![]() ABC > 1800 -
ABC > 1800 -![]() ACB
ACB

Solution 5
Since AB is the largest side and BC is the smallest side of the triangle ABC
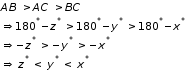
Solution 6
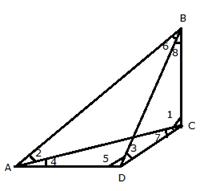
In the quad. ABCD,
Since AB is the longest side and DC is the shortest side.
(i) ![]() 1 >
1 > ![]() 2[AB > BC]
2[AB > BC]
![]() 7 >
7 > ![]() 4[AD > DC]
4[AD > DC]
![]()
![]() 1 +
1 + ![]() 7 >
7 > ![]() 2 +
2 + ![]() 4
4
![]()
![]() C >
C > ![]() A
A
(ii) ![]() 5 >
5 > ![]() 6[AB > AD]
6[AB > AD]
![]() 3 >
3 > ![]() 8[BC > CD]
8[BC > CD]
![]()
![]() 5 +
5 + ![]() 3 >
3 > ![]() 6 +
6 + ![]() 8
8
![]()
![]() D >
D > ![]() B
B
Solution 7
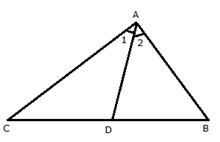
In ![]() ADC,
ADC,
![]() ADB =
ADB = ![]() 1 +
1 + ![]() C.............(i)
C.............(i)
In ![]() ADB,
ADB,
![]() ADC =
ADC = ![]() 2 +
2 + ![]() B.................(ii)
B.................(ii)
But AC > AB[Given]
![]()
![]() B >
B > ![]() C
C
Also given, ![]() 2 =
2 = ![]() 1[AD is bisector of
1[AD is bisector of ![]() A]
A]
![]()
![]() 2 +
2 + ![]() B >
B > ![]() 1 +
1 + ![]() C …….(iii)
C …….(iii)
From (i), (ii) and (iii)
![]()
![]() ADC >
ADC > ![]() ADB
ADB
Solution 8
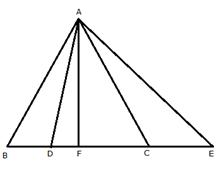
We know that the bisector of the angle at the vertex of an isosceles triangle bisects the base at right angle.
Using Pythagoras theorem in ![]() AFB,
AFB,
AB2 = AF2 + BF2…………..(i)
In ![]() AFD,
AFD,
AD2 = AF2 + DF2…………..(ii)
We know ABC is isosceles triangle and AB = AC
AC2 = AF2 + BF2 ……..(iii)[ From (i)]
Subtracting (ii) from (iii)
AC2 - AD2 = AF2 + BF2 - AF2 - DF2
AC2 - AD2 = BF2 - DF2
Let 2DF = BF
AC2 - AD2 = (2DF)2 - DF2
AC2 - AD2 = 4DF2 - DF2
AC2 = AD2 + 3DF2
![]() AC2 > AD2
AC2 > AD2
![]() AC > AD
AC > AD
Similarly, AE > AC and AE > AD.
Solution 9
The sum of any two sides of the triangle is always greater than the third side of the triangle.

Solution 10


