Class 9 SELINA Solutions Maths Chapter 27: Graphical Solution (Solution of Simultaneous Linear Equations, Graphically)
Graphical Solution (Solution of Simultaneous Linear Equations, Graphically) Exercise Ex. 27(A)
Solution 1(a)
Correct option: (i)10
Put x = k and y = 2 in the equation x - 4y = 2
∴ k - 4×2 = 2
∴ k = 10
Solution 1(b)
Correct option: (ii) 2
Put x = 5 and y = 2 in the equation y = mx - 8
∴2 = 5m - 8
∴ m = 2
Solution 1(c)
Correct option: (iii) (2 , 0)
Let the point be (x, 0)
Substituting in equation we get
∴5x -2(0) - 10 = 0
∴5x = 10
∴x = 2
∴ point is (2, 0)
Solution 1(d)
Correct option: (iv) (0 , -5)
Let the point be (0, y)
Substituting in equation we get
∴5(0) - 4y - 20 = 0
∴4y = -20
∴y = -5
∴ point is (0, -5)
Solution 1(e)
Correct option: (iv) x-axis and y-axis
Point (0,0) is the intersection of x and y axis, hence it lies on both x-axis and y-axis.
Solution 2
(i)
The graph x= 5 in the following figure is a straight line AB which is parallel to y axis at a distance of 5 units from it.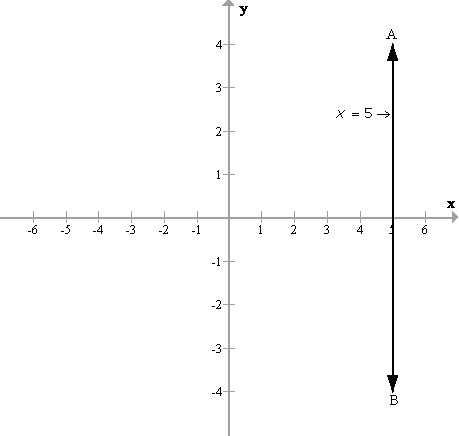
(ii)
x+5=0 Þx = -5
The graph x= -5 in the following figure is a straight line AB which is parallel to y axis at a distance of 5 units from it in the negative x direction.
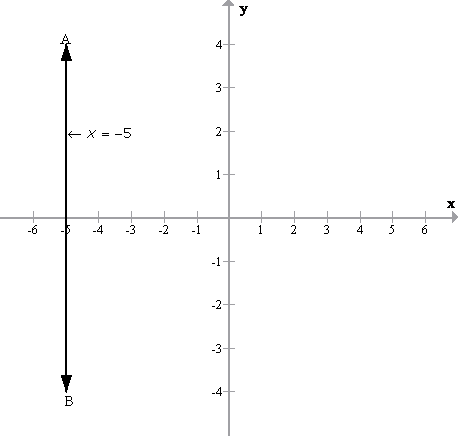
(iii)
The graph y = 7 in the following figure is a straight line AB which is parallel to x axis at a distance of 7 units from it.

(iv)
y+7=0 ![]() y = -7
y = -7
The graph y = -7 in the following figure is a straight line AB which is parallel to x axis at a distance of 7 units from it in the negative y direction.
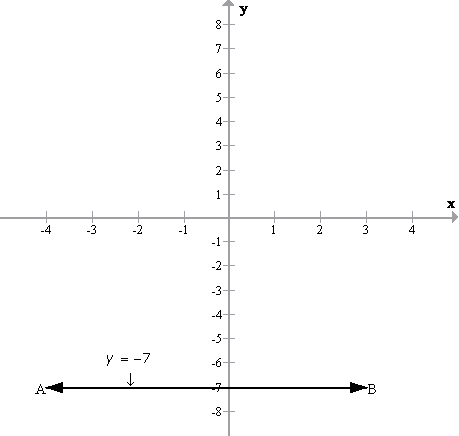
(v)
2x + 3y = 0
![]() 3y=-2x
3y=-2x


(vi)
3x + 2y = 6
![]() 2y=6-3x
2y=6-3x


(vii)
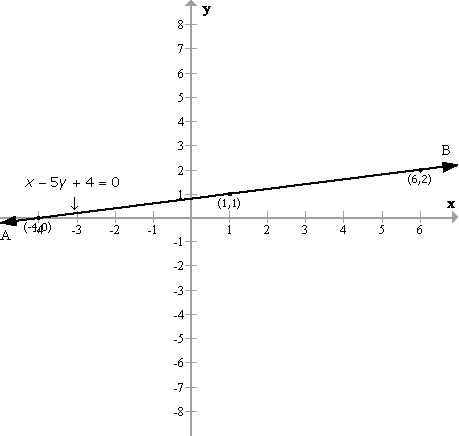
x-5y+4=0
![]() 5y=4+x
5y=4+x
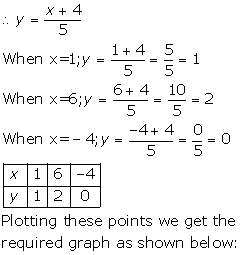
(viii)
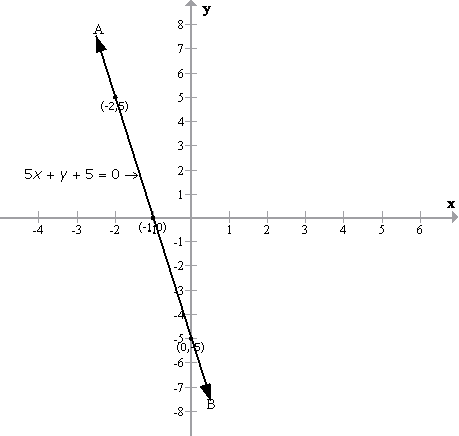
5x + y + 5 = 0
![]() y = -5x - 5
y = -5x - 5

Solution 3


From the figure it is clear that, the graph meets the coordinate
axes at (3, 0) and (0, 5)


From the figure it is clear that, the graph meets the coordinate axes at (-9, 0) and (0, 6)
Solution 4

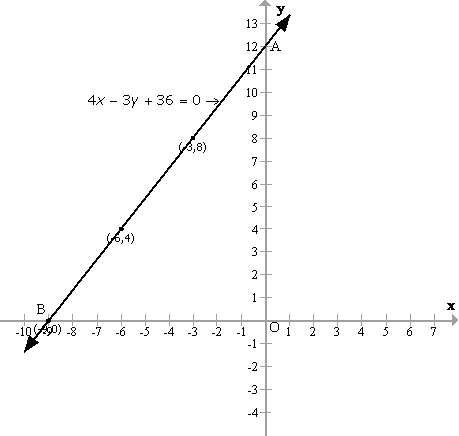
The straight line cuts the co-ordinate axis at A(0, 12) andB(-9, 0).
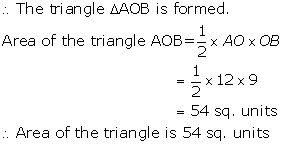
Solution 5

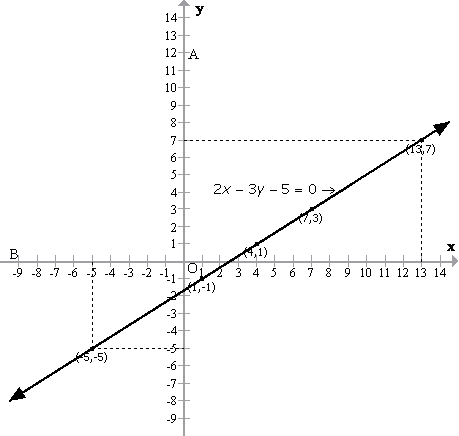
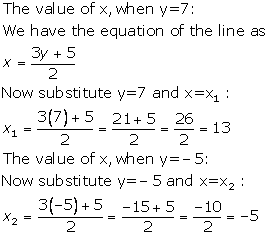
Solution 6

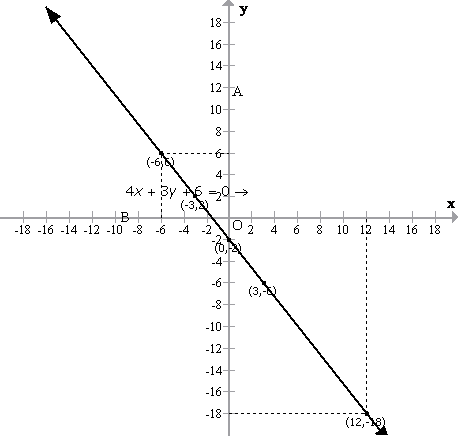

Solution 7

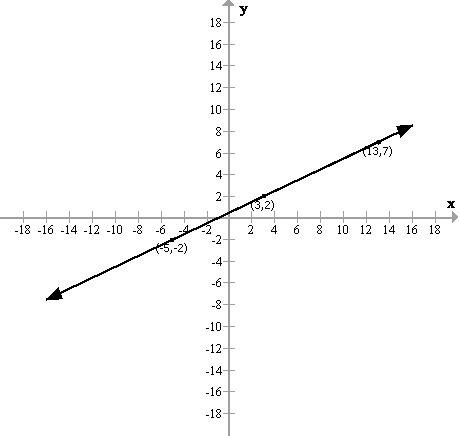
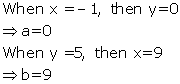
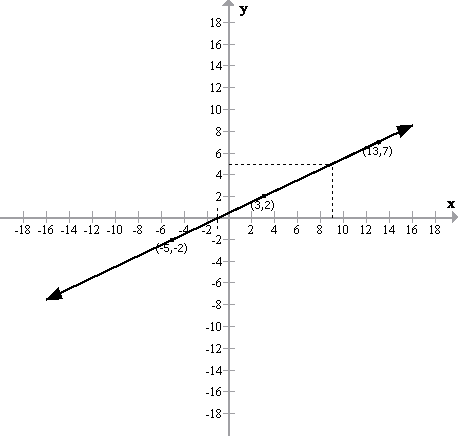

Solution 8
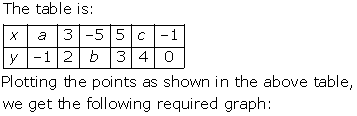
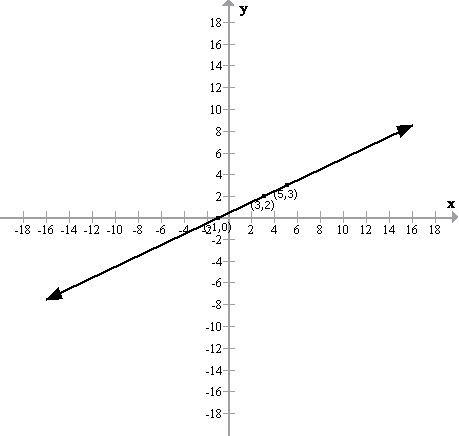
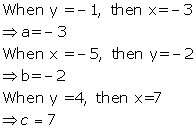

Solution 9

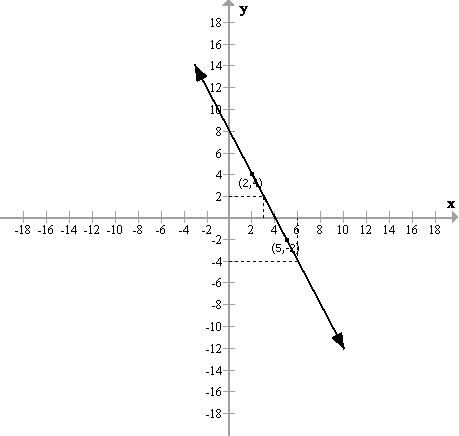

Solution 10
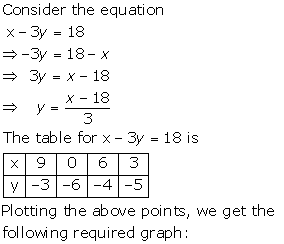

![]()
Graphical Solution (Solution of Simultaneous Linear Equations, Graphically) Exercise Ex. 27(B)
Solution 1(a)
Correct option: (i) (8, 8)
x = 8
y - 8 = 0
∴ y = 8
So the point of intersection is (8, 8)
Solution 1(b)
Correct option: (ii) 60
y = 20 + 2x
substitute x = 20, we get
y = 20 + 2(20)
∴ y = 60
Solution 1(c)
Correct option: (iii) (5, 2)
Point lying on the line 2x - 3y = 4, should satisfy the line's equation.
On substituting x = 5 and y = 2
We get,
2(5) - 3(2) = 4
4 = 4
Hence, LHS = RHS
∴ (5, 2) lies on the line 2x - 3y = 4
Solution 1(d)
Correct option: (ii) is parallel to y-axis
x + 5 = 0
∴ x = -5
Hence, the line is parallel to y-axis
Solution 1(e)
Correct option: (iv) (3, 2)
y - 2 = 0
∴ y = 2 …substitute in 2x + 3y =12
We get,
2x + 6 = 12
∴ x = 3
Hence, the point is (3, 2)
Solution 2
(i)
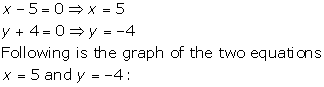
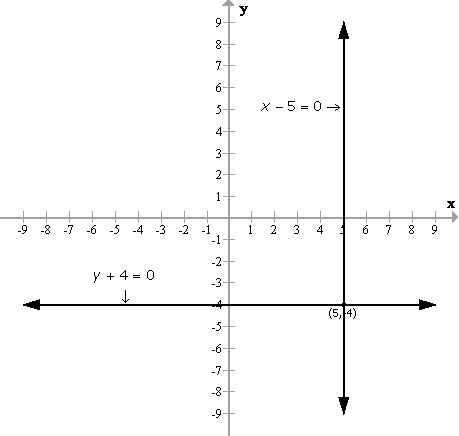
(ii)


(iii)

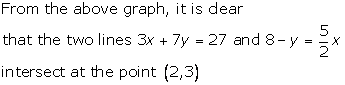
(iv)

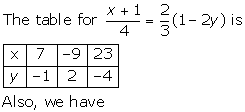

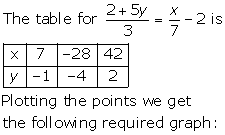
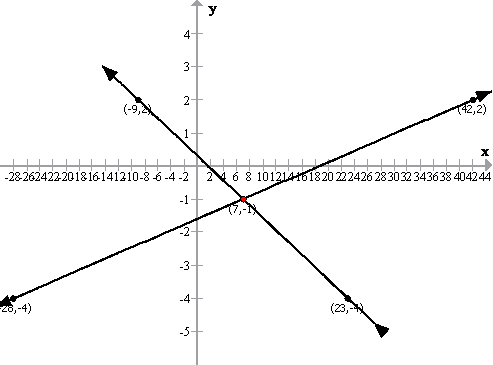
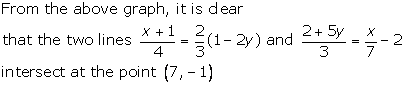
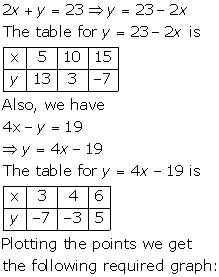
Solution 3
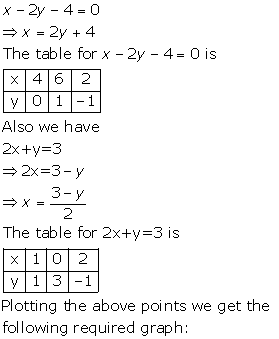
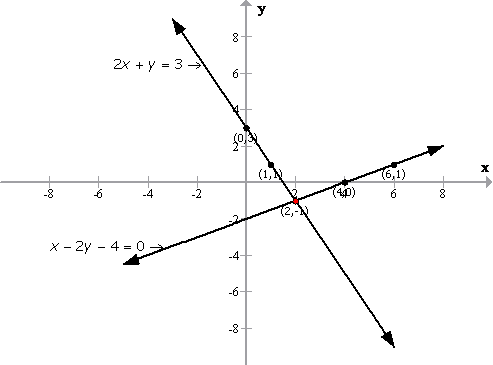
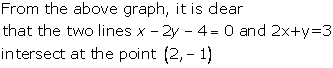
Solution 4
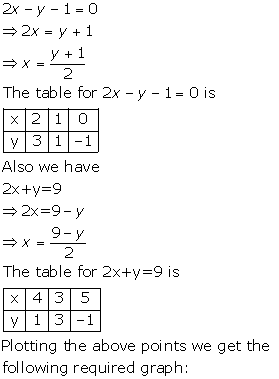
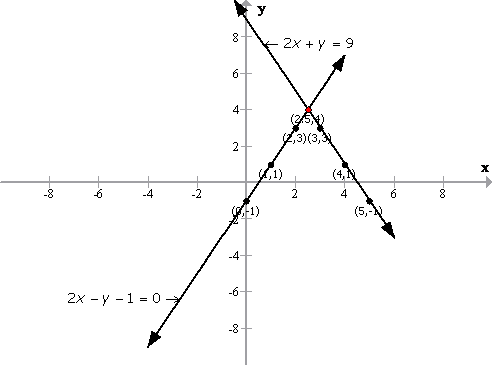
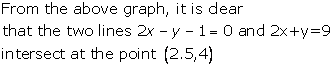
Solution 5


Solution 6
(i)

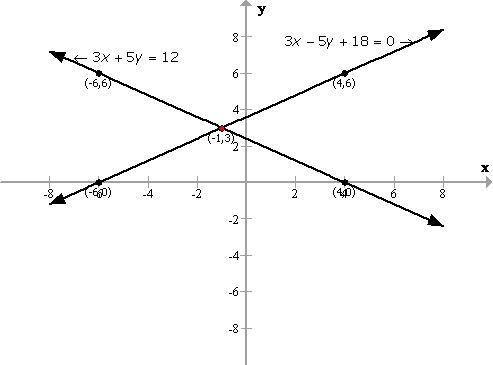
(ii)
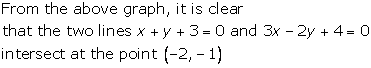
(iii)

Solution 7

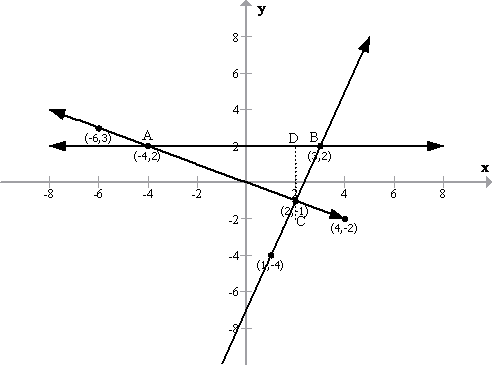
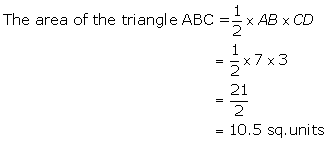
(ii)
![]()
Solution 8
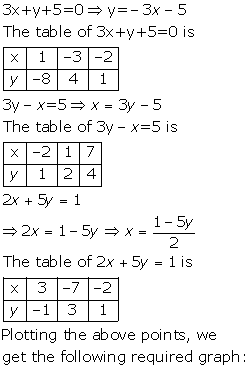
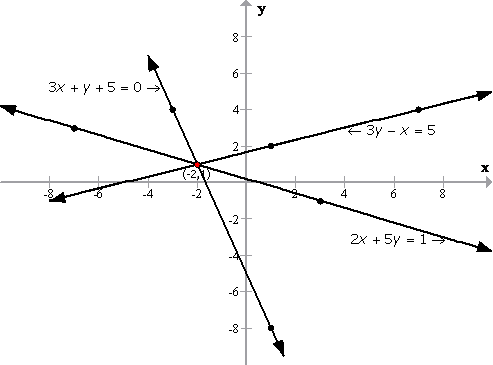
![]()
Solution 9

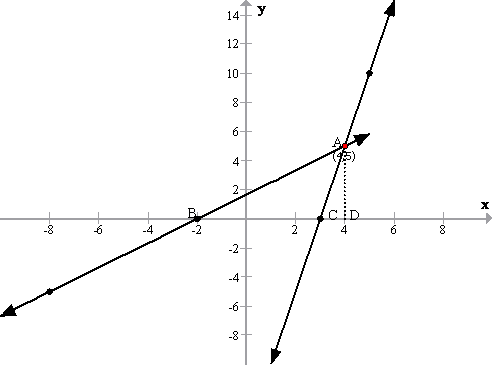
(i)

(ii)
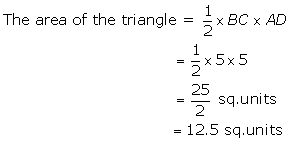
Solution 10

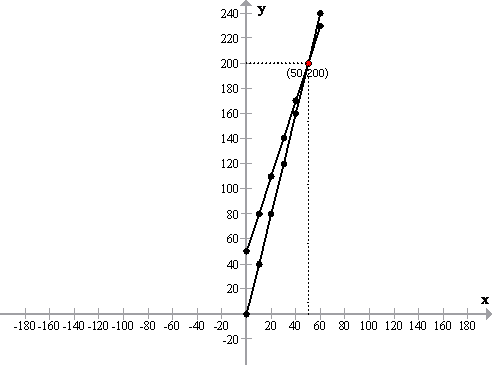
(i)
No. of articles to be manufactured and sold are 50 when there is no loss and no profit.
C.P = S.P = Rs.200
(ii)
(a)
On article 30,
C.P = Rs.140 and S.P. = 120
Therefore Loss = 140 - 120 = Rs.20
(b)
On article 60,
C.P.=Rs.230 and S.P.= Rs.240
Therefore Profit = 240 - 230 = Rs.10
Graphical Solution (Solution of Simultaneous Linear Equations, Graphically) Exercise Test Yourself
Solution 1
Distance of a point from y-axis is equal to the absolute value of its x co-ordinate.
Hence, the distance will be 8 units.
Solution 2
Scale: 1cm = 1 unit on both axis
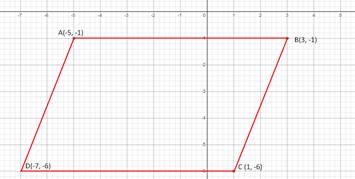
Solution 3
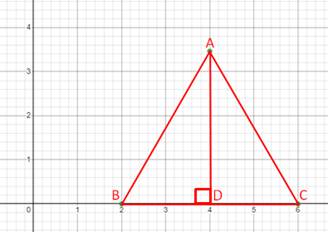
Length BC = 6 - 2 = 4 units,
As it is equilateral triangle, AB = 4 units.
Draw a perpendicular from A to BC.
Hence, BD = DC = 2 units
Now ∆ABD is right angled
Hence,
AB2 = AD2 + BD2

Solution 4
Scale: 1cm = 1 units on both axes
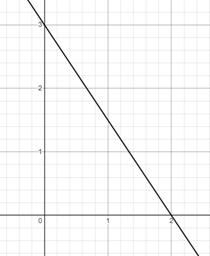
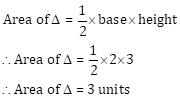
Solution 5
(i)
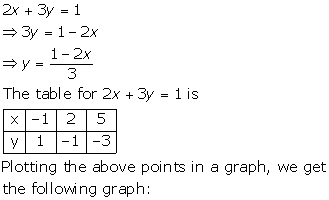

![]()
(ii)
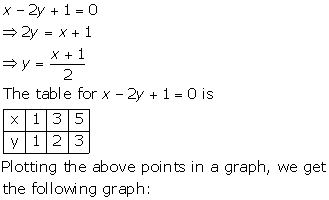
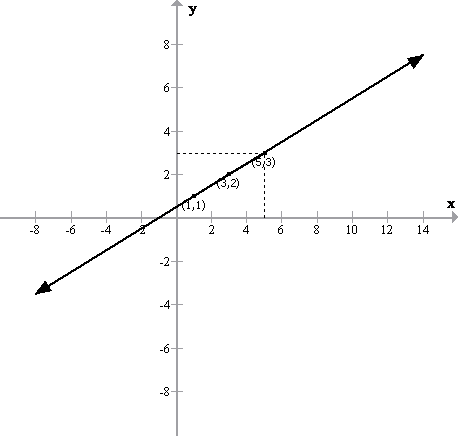
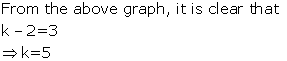
Solution 6
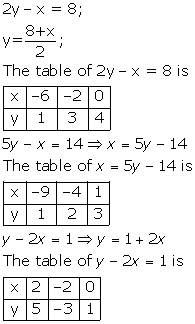
![]()

![]()
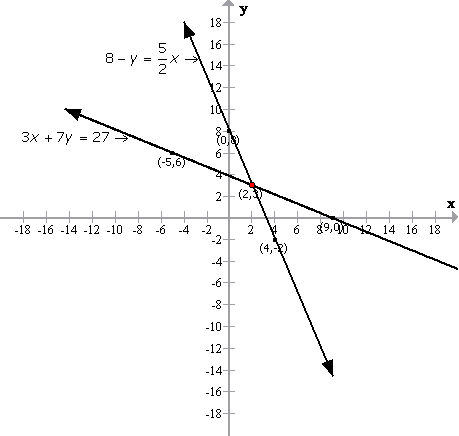
Solution 7
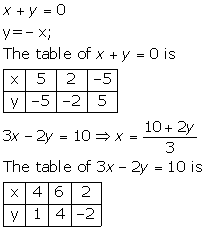
![]()
![]()
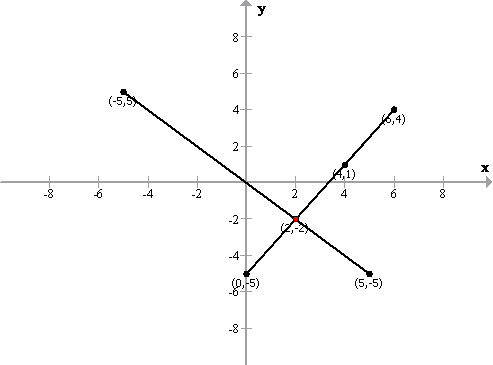
Solution 8
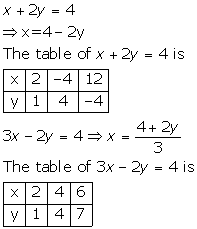
![]()
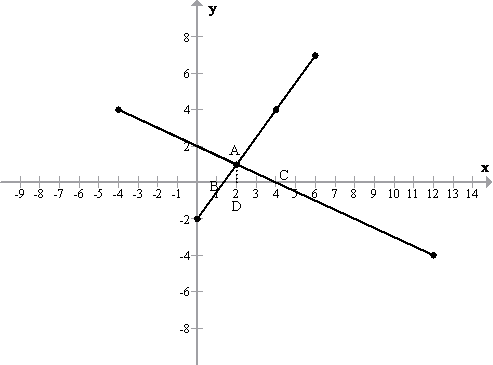
Therefore the solution of the given system of equations is (2,1).

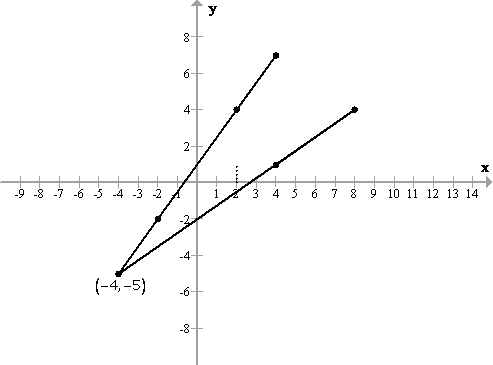
Solution 9
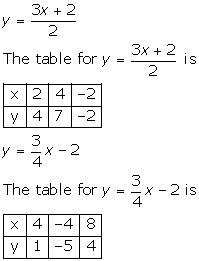
![]()
![]()
Solution 10
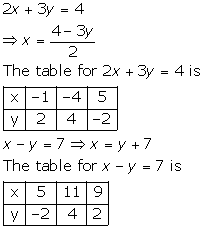
![]()
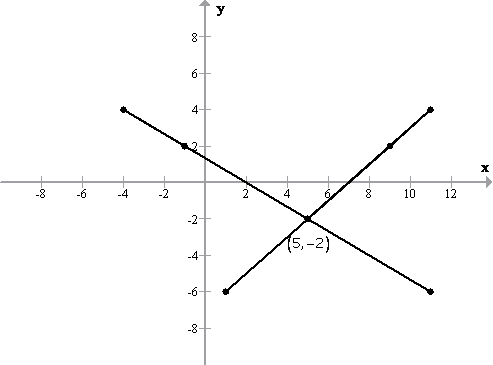
![]()
