Class 9 SELINA Solutions Maths Chapter 5: Factorisation
Factorisation Exercise Ex. 5(A)
Solution 1(a)
Correct option: (i) ![]()
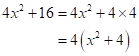
Solution 1(b)
Correct option:
(iii) ![]()
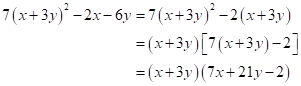
Solution 1(c)
Correct option:
(iii) ![]()
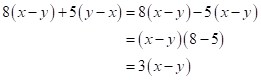
Solution 1(d)
Correct option: (iv)
![]()
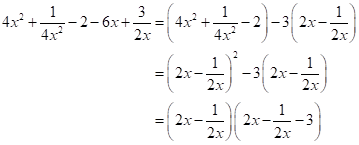
Solution 1(e)
Correct option:
(ii) ![]()
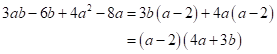
Solution 2
2(2x - 5y)(3x + 4y) - 6(2x - 5y)(x - y)
Taking (2x - 5y) common from both terms
= (2x - 5y)[2(3x + 4y) - 6(x - y)]
=(2x - 5y)(6x + 8y - 6x + 6y)
=(2x - 5y)(8y + 6y)
=(2x - 5y)(14y)
=(2x - 5y)14y
Solution 3
xy(3x2 - 2y2) - yz(2y2 - 3x2) + zx(15x2 - 10y2)
= xy(3x2 - 2y2) + yz(3x2 - 2y2) + zx(15x2 - 10y2)
= xy(3x2 - 2y2) + yz(3x2 - 2y2) + 5zx(3x2 - 2y2)
= (3x2 - 2y2)[xy + yz + 5zx]
Solution 4
ab(a2 + b2 - c2) - bc(c2 - a2 - b2) + ca(a2 + b2 - c2)
= ab(a2 + b2 - c2) + bc(a2 + b2 - c2) + ca(a2 + b2 - c2)
= (a2 + b2 - c2)[ab + bc + ca]
Solution 5
2x(a - b) + 3y(5a - 5b) + 4z(2b - 2a)
= 2x(a - b) + 15y(a - b) - 8z(a - b)
= (a - b)[2x + 15y - 8z]
Solution 6
a3 + a - 3a2 - 3= a (a2 + 1) - 3(a2 + 1)
= (a2 + 1) (a -3).
Solution 7
16 (a + b)2 - 4a - 4b =16 (a + b)2 - 4 (a + b)
= 4 (a + b) [4 (a + b) - 1]
= 4 (a + b) (4a + 4b - 1)
Solution 8
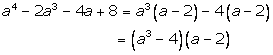
Solution 9
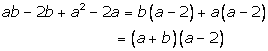
Solution 10
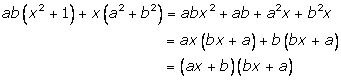
Solution 11
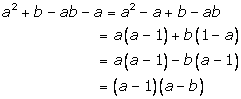
Solution 12

Solution 13
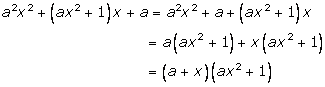
Solution 14
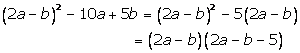
Solution 15
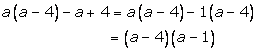
Solution 16
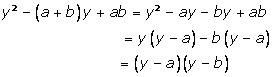
Factorisation Exercise Ex. 5(B)
Solution 1(a)
Correct option:
(iii) ![]()
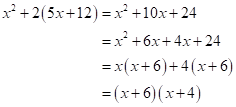
Solution 1(b)
Correct option:
(iv) ![]()
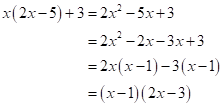
Solution 1(c)
Correct option:
(ii) ![]()
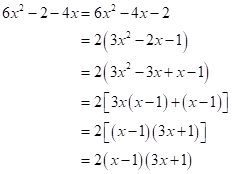
Solution 1(d)
Correct option: (i) ![]()
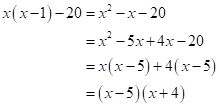
Solution 1(e)
Correct option:
(iii) ![]()
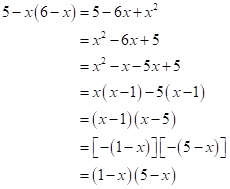
Solution 2
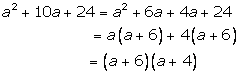
Solution 3
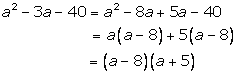
Solution 4
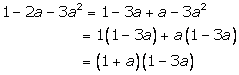
Solution 5
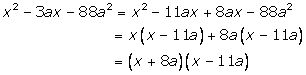
Solution 6
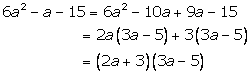
Solution 7
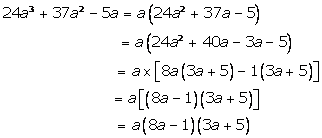
Solution 8
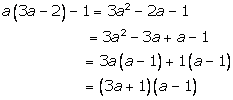
Solution 9
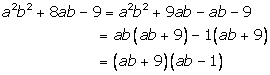
Solution 10

Solution 11

Solution 12
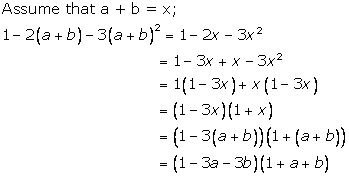
Solution 13
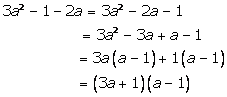
Solution 14
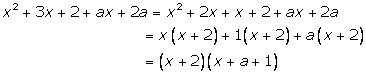
Solution 15
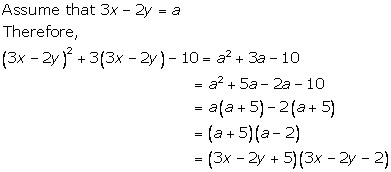
Solution 16

Factorisation Exercise Ex. 5(C)
Solution 1(a)
Correct option:
(ii) ![]()
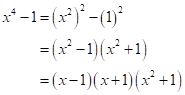
Solution 1(b)
Correct option: (i) ![]()
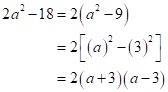
Solution 1(c)
Correct option:
(iv) ![]()
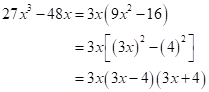
Solution 1(d)
Correct option: (i) ![]()
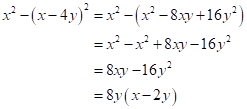
Solution 1(e)
Correct option: (i) ![]()
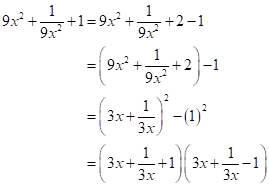
Solution 2
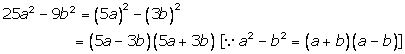
Solution 3
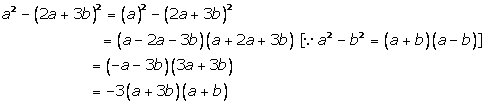
Solution 4
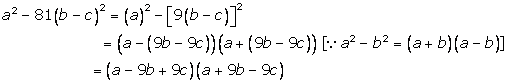
Solution 5

Solution 6

Solution 7
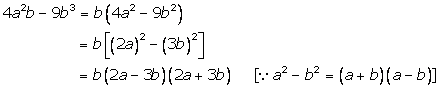
Solution 8
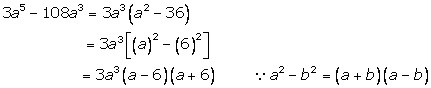
Solution 9

Solution 10
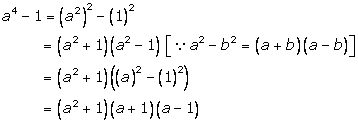
Solution 11
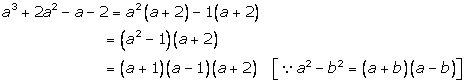
Solution 12

Solution 13
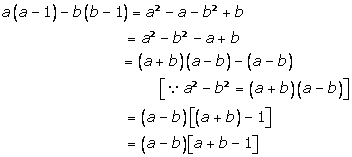
Solution 14
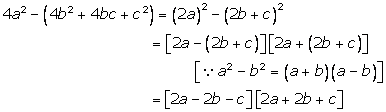
Solution 15
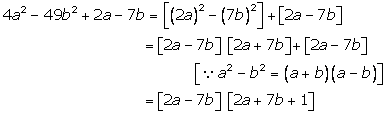
Solution 16
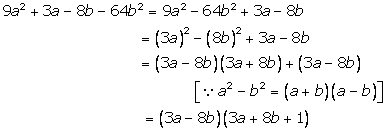
Solution 17
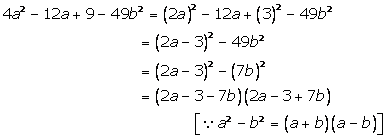
Solution 18
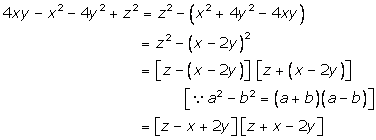
Solution 19
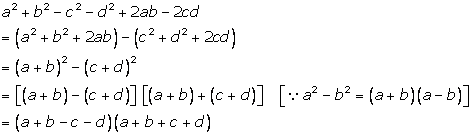
Solution 20

Solution 21

Solution 22
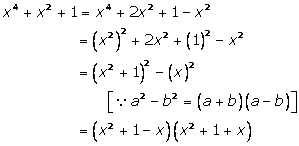
Solution 23
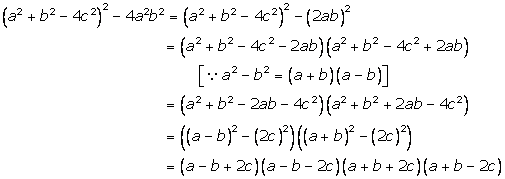
Solution 24

Solution 25
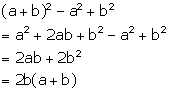
Solution 26
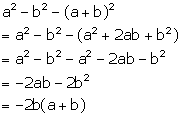
Factorisation Exercise Ex. 5(D)
Solution 1(a)
Correct option:
(ii) ![]()
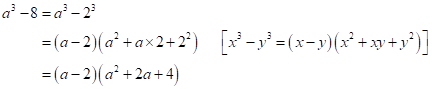
Solution 1(b)
Correct option: (iii)
![]()
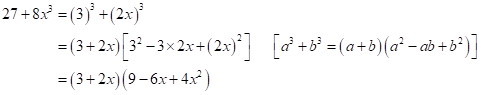
Solution 1(c)
Correct option: (i) ![]()
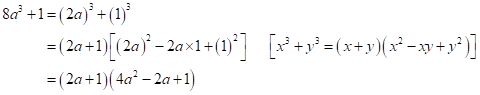
Solution 1(d)
Correct option:
(iii) 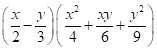
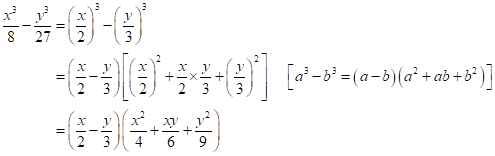
Solution 2

Solution 3
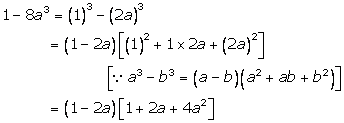
Solution 4
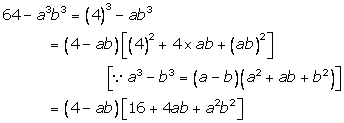
Solution 5
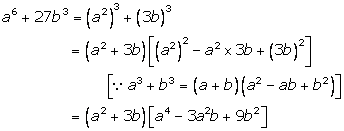
Solution 6

Solution 7
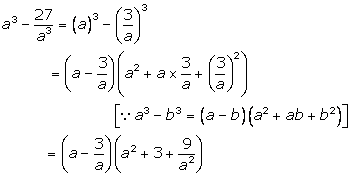
Solution 8
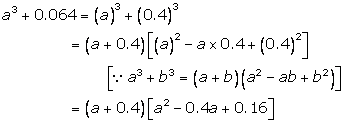
Solution 9
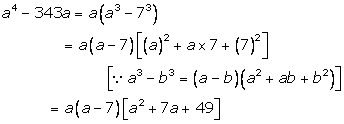
Solution 10
(x - y)3 - 8x3
= (x - y)3 - (2x)3
= (x - y - 2x)[(x - y)2 + 2x(x - y) + (2x)2]
[Using identity (a3 - b3) = (a - b)(a2 + ab + b2)]
= (-x - y)[x2 + y2 - 2xy + 2x2 - 2xy + 4x2]
= -(x + y) [7x2 - 4xy + y2]
Solution 11
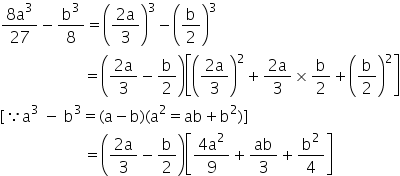
Solution 12

Solution 13

Solution 14

Solution 15

Solution 16
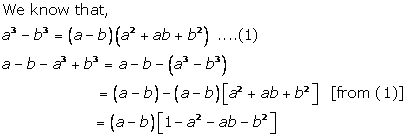
Factorisation Exercise Ex. 5(E)
Solution 1(a)
Correct option:
(ii) ![]()
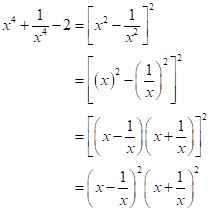
Solution 1(b)
Correct option: (iv)
![]()
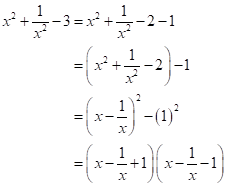
Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
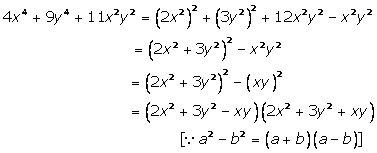
Solution 7

Solution 8

Solution 9
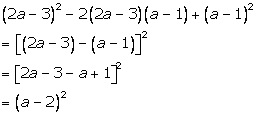
Solution 10

Solution 11
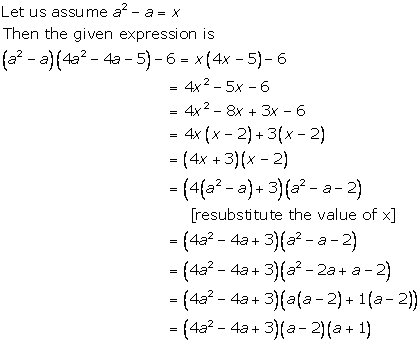
Solution 12
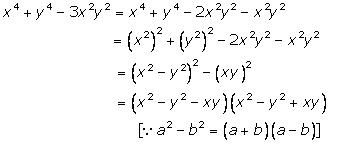
Solution 13

Solution 14

Solution 15

Solution 16

Factorisation Exercise Test Yourself
Solution 1
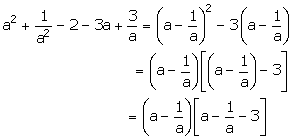
Solution 2
x2 + y2 + x + y + 2xy
= (x2 + y2 + 2xy ) + (x + y) [As (x + y)2 = x2 + 2xy + y2]
=(x + y)2 + (x + y)
=(x + y)(x + y + 1)
Solution 3
a2 + 4b2 - 3a + 6b - 4ab
= a2 + 4b2 - 4ab - 3a + 6b
= a2 + (2b)2 - 2 × a × (2b) - 3(a - 2b) [As (a - b)2 = a2 - 2ab + b2 ]
= (a - 2b)2 - 3(a - 2b)
= (a - 2b)[(a - 2b)- 3]
= (a - 2b)(a - 2b - 3)
Solution 4
m (x - 3y)2 + n (3y - x) + 5x - 15y
= m (x - 3y)2 - n (x - 3y) + 5(x - 3y)
[Taking (x - 3y) common from all the three terms]
= (x - 3y) [m(x - 3y) - n + 5]
= (x - 3y)(mx - 3my - n + 5)
Solution 5
x (6x - 5y) - 4 (6x - 5y)2
= (6x - 5y)[x - 4(6x - 5y)]
[Taking (6x - 5y) common from the three terms]
= (6x - 5y)(x - 24x + 20y)
= (6x - 5y)(-23x + 20y)
= (6x - 5y)(20y - 23x)
Solution 6
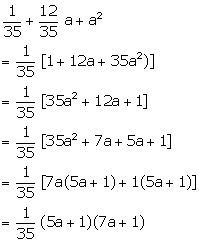
Solution 7
(x2 - 3x)(x2 - 3x - 1) - 20
= (x2 - 3x)[(x2 - 3x) - 1] - 20
= a[a - 1] - 20 ….(Taking x2 - 3x = a)
= a2 - a - 20
= a2 - 5a + 4a - 20
= a(a - 5) + 4(a - 5)
= (a - 5)(a + 4)
= (x2 - 3x - 5)(x2 - 3x + 4)
Solution 8
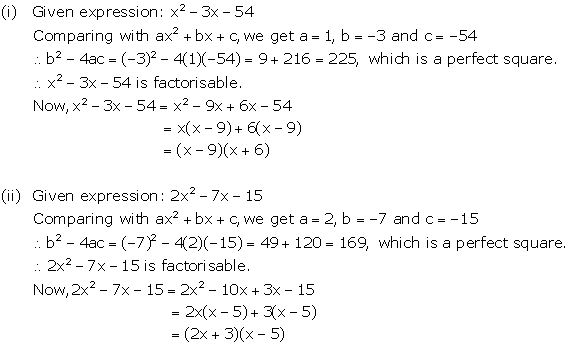
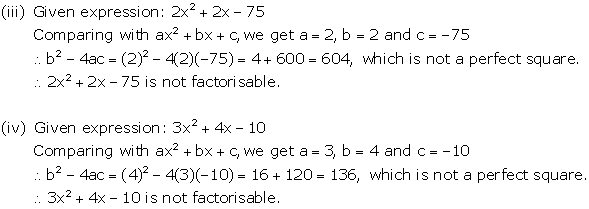
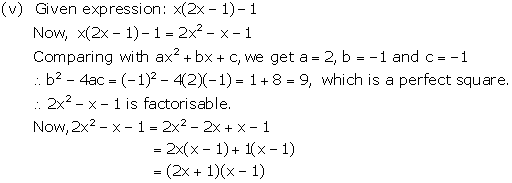
Solution 9
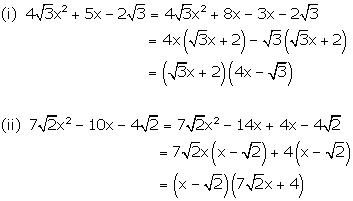
Solution 10
12x2 - 35x + 25
= 12x2 - 20x - 15x + 25
= 4x(3x - 5) - 5(3x - 5)
= (3x - 5)(4x - 5)
Thus,
Length = (3x - 5) and breadth = (4x - 5)
OR
Length = (4x - 5) and breadth = (3x - 5)
Solution 11
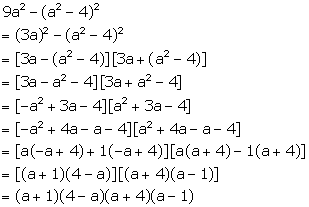
Solution 12

Solution 13

Solution 14
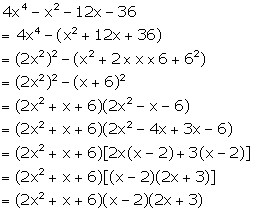
Solution 15
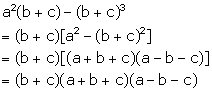
Solution 16
2x3 + 54y3 - 4x - 12y
= 2(x3 + 27y3 - 2x - 6y)
= 2{[(x)3+(3y)3] - 2(x + 3y)} [Using identity (a3 + b3) = (a + b)(a2 - ab + b2)]
= 2{[(x + 3y)(x2 - 3xy + 9y2)] - 2(x + 3y)}
= 2(x + 3y)(x2 - 3xy + 9y2 - 2)
Solution 17
1029 - 3x3
= 3(343 - x3)
= 3(73 - x3)
= 3(7 - x)(72 + 7x + x2)
= 3(7 - x)(49 + 7x + x2)
Solution 18
(i) (133 - 53)
[Using identity (a3 - b3) = (a - b)(a2 + ab + b2)]
= (13 - 5)(132 + 13 × 5 + 52)
= 8(169 + 65 + 25)
Therefore, the number is divisible by 8.
(ii) (353 + 273)
[Using identity (a3 + b3)=(a + b)(a2 - ab + b2)]
= (35 + 27)(352 + 35× 27 + 272)
= 62 × (352 + 35 × 27 + 272)
Therefore, the number is divisible by 62.
Solution 19

Solution 20
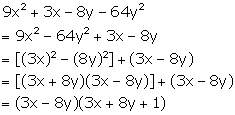
Solution 21

Solution 22

Solution 23
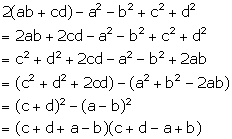
Solution 24

